Code
set.seed(112358)
r <- rnorm(n=10000, mean=0.0975, sd=0.18)
P0 <- 1000
P1 <- P0*(1+r)The best way to learn simulation is through an example.
Suppose you want to invest $1,000 (call this \(P_0\)) in the US stock market for one year. You invest in a mutual fund that tries to produce the same return as the S&P500 Index. Let’s keep this example basic and only work with annual return. The price after one year can be calculated as follows:
\[ P_1 = P_0 \times (1 + r_{0,1}) \]
The term \(r_{0,1}\) refers to the annual return from time point 0 to time point 1. Let’s assume annual returns follow a Normal distribution with a historical mean of 9.75% and a standard deviation of 18%.
Let’s see how we would simulate this problem in each of our software!
Simulation is rather easy to do in R because R is a vector language. This makes it so you don’t have to use as many loops as in other languages. This is easily seen in this example. We start by setting a seed with the set.seed function so we can replicate our results. We then just use the rnorm function to randomly generate the possible values of the one year annual return. The n = option tells R the number of random draws you would like from the distribution. The mean = and sd = options define the mean and standard deviation of the normal distribution respectively. This creates a vector of observations. With R’s ability to do vector math, we can just add 1 to every element in the vector and multiply that by our initial investment value defined as the P0 object below.
Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the summary function to calculate some summary statistics around our distribution of possible values of our portfolio after one year. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of P1, the values of our portfolio after one year.

Not surprisingly, we can see that a majority of the values are above our initial investment of $1,000. In fact, on average, we would expect to make 9.75% return as that is the mean of our normal distribution. However, there is a spread to our returns as well so not all returns are above our initial investment. We can see there are a portion of scenarios that have us fall below our initial investment value.
Simulation is rather easy to do in Python because Python is a vector language. In this example we are going to use loops to quickly simulate through our example. We start by setting a seed with the random.seed function from numpy so we can replicate our results. We then just use the random.normal function from numpy to randomly generate the possible values of the one year annual return. The for loop tells Python the number of random draws you would like from the distribution. The loc = and scale = options define the mean and standard deviation of the normal distribution respectively. This creates a vector of observations as we append the values on the end of each other as we loop through. As we go, we can just add 1 to every element in the vector and multiply that by our initial investment value defined as the P0 object below.
Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the describe function to calculate some summary statistics around our distribution of possible values of our portfolio after one year. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of P1, the values of our portfolio after one year using the histplot from seaborn.
0
count 10000.000000
mean 1096.649930
std 179.624575
min 460.595108
25% 975.377881
50% 1096.963413
75% 1215.218548
max 1761.824533
Not surprisingly, we can see that a majority of the values are above our initial investment of $1,000. In fact, on average, we would expect to make 9.75% return as that is the mean of our normal distribution. However, there is a spread to our returns as well so not all returns are above our initial investment. We can see there are a portion of scenarios that have us fall below our initial investment value.
Simulations in SAS highly depend on the DATA step. This is easily seen in this example. We start by creating a new data set called SPIndex using the DATA step. We then use a do loop. Here we want to loop across the values of i from 1 to 10,000. We set up our initial investment value as P0 and define r as the return. We use the RAND function to draw a random value for our returns. This random value comes from the options specified in the RAND function. Here we specify that we want a 'Normal' distribution with a mean of 0.0975 and standard deviation of 0.18. We then calculate the portfolio value after 1 year and call it P1. The OUTPUT statement saves this calculation and moves to the next step in the loop. The END statement defines the end of the loop.

Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the PROC MEANS procedure to calculate some summary statistics around our distribution of possible values of our portfolio after one year. We use the DATA = option to define the dataset of interest and the VAR statement to define the variable we are interested in summarizing, here P1. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of P1, the values of our portfolio after one year, using PROC SGPLOT and the HISTOGRAM statement for P1.

Not surprisingly, we can see that a majority of the values are above our initial investment of $1,000. In fact, on average, we would expect to make 9.75% return as that is the mean of our normal distribution. However, there is a spread to our returns as well so not all returns are above our initial investment. We can see there are a portion of scenarios that have us fall below our initial investment value.
How did we select the normal distribution for our returns? Is that a good guess of a distribution? That we will need to find out in our next section.
When designing your simulations, the biggest choice comes from the decision of the distribution on the inputs that vary. There are 3 common methods for selecting these distributions:
Common Probability Distribution
Historical (Empirical) Distribution
Hypothesized Future Distribution
Typically, we assume a common probability distribution for inputs that vary in a simulation. We did this in our above example where we just assumed returns followed a normal distribution. When selecting distributions, we need to first decide if our variables are discrete or continuous in nature. A discrete variable take on outcomes that you can list out (even if you can not list all of them). Continuous variables on the other hand take on any possible value in a interval (even if the interval is unbounded).
Some commonly used discrete distributions for simulations are the following:
Uniform distribution
Poisson distribution
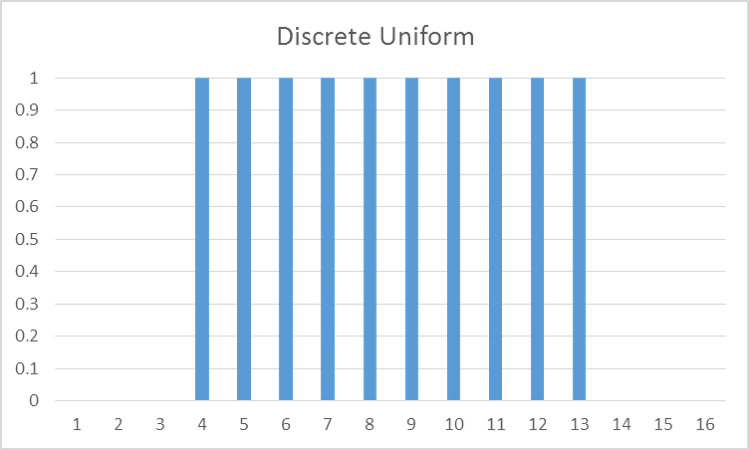
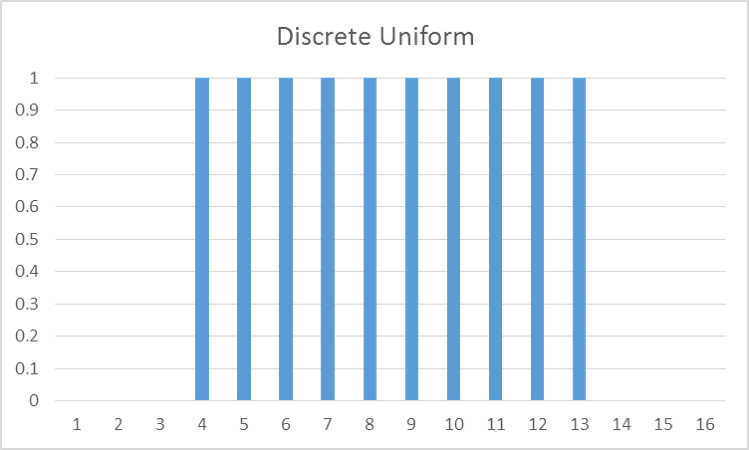
In the discrete uniform, every discrete value of the distribution has an equal probability of occurring.
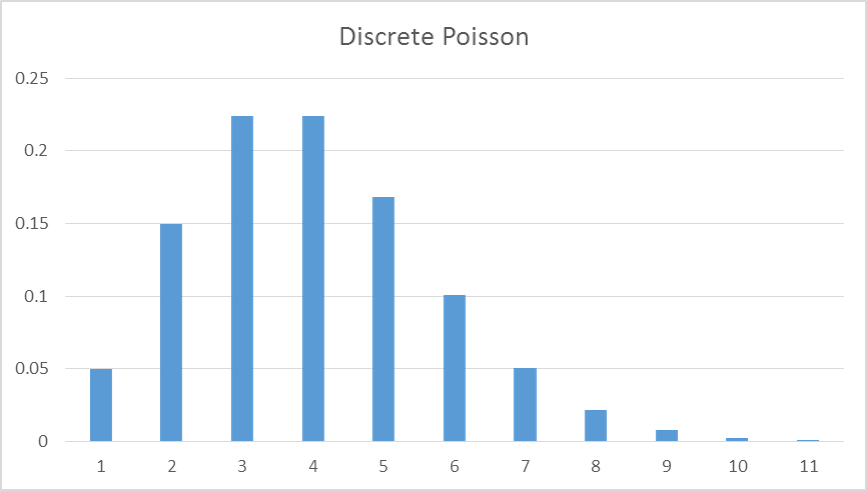
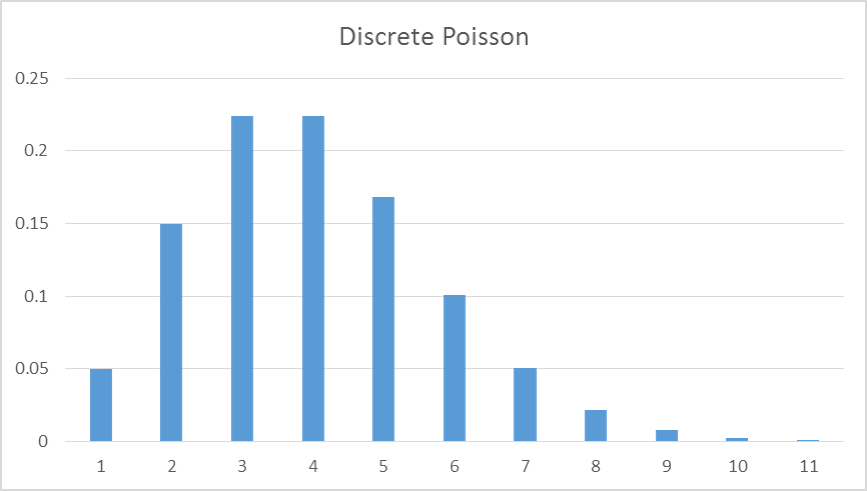
The Poisson distribution is best used for when you are counting events. It is bounded below by 0 and takes on all non-negative integer values with differing probabilities of occurrences based on the location of the distribution.
Some commonly used continuous distributions for simulations are the following:
Uniform distribution
Triangle distribution
Normal distribution
Student’s t-distribution
Lognormal distribution
Exponential distribution
Beta distribution
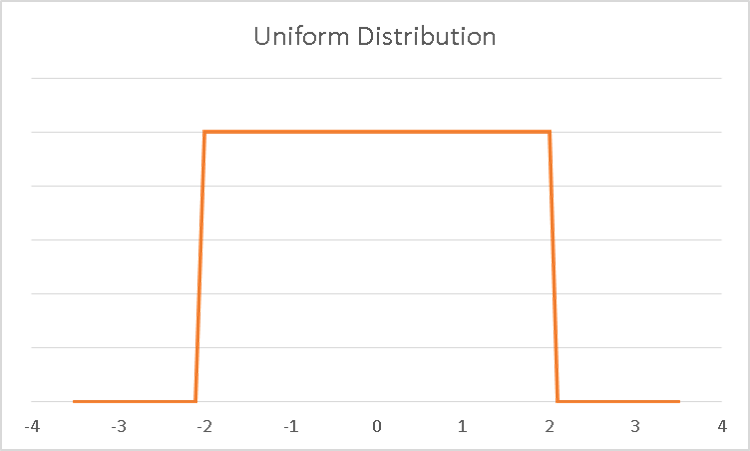
Much like its discrete counterpart, in the continuous uniform distribution every value of the distribution has an equal probability of occurring.

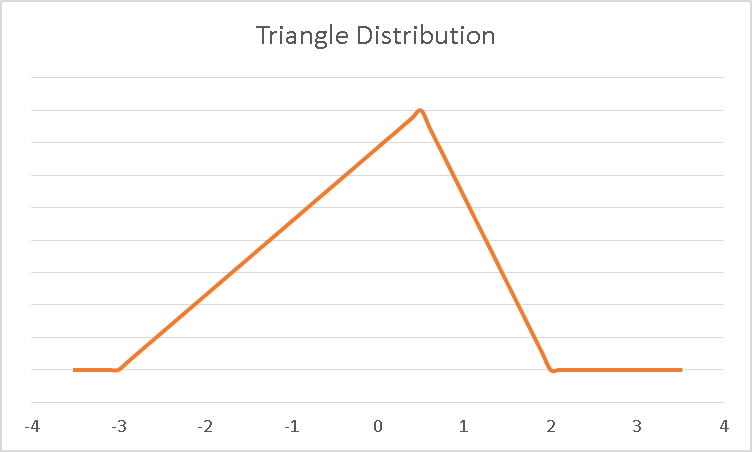
The triangle distribution is a great distribution for business scenarios where individuals might only be able to tell you three things - the worst case scenario, the best case scenario, and the most likely (in the middle) scenario. With these three points we can define the triangle distribution.
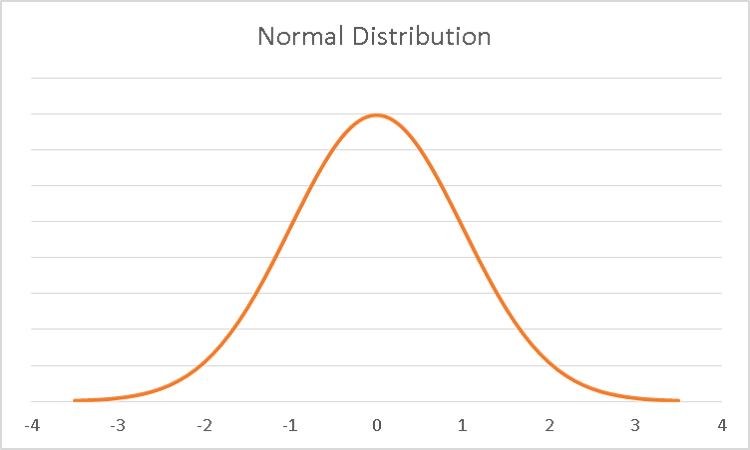
The Gaussian (normal) distribution is one of the most popular distributions out there. Bell-shaped and symmetric with nice mathematical properties, the normal distribution is used for inputs in many simulations.
The student’s t-distribution is bell-shaped and symmetric like the normal distribution, but it has thicker tails. This allows for more variability than the normal distribution provides.

The lognormal distribution is very popular in the financial simulation world as it has nice asymmetric properties which stock returns sometimes follow.

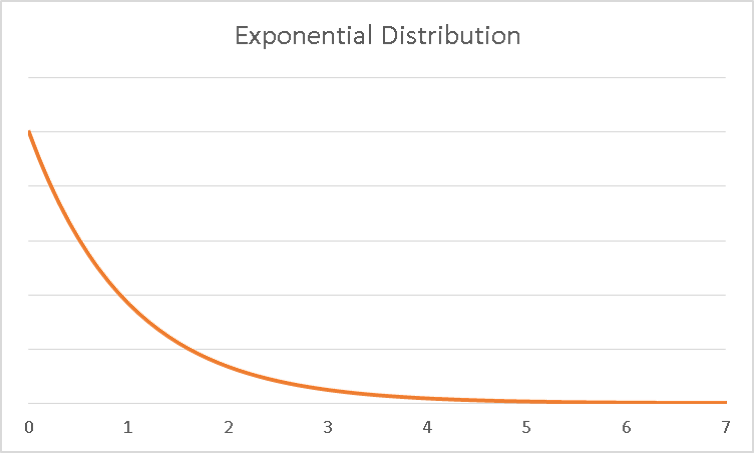
The exponential distribution is great for simulating risky (sometimes called tail) events. It is one of many distributions like it used in Extreme Value Theory.
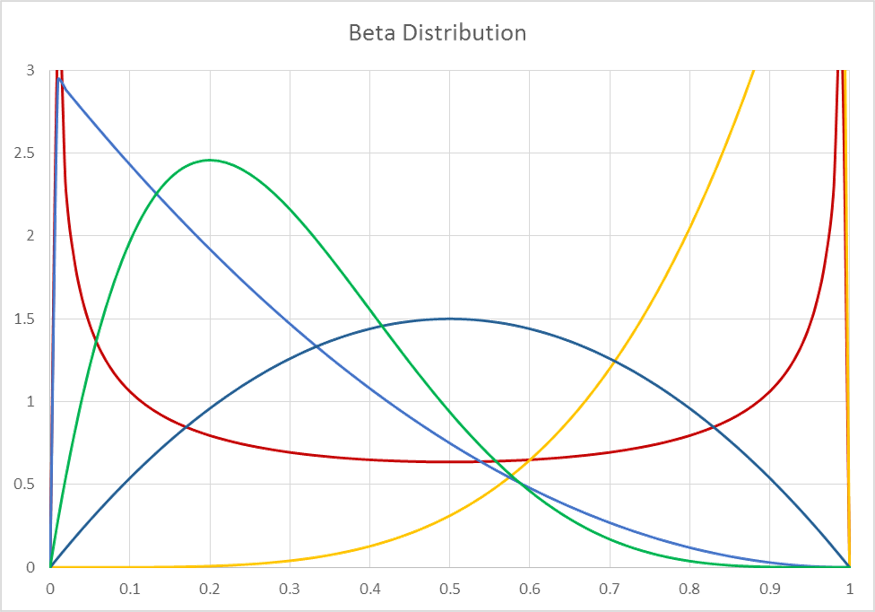
The Beta distribution is a family of distributions that take many shapes. Some of the most popular shapes in terms of simulations are the “bathtub” like shape that has higher probabilities of edge cases happening as compared to the middle cases.
If you are unsure of the distribution of the data you are trying to simulate, you can estimate it using the process of kernel density estimation. Kernel density estimation is a non-parametric method of estimating distributions of data through smoothing out of data values.
The kernel density estimator is as follows:
\[ \hat{f(x)} = \frac{1}{n\times h} \sum_{i=1}^n \kappa (\frac{x - x_i}{h}) \]
In the above equation \(\kappa\) is the kernel function. The kernel function builds a distribution centered around each of the points in your dataset. Imagine a small normal distribution built around each point and then adding these normal distributions together to form one larger distribution. The default kernel function distribution in a lot of software is the normal distribution, but there are other options like the quadratic, triangle, and Epanechnikov. The In the above equation \(h\) is the bandwidth. The bandwidth controls the variability around each point. The larger the variability, the more variation is built around each point through the distribution as seen in the chart below:

The above plot shows kernel density estimates of data sampled from a standard normal distribution. The actual distribution is highlighted with the dashed line above. Three estimates with different bandwidths are shown. The smaller the bandwidth, the smaller the variability around each point, but also the more highly fit our curve is to our data. The larger the bandwidth, the more variability around each point which smooths out the curve much more. We want to find the balance. There is a lot of research that has been done and still ongoing on how to best select bandwidth. We will leave it up to the computer to optimize this decision for us.
Once we have this kernel density estimate for our data, we can sample from this estimated distribution for our simulation. In our previous example we assumed a normal distribution for our returns of our mutual fund. Now, let’s build an empirical distribution through kernel density estimation and sample from that instead of the normal distribution.
Let’s see how to do this in each of our software!
Kernel density estimation can only happen when you have data to estimate a distribution on. First, we need to collect historical data on the S&P500 Index. We can do this through the getSymbols function in R. By putting in the stock ticker as it appears in the New York Stock Exchange, we can pull data from Yahoo Finance through this function. The ticker for the S&P500 Index is ^GSPC. The getSymbols function then gets us historical, daily opening prices, closing prices, high prices, and low prices all the way back to 2007. We want to calculate the annual return on the closing prices for the S&P500 Index. We can use the periodReturn function in R on the GSPC.Close column of the GSPC object created from the getSymbols function. The period = option defines the period you want to calculate returns on. We want yearly returns. We then plot a histogram of the data.
[1] "GSPC"
Next we need to use the density function in R to estimate the bandwidth for the kernel density estimation.
Call:
density.default(x = gspc_r)
Data: gspc_r (19 obs.); Bandwidth 'bw' = 0.08499
x y
Min. :-0.63983 Min. :0.002752
1st Qu.:-0.34213 1st Qu.:0.183526
Median :-0.04442 Median :0.405679
Mean :-0.04442 Mean :0.837928
3rd Qu.: 0.25328 3rd Qu.:1.611593
Max. : 0.55099 Max. :2.325300 As you can see, the bandwidth is calculated and provided in the output above. We then use the rkde function in place of the rnorm function to randomly sample from the kernel density estimate of our distribution. The input to the rkde function is fhat = kde(gspc_r, h = ...). Notice we have the returns in the gspc_r object and the bandwidth number in the h = option. From there, we can specify how many random observations we draw from the distribution. We then plot a histogram of this distribution to get an idea of the kernel density estimate distribution.
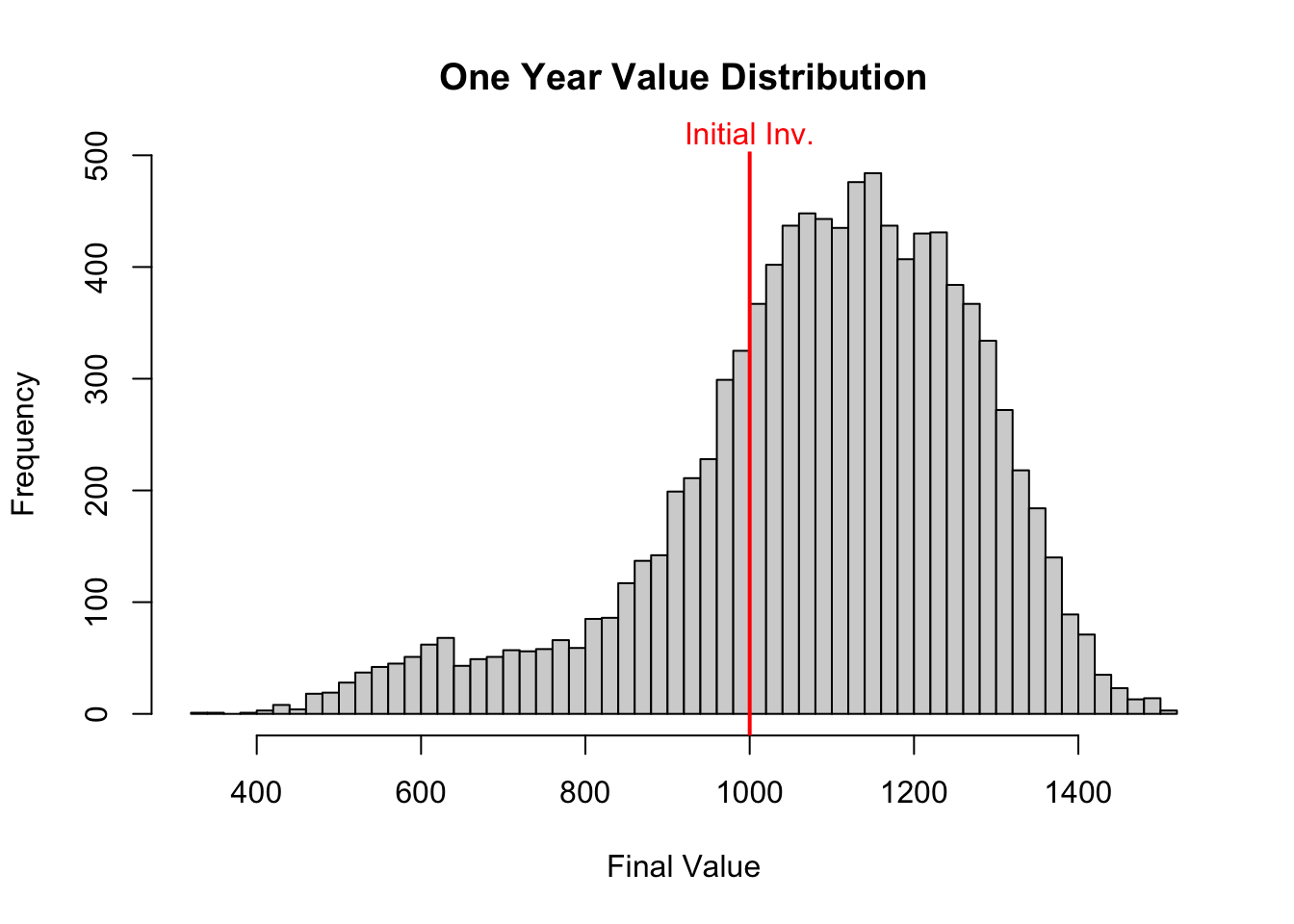
We can replace the normal distribution returns with these new KDE returns in our portfolio calculation to find the value after one year. This is done below with the new histogram of those returns.

This looks a little different than when we simulated with the normal distribution. The average is about the same, but there is a much larger tail on the left hand side which raises the chances of a loss.
Kernel density estimation can only happen when you have data to estimate a distribution on. First, we need to collect historical data on the S&P500 Index. We can do this through the yfinance package in Python. By putting in the stock ticker as it appears in the New York Stock Exchange, we can pull data from Yahoo Finance through this function. The ticker for the S&P500 Index is ^GSPC. The download function then gets us historical, daily opening prices, closing prices, high prices, and low prices. We will grab data all the way back to 2007. We want to calculate the annual return on the closing prices for the S&P500 Index. We can use the resample and pct_change functions in Python on the GSPC.Close column of the GSPC object to convert our data to annual ('YE') and then calculate the percentage chance.
[*********************100%***********************] 1 of 1 completedWe then plot a histogram of the data using the seaborn package and the histplot function.

Next we need to use the gaussian_kde function in the scipy.stats package in Python to estimate the kernel density estimation. We then use the resample function to randomly sample from the kernel density estimate of our distribution. From there, we can loop through how many random observations we draw from the distribution.
We can replace the normal distribution returns with these new KDE returns in our portfolio calculation to find the value after one year. This is done above with the new histogram of those returns calculated below.

This looks a little different than when we simulated with the normal distribution. The average is about the same, but there is a much larger tail on the left hand side which raises the chances of a loss.
Kernel density estimation can only happen when you have data to estimate a distribution on. First, we need to collect historical data on the S&P500 Index. We can do this through the getSymbols function in R. By putting in the stock ticker as it appears in the New York Stock Exchange, we can pull data from Yahoo Finance through this function. We will use this data gathered from R (see the R section of code for how) here in SAS for the analysis.
Next we need to use the PROC KDE procedure in SAS to estimate the bandwidth for the kernel density estimation. We use the GSPC dataset we gathered from R. The UNIVAR statement on the returns variable along with the UNISTATS option shows us some summary metrics on this estimated density along with the bandwidth.
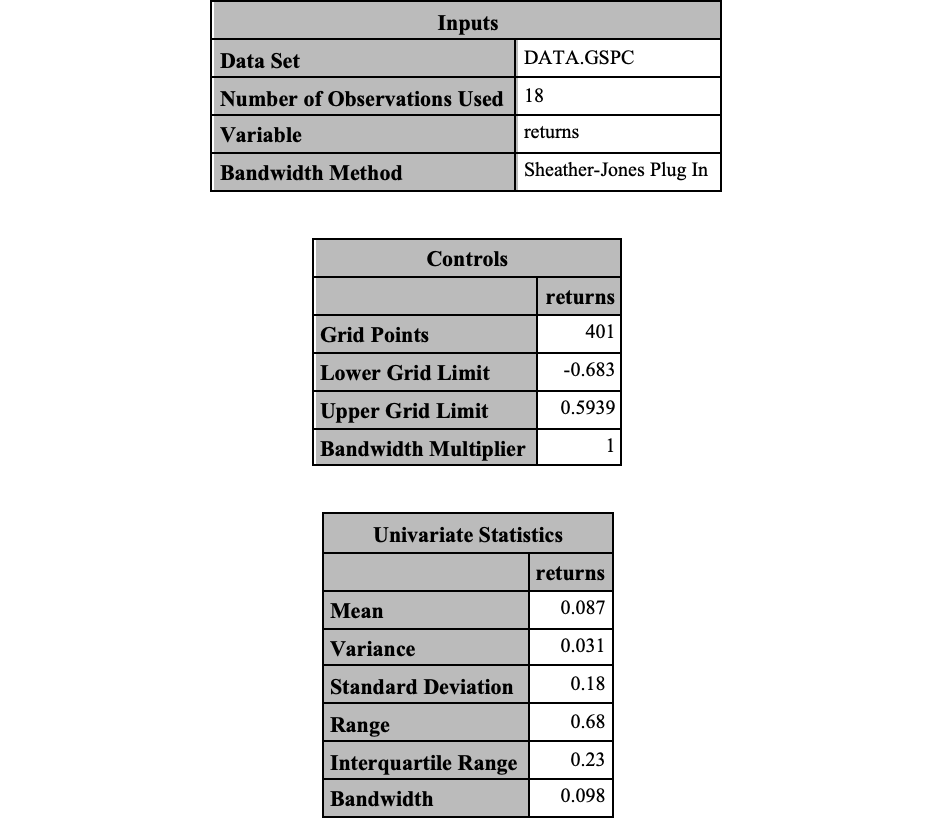

As you can see, the bandwidth is calculated and provided in the output above. We need to use PROC IML in SAS to random from this kernel density estimated distribution. IML stands for interactive matrix language and serves as a matrix language inside of SAS similar in vain to that of R. IML code is much different than SAS and won’t be covered in too much detail here. Essentially, the code below creates a function SmoothBootstrap that samples an observation from the imputed dataset. It then randomly generates a sample of 1 from a normal distribution around this point a certain number of prespecified times (here 10,000 in the code). We then import the data set using the USE and READ functions to take the variable returns and store it as x. From there we call the SmoothBootstrap function we created to sample from the kernel density estimate using the bandwidth from the output above as one of the inputs to this function. We add 1 to this vector of numbers and multiply by 1,000 to get the final portfolio value after one year. We then use CREATE to create a new dataset called Smooth to store the results with the APPEND statement. Once we are complete, we view the distribution with PROC SGPLOT as we didn’t previously when we used the normal distribution.
proc iml;
start SmoothBootstrap(x, B, Bandwidth);
N = 1;
s = Sample(x, N // B);
eps = j(B, N);
call randgen(eps, "Normal", 0, Bandwidth);
return( s + eps );
finish;
use SimRisk.GSPC;
read all var {returns} into x;
close SimRisk.GSPC;
call randseed(12345);
y = (1 + SmoothBootstrap(x, 10000, 0.098))*1000;
Est_y = y`;
create Smooth var {"Est_y"};
append;
close Smooth;
quit;
proc sgplot data=Smooth;
title 'One Year Value Distribution';
histogram Est_y;
refline 1000 / axis=x label='Initial Inv.' lineattrs=(color=red thickness=2);
keylegend / location=inside position=topright;
run;
This looks a little different than when we simulated with the normal distribution. The average is about the same, but there is a much larger tail on the left hand side which raises the chances of a loss.
The final choice for a distribution is the hypothesized future distribution. Maybe you know of an upcoming change that will occur in your variable so that the past information is not going to be the future distribution. For example, the volatility in the market is forecasted to increase, so instead of a standard deviation of 18% you forecast it to be 21%. In these situations, you can select any distribution of choice.
Complication arises in simulation when you are now simulating multiple inputs changing at the same time. Even when the distributions of these inputs are the same, the final result can still be hard to mathematically calculate. This shows the value of simulation since we don’t have to work out the mathematical equations for the combination of many input distributions.
When dealing with multiple input probability distributions there are some general facts we can use.
When a constant is added to a random variable (the variable with the distribution) then the distribution is the same, only shifted by the constant.
The addition of many distributions that are the same is rarely the same shape of distribution.
The product of many distributions that are the same is rarely the same shape of distribution.
Let’s adapt our previous example of investing in mutual funds. Now you want to invest $1,000 in the US stock market for 30 years. You invest in a mutual fund that tries to produce the same return as the S&P500 Index. Again, using the simple scenario where compounding isn’t continuous, we have the following value of our portfolio over 30 years:
\[ P_{30} = P_0 \times (1 + r_{0,1}) \times (1 + r_{1,2}) \times \cdots \times (1 + r_{29,30}) \]
The returns are structured as annual returns between each year which are now multiplied together. Again, we will assume annual returns follow a Normal distribution with historical mean of 9.75% and standard deviation of 18% for every year.
Let’s see how to do this in our software!
Simulation is rather easy to do in R because R is a vector language. This makes it so you don’t have to use as many loops as in other languages. However, in this example we use loops to give the reader a sense of how loops work in R. This example can be done without loops though. We start by setting a seed with the set.seed function so we can replicate our results. We then just use the rnorm function to randomly generate the possible values of the one year annual return. The n = option tells R the number of random draws you would like from the distribution. The mean = and sd = options define the mean and standard deviation of the normal distribution respectively. However, we do this within a couple of loops. The first loop is based on the number of simulations we want to run (here 10,000). We then calculate the return of 1 year and then loop through 29 more years of the same calculation by multiplying the additional return each iteration through the loop.
Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the summary function to calculate some summary statistics around our distribution of possible values of our portfolio after 30 years. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of P30, the values of our portfolio after 30 years.
Min. 1st Qu. Median Mean 3rd Qu. Max.
226.1 5858.1 11145.6 16542.4 20654.0 398106.5 
Not surprisingly, we can see that almost all of the values are above our initial investment of $1,000. In fact, on average, we would expect to make 9.75% return annually as that is the mean of our normal distribution. However, there is a spread to our returns and our returns are no longer normally distributed. They are now right skewed because we multiplied the effects year over year.
Simulation is rather easy to do in Python because Python is a vector language. This makes it so you don’t have to use as many loops as in other languages. However, in this example we use loops to give the reader a sense of how loops work in Python. This example can be done without loops though. We start by setting a seed with the random.seed function from numpy so we can replicate our results. We then just use the random.normal function to randomly generate the possible values of the one year annual return. The loc = and scale = options define the mean and standard deviation of the normal distribution respectively. However, we do this within a couple of loops. The first loop is based on the number of simulations we want to run (here 10,000). We then calculate the return of 1 year and then loop through 29 more years of the same calculation by multiplying the additional return each iteration through the loop.
import pandas as pd
import numpy as np
np.random.seed(112358)
data = []
for i in range(10000):
ret = np.random.normal(loc = 0.0975, scale = 0.18)
P0 = 1000
Pt = P0 * (1 + ret)
for j in range(29):
ret = np.random.normal(loc = 0.0975, scale = 0.18)
P0 = 1000
Pt = Pt * (1 + ret)
data.append(Pt)
df = pd.DataFrame(data)Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the describe function to calculate some summary statistics around our distribution of possible values of our portfolio after 30 years. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of P30, the values of our portfolio after 30 years.
0
count 10000.000000
mean 16451.359192
std 18070.162070
min 279.916011
25% 5808.839373
50% 10892.760778
75% 20105.048183
max 366697.241491
Not surprisingly, we can see that almost all of the values are above our initial investment of $1,000. In fact, on average, we would expect to make 9.75% return annually as that is the mean of our normal distribution. However, there is a spread to our returns and our returns are no longer normally distributed. They are now right skewed because we multiplied the effects year over year.
Simulations in SAS highly depend on the DATA step. This is easily seen in this example. We start by creating a new data set called SPIndex using the DATA step. We then use a do loop. Here we want to loop across the values of i from 1 to 10,000. We set up our initial investment value as P0 and define r as the return. We use the RAND function to draw a random value for our returns. This random value comes from the options specified in the RAND function. Here we specify that we want a 'Normal' distribution with a mean of 0.0975 and standard deviation of 0.18. We then calculate the portfolio value after 1 year and call it Pt. We then loop through 29 more years of the same calculation by multiplying the additional return each iteration through the loop. The OUTPUT statement saves this calculation and moves to the next step in the loop. The END statement defines the end of the loop.
Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the PROC MEANS procedure to calculate some summary statistics around our distribution of possible values of our portfolio after 30 years. We use the DATA = option to define the dataset of interest and the VAR statement to define the variable we are interested in summarizing, here Pt. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of Pt, the values of our portfolio after 30 years, using PROC SGPLOT and the HISTOGRAM statement for Pt.


Not surprisingly, we can see that almost all of the values are above our initial investment of $1,000. In fact, on average, we would expect to make 9.75% return annually as that is the mean of our normal distribution. However, there is a spread to our returns and our returns are no longer normally distributed. They are now right skewed because we multiplied the effects year over year.
Not all inputs may be independent of each other. Having correlations between your input variables adds even more complication to the simulation and final distribution. In these scenarios, we may need to simulate random variables that have correlation with each other.
One way to “add” correlation to data is to multiply the correlation into the data through matrix multiplication (linear algebra). Think about the approach we would take to change the variance of a single variable. If we had a variable X with a normal distribution (mean of 3 and variance of 2), then how could we get the variance to be 4 instead? We can do this in a few simple steps:
Standardize X to have a mean of 0 and variance of 1, \(Z = \frac{X-3}{\sqrt{2}}\)
Multiply Z by the standard deviation you desire, \(\sqrt{4} \times Z\)
Recenter Z back to its original mean, \(\sqrt{4} \times Z + 3\)
Now we have this new \(Y\) where \(Y = \sqrt{4} \times Z + 3\) which has the distribution that we want.
Now we have a variable that is normally distributed with a mean of 3 and variance of 4 like we wanted. We want to do the same thing on a multivariate scale to add correlation into data. We have a desired correlation matrix (that is a standardized version of the covariance matrix). We need to multiply this into the variables of interest to create our new variables. We do this in similar steps:
Standardize each column of our data (X)
Multiply this standardized X by the “square root” of the correlation matrix you want (this is called the Cholesky decomposition)
Convert this standardized X with the new correlation back to its original pre-standardized mean and variance.
The Cholesky decomposition is essentially the equivalent to the square root of a number. A square root of a number is whatever number when multiplied by itself gets the original number. The Cholesky decomposition is the same in matrix form. It is the matrix \(L\) when multiplied by itself \(L \times L^T\) , gives you the original matrix.
To add in the correlation to a set of data, we multiply this Cholesky decomposition of the desired covariance matrix by our data. If we had two variables, essentially this multiplication will leave the first column of data alone and “bend” the second column to look more like the first. This method works best for normally distributed variables, but still OK if the variables are symmetric and unimodal.
Let’s extend our 30 year investment example from above. Instead of just investing in stocks, you are splitting your money equally across stocks and bonds for 30 years. The individual calculations will be similar to above, just with a different set of returns for bonds as compared to stocks.
\[ P_{30,S} = P_{0,S} \times (1 + r_{0,1,S}) \times (1 + r_{1,2,S}) \times \cdots \times (1 + r_{29,30,S}) \]
\[ P_{30,B} = P_{0,B} \times (1 + r_{0,1,B}) \times (1 + r_{1,2,B}) \times \cdots \times (1 + r_{29,30,B}) \]
\[ P_{30} = P_{30,S} + P_{30,B} \]
Historically, Treasury bonds are perceived as safer investments so when the stock market does poorly more people invest in bonds. This leads to a negative correlation between the two. Let’s assume that our returns for stocks follow a normal distribution with mean of 9.75% and standard deviation of 18%, our bond returns follow a normal distribution with mean of 4% and standard deviation of 7%, and there is a correlation of -0.2 between the returns in any given year.
Let’s see how to solve this in our software!
Before running the simulation we need to set some things up. We first create a vector as long as the simulation we want to run full of 0’s. We will replace these 0’s, with the portfolio values as we go through the simulation. Next we create the correlation matrix we desire in the object R. In the next line, we take the Cholesky decomposition of R with the chol function. We then transpose this with the t function. From there we define some simple parameters around what percentage of investment we put into each stocks and bonds as well as the initial investment value itself.
We then create two functions. The first, called standardize takes a vector of data and creates a standardized version of that data. The second function, called destandardize, reverses this operation. By providing a vector of standardized data as well as the original version of the data, this function will transform the data back to its original mean and variance.
Next, we have the simulation itself. In this simulation, we loop through the same calculation many times. First, we simulate 30 returns for each stocks and bonds from their respective normal distributions. Next, we combine these vectors into a matrix after standardizing each of them. We when multiply the Cholesky decomposition by this standardized data matrix. From there, we use the destandardize function to put our data back to its original mean and variance. Now we have 30 years of correlated returns. From there we just loop through these returns to calculate the portfolio value over 30 years. Lastly, we sum up the returns from each of the two investments.
set.seed(112358)
for(j in 1:10000){
S.r <- rnorm(n=30, mean=0.0975, sd=0.18)
B.r <- rnorm(n=30, mean=0.04, sd=0.07)
Both.r <- cbind(standardize(S.r), standardize(B.r))
SB.r <- U %*% t(Both.r)
SB.r <- t(SB.r)
final.SB.r <- cbind(destandardize(SB.r[,1], S.r), destandardize(SB.r[,2], B.r))
Pt.B <- Initial*Perc.B
Pt.S <- Initial*Perc.S
for(i in 1:30){
Pt.B <- Pt.B*(1 + final.SB.r[i,2])
Pt.S <- Pt.S*(1 + final.SB.r[i,1])
}
Value.r.bal[j] <- Pt.B + Pt.S
}
hist(Value.r.bal, breaks=50, main='30 Year Value Distribution', xlab='Final Value')
abline(v = 1000, col="red", lwd=2)
mtext("Initial Inv.", at=1000, col="red")
By looking at the histogram above, we see what we would expect. We have a right skewed distribution with almost all possibilities resulting in a higher portfolio value after 30 years. This portfolio doesn’t have as high of a tail as only stocks due to the “safer” investment of the bonds.
invite you to play around with the balance of money allocated to stocks and bonds as the trade-off might surprise you with finding a good portfolio in terms of return and risk! For more on risk management, please see the code notes pack on risk management.
Before running the simulation we need to set some things up. We first create an empty list called data. We will replace these empty values with the portfolio values as we go through the simulation. Next we create the correlation matrix we desire in the object R. In the next line, we take the Cholesky decomposition of R with the linalg.cholesy function from scipy. From there we define some simple parameters around what percentage of investment we put into each stocks and bonds as well as the initial investment value itself.
We then create two functions. The first, called standardize takes a vector of data and creates a standardized version of that data. The second function, called destandardize, reverses this operation. By providing a vector of standardized data as well as the original version of the data, this function will transform the data back to its original mean and variance.
import scipy as sp
data = []
R = np.array([[1, -0.2], [-0.2, 1]])
U = sp.linalg.cholesky(R, lower = False)
Perc_B = 0.5
Perc_S = 0.5
Initial = 1000
def standardize(x):
x_std = (x - np.mean(x))/np.std(x)
return(x_std)
def destandardize(x_std, x):
x_old = (x_std * np.std(x)) + np.mean(x)
return(x_old)
Next, we have the simulation itself. In this simulation, we loop through the same calculation many times. First, we simulate 30 returns for each stocks and bonds from there respective normal distributions. Next, we combine these vectors into a numpy array after standardizing each of them. We when multiply the Cholesky decomposition by this standardized data array with matrix multiplication and the @ function. From there, we use the destandardize function to put our data back to its original mean and variance. Now we have 30 years of correlated returns. From there we just loop through these returns to calculate the portfolio value over 30 years. Lastly, we sum up the returns from each of the two investments.
np.random.seed(112358)
data = []
for i in range(10000):
S_ret = np.random.normal(loc = 0.0975, scale = 0.18, size = 30)
B_ret = np.random.normal(loc = 0.04, scale = 0.07, size = 30)
Both_ret = np.array([standardize(S_ret), standardize(B_ret)])
SB_ret = U @ Both_ret
final_SB_ret = np.array([destandardize(SB_ret[0], S_ret), destandardize(SB_ret[1], B_ret)])
Pt_B = Initial*Perc_B
Pt_S = Initial*Perc_S
for j in range(30):
Pt_S = Pt_S * (1 + final_SB_ret[0][j].item())
Pt_B = Pt_B * (1 + final_SB_ret[1][j].item())
Value = Pt_S + Pt_B
data.append(Value)
df = pd.DataFrame(data) 0
count 10000.000000
mean 9600.121387
std 8706.185183
min 1006.094513
25% 4434.048045
50% 7006.344637
75% 11515.744564
max 160826.255382
By looking at the histogram above, we see what we would expect. We have a right skewed distribution with almost all possibilities resulting in a higher portfolio value after 30 years. This portfolio doesn’t have as high of a tail as only stocks due to the “safer” investment of the bonds.
I invite you to play around with the balance of money allocated to stocks and bonds as the trade-off might surprise you with finding a good portfolio in terms of return and risk! For more on risk management, please see the code notes pack on risk management.
Pulling this off in SAS is much more difficult. First, we have to set up the problem. In the first data step, we create the correlation matrix, but we have to create it as many times as we have simulations. We create this in the Corr_Matrix dataset. Next, we create a Naive dataset that has values of 0 for both stocks and bonds as many times as we have simulations. Think of these as a starting point that we will eventually delete.
Next we use PROC MODEL to sample the random variables and build in the correlation structure. For each piece we initial set the value of either the stocks or bonds at their respective means. Then we simulate random normal distributions around these means. The Normal option here only has one input, the variance, since it will simulate around the mean we previously defined. Next we use the solve option to add in the correlation structure for each iteration in our simulation. From there we have a data option to store the generated data from the simulations by each iteration i. Lastly, we use a DATA step on our created data to delete that initial place holder row for each simulation.
data Corr_Matrix;
do i=1 to 10000;
_type_ = "corr";
_name_ = "S_r";
S_r = 1.0;
B_r = -0.2;
output;
_name_ = "B_r";
S_r = -0.2;
B_r = 1.0;
output;
end;
run;
data Naive;
do i=1 to 10000;
S_r=0;
B_r=0;
output;
end;
run;
proc model noprint;
/*Distributiuon of S*/
S_r = 0.0975;/*Mean of S*/
errormodel S_r ~Normal(0.0324); /*Variance is defined here as 0.18^2*/
/*Distribution of B*/
B_r = 0.04;/*Mean of B*/
errormodel B_r ~Normal(0.0049); /*Variance is defined here as 0.07^2*/
/*Generate the data and store them in the dataset work.Correlated_X */
solve S_r B_r/ random=30 sdata=Corr_Matrix
data=Naive out=Correlated_X(keep=S_r B_r i _rep_);
by i;
run;
quit;
data Correlated_X;
set Correlated_X;
by i;
if first.i then delete;
rename i=simulation;
rename _rep_=obs;
run;Now that we have our simulated, correlated returns, we need to calculate the portfolio value over the 30 years. Again, this isn’t as straight forward in SAS datasets since we typically manipulate columns, not rows. First, we will use PROC TRANSPOSE to create columns for each of the 30 years of returns and let the rows be each simulation. To do this we transpose the variables with the VAR statement and use the BY statement to keep the simulations as rows. In the next DATA step we just perform the portfolio calculation of multiplying the returns across columns. Finally, we transpose the data back with PROC TRANSPOSE and then plot to see our final distribution with PROC SGPLOT.
proc transpose data=Correlated_X out=SB30;
var S_r B_r;
by simulation;
run;
data SB30A;
set SB30;
P30 = 500*(1+COL1)*(1+COL2)*(1+COL3)*(1+COL4)*(1+COL5)*
(1+COL6)*(1+COL7)*(1+COL8)*(1+COL9)*(1+COL10)*
(1+COL11)*(1+COL12)*(1+COL13)*(1+COL14)*(1+COL15)*
(1+COL16)*(1+COL17)*(1+COL18)*(1+COL19)*(1+COL20)*
(1+COL21)*(1+COL22)*(1+COL23)*(1+COL24)*(1+COL25)*
(1+COL26)*(1+COL27)*(1+COL28)*(1+COL29)*(1+COL30);
run;
proc transpose data=SB30A out=SB30A_Final;
var P30;
by simulation;
run;
data SB30A_Final;
set SB30A_Final;
Value = S_r + B_r;
run;
proc sgplot data=SB30A_Final;
title '30 Year Value Distribution';
histogram Value;
refline 1000 / axis=x label='Initial Inv.' lineattrs=(color=red thickness=2);
keylegend / location=inside position=topright;
run;
By looking at the histogram above, we see what we would expect. We have a right skewed distribution with almost all possibilities resulting in a higher portfolio value after 30 years. This portfolio doesn’t have as high of a tail as only stocks due to the “safer” investment of the bonds.
I invite you to play around with the balance of money allocated to stocks and bonds as the trade-off might surprise you with finding a good portfolio in terms of return and risk! For more on risk management, please see the code notes pack on risk management.
The possible number of outcomes from a simulation is basically infinite. Essentially, simulations sample these values. Therefore, the accuracy of the estimates of these simulations depends on the number of simulated values. This leads to the question of how many simulations should we run.
Confidence interval theory in statistics helps reveal the relationship between the accuracy and number of simulations. For example, if we wanted to know the mean value from our simulation, we know the margin of error around the mean.
\[ MoE(\hat{x}) = t \times \frac{s}{\sqrt{n}} \]
In the above equation, \(n\) is the number of simulations that we are running, while \(s\) is the standard deviation of the estimated means from the simulations. Therefore, to double the accuracy, we need to approximately quadruple the number of simulations.
---
title: "Concepts Through Examples"
format:
html:
code-fold: show
code-tools: true
editor: visual
---
```{r}
#| include: false
library(reticulate)
use_condaenv("r-main")
```
# Introductory Example
The best way to learn simulation is through an example.
Suppose you want to invest \$1,000 (call this $P_0$) in the US stock market for one year. You invest in a mutual fund that tries to produce the same return as the S&P500 Index. Let's keep this example basic and only work with annual return. The price after one year can be calculated as follows:
$$
P_1 = P_0 \times (1 + r_{0,1})
$$
The term $r_{0,1}$ refers to the annual return from time point 0 to time point 1. Let's assume annual returns follow a Normal distribution with a historical mean of 9.75% and a standard deviation of 18%.
Let's see how we would simulate this problem in each of our software!
::: {.panel-tabset .nav-pills}
## R
Simulation is rather easy to do in R because R is a vector language. This makes it so you don't have to use as many loops as in other languages. This is easily seen in this example. We start by setting a seed with the `set.seed` function so we can replicate our results. We then just use the `rnorm` function to randomly generate the possible values of the one year annual return. The `n =` option tells R the number of random draws you would like from the distribution. The `mean =` and `sd =` options define the mean and standard deviation of the normal distribution respectively. This creates a vector of observations. With R's ability to do vector math, we can just add 1 to every element in the vector and multiply that by our initial investment value defined as the *P0* object below.
```{r}
set.seed(112358)
r <- rnorm(n=10000, mean=0.0975, sd=0.18)
P0 <- 1000
P1 <- P0*(1+r)
```
Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the `summary` function to calculate some summary statistics around our distribution of possible values of our portfolio after one year. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of *P1*, the values of our portfolio after one year.
```{r}
summary(P1)
```
```{r}
hist(P1, breaks=50, main='One Year Value Distribution', xlab='Final Value')
abline(v = 1000, col="red", lwd=2)
mtext("Initial Inv.", at=1000, col="red")
```
Not surprisingly, we can see that a majority of the values are above our initial investment of \$1,000. In fact, on average, we would expect to make 9.75% return as that is the mean of our normal distribution. However, there is a spread to our returns as well so not all returns are above our initial investment. We can see there are a portion of scenarios that have us fall below our initial investment value.
## Python
Simulation is rather easy to do in Python because Python is a vector language. In this example we are going to use loops to quickly simulate through our example. We start by setting a seed with the `random.seed` function from `numpy` so we can replicate our results. We then just use the `random.normal` function from `numpy` to randomly generate the possible values of the one year annual return. The `for` loop tells Python the number of random draws you would like from the distribution. The `loc =` and `scale =` options define the mean and standard deviation of the normal distribution respectively. This creates a vector of observations as we `append` the values on the end of each other as we loop through. As we go, we can just add 1 to every element in the vector and multiply that by our initial investment value defined as the *P0* object below.
```{python}
import pandas as pd
import numpy as np
np.random.seed(112358)
data = []
for i in range(10000):
ret = np.random.normal(loc = 0.0975, scale = 0.18)
P0 = 1000
P1 = P0 * (1 + ret)
data.append(P1)
df = pd.DataFrame(data)
```
Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the `describe` function to calculate some summary statistics around our distribution of possible values of our portfolio after one year. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of *P1*, the values of our portfolio after one year using the `histplot` from `seaborn`.
```{python}
df.describe()
```
```{python}
import seaborn as sns
ax = sns.histplot(data = df)
ax.set(xlabel = "Final Value")
ax.axvline(x = 1000, color = "red")
```
Not surprisingly, we can see that a majority of the values are above our initial investment of \$1,000. In fact, on average, we would expect to make 9.75% return as that is the mean of our normal distribution. However, there is a spread to our returns as well so not all returns are above our initial investment. We can see there are a portion of scenarios that have us fall below our initial investment value.
## SAS
Simulations in SAS highly depend on the `DATA` step. This is easily seen in this example. We start by creating a new data set called *SPIndex* using the `DATA` step. We then use a `do` loop. Here we want to loop across the values of *i* from 1 to 10,000. We set up our initial investment value as *P0* and define *r* as the return. We use the `RAND` function to draw a random value for our returns. This random value comes from the options specified in the `RAND` function. Here we specify that we want a `'Normal'` distribution with a mean of 0.0975 and standard deviation of 0.18. We then calculate the portfolio value after 1 year and call it *P1*. The `OUTPUT` statement saves this calculation and moves to the next step in the loop. The `END` statement defines the end of the loop.
```{r}
#| eval: false
data SPIndex;
do i = 1 to 10000;
P0 = 1000;
r = RAND('Normal', 0.0975, 0.18);
P1 = P0*(1 + r);
output;
end;
run;
```
{fig-align="center" width="7in" height="1.11in"}
Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the `PROC MEANS` procedure to calculate some summary statistics around our distribution of possible values of our portfolio after one year. We use the `DATA =` option to define the dataset of interest and the `VAR` statement to define the variable we are interested in summarizing, here *P1*. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of *P1*, the values of our portfolio after one year, using `PROC SGPLOT` and the `HISTOGRAM` statement for *P1*.
```{r}
#| eval: false
proc means data=SPIndex;
var P1;
run;
proc sgplot data=SPIndex;
title 'One Year Value Distribution';
histogram P1;
refline 1000 / axis=x label='Initial Inv.' lineattrs=(color=red thickness=2);
keylegend / location=inside position=topright;
run;
```
{fig-align="center" width="6in"}
Not surprisingly, we can see that a majority of the values are above our initial investment of \$1,000. In fact, on average, we would expect to make 9.75% return as that is the mean of our normal distribution. However, there is a spread to our returns as well so not all returns are above our initial investment. We can see there are a portion of scenarios that have us fall below our initial investment value.
:::
How did we select the normal distribution for our returns? Is that a good guess of a distribution? That we will need to find out in our next section.
# Distribution Selection
When designing your simulations, the biggest choice comes from the decision of the distribution on the inputs that vary. There are 3 common methods for selecting these distributions:
1. Common Probability Distribution
2. Historical (Empirical) Distribution
3. Hypothesized Future Distribution
## Common Probability Distribution
Typically, we assume a common probability distribution for inputs that vary in a simulation. We did this in our above example where we just assumed returns followed a normal distribution. When selecting distributions, we need to first decide if our variables are discrete or continuous in nature. A discrete variable take on outcomes that you can list out (even if you can not list all of them). Continuous variables on the other hand take on any possible value in a interval (even if the interval is unbounded).
::: {.panel-tabset .nav-pills}
## Discrete Distribution Examples
Some commonly used discrete distributions for simulations are the following:
- Uniform distribution
- Poisson distribution
In the discrete uniform, every discrete value of the distribution has an equal probability of occurring.
{fig-align="center" width="5in"}
The Poisson distribution is best used for when you are counting events. It is bounded below by 0 and takes on all non-negative integer values with differing probabilities of occurrences based on the location of the distribution.
{fig-align="center" width="5in"}
## Continuous Distribution Examples
Some commonly used continuous distributions for simulations are the following:
- Uniform distribution
- Triangle distribution
- Normal distribution
- Student's t-distribution
- Lognormal distribution
- Exponential distribution
- Beta distribution
Much like its discrete counterpart, in the continuous uniform distribution every value of the distribution has an equal probability of occurring.
{fig-align="center" width="5in"}
The triangle distribution is a great distribution for business scenarios where individuals might only be able to tell you three things - the worst case scenario, the best case scenario, and the most likely (in the middle) scenario. With these three points we can define the triangle distribution.
{fig-align="center" width="5in"}
The Gaussian (normal) distribution is one of the most popular distributions out there. Bell-shaped and symmetric with nice mathematical properties, the normal distribution is used for inputs in many simulations.
{fig-align="center" width="5in"}
The student's t-distribution is bell-shaped and symmetric like the normal distribution, but it has thicker tails. This allows for more variability than the normal distribution provides.
{fig-align="center" width="5in"}
The lognormal distribution is very popular in the financial simulation world as it has nice asymmetric properties which stock returns sometimes follow.
{fig-align="center" width="5in"}
The exponential distribution is great for simulating risky (sometimes called *tail*) events. It is one of many distributions like it used in Extreme Value Theory.
{fig-align="center" width="5in"}
The Beta distribution is a family of distributions that take many shapes. Some of the most popular shapes in terms of simulations are the "bathtub" like shape that has higher probabilities of edge cases happening as compared to the middle cases.
{fig-align="center" width="5in"}
:::
## Historical (Empirical) Distributions
If you are unsure of the distribution of the data you are trying to simulate, you can estimate it using the process of **kernel density estimation**. Kernel density estimation is a non-parametric method of estimating distributions of data through smoothing out of data values.
The kernel density estimator is as follows:
$$
\hat{f(x)} = \frac{1}{n\times h} \sum_{i=1}^n \kappa (\frac{x - x_i}{h})
$$
In the above equation $\kappa$ is the kernel function. The kernel function builds a distribution centered around each of the points in your dataset. Imagine a small normal distribution built around each point and then adding these normal distributions together to form one larger distribution. The default kernel function distribution in a lot of software is the normal distribution, but there are other options like the quadratic, triangle, and Epanechnikov. The In the above equation $h$ is the bandwidth. The bandwidth controls the variability around each point. The larger the variability, the more variation is built around each point through the distribution as seen in the chart below:
{fig-align="center" width="7in"}
The above plot shows kernel density estimates of data sampled from a standard normal distribution. The actual distribution is highlighted with the dashed line above. Three estimates with different bandwidths are shown. The smaller the bandwidth, the smaller the variability around each point, but also the more highly fit our curve is to our data. The larger the bandwidth, the more variability around each point which smooths out the curve much more. We want to find the balance. There is a lot of research that has been done and still ongoing on how to best select bandwidth. We will leave it up to the computer to optimize this decision for us.
Once we have this kernel density estimate for our data, we can sample from this estimated distribution for our simulation. In our previous example we assumed a normal distribution for our returns of our mutual fund. Now, let's build an empirical distribution through kernel density estimation and sample from that instead of the normal distribution.
Let's see how to do this in each of our software!
::: {.panel-tabset .nav-pills}
## R
Kernel density estimation can only happen when you have data to estimate a distribution on. First, we need to collect historical data on the S&P500 Index. We can do this through the `getSymbols` function in R. By putting in the stock ticker as it appears in the New York Stock Exchange, we can pull data from Yahoo Finance through this function. The ticker for the S&P500 Index is *\^GSPC*. The `getSymbols` function then gets us historical, daily opening prices, closing prices, high prices, and low prices all the way back to 2007. We want to calculate the annual return on the closing prices for the S&P500 Index. We can use the `periodReturn` function in R on the *GSPC.Close* column of the *GSPC* object created from the `getSymbols` function. The `period =` option defines the period you want to calculate returns on. We want yearly returns. We then plot a histogram of the data.
```{r}
#| warning: false
#| error: false
#| message: false
library(quantmod)
tickers <- "^GSPC"
getSymbols(tickers)
gspc_r <- periodReturn(GSPC$GSPC.Close, period = "yearly")
hist(gspc_r, main='Historical S&P500', xlab='S&P500 Annual Returns')
```
Next we need to use the `density` function in R to estimate the bandwidth for the kernel density estimation.
```{r}
#| warning: false
#| error: false
#| message: false
Density.GSPC <- density(gspc_r)
Density.GSPC
```
As you can see, the bandwidth is calculated and provided in the output above. We then use the `rkde` function in place of the `rnorm` function to randomly sample from the kernel density estimate of our distribution. The input to the `rkde` function is `fhat = kde(gspc_r, h = ...)`. Notice we have the returns in the *gspc_r* object and the bandwidth number in the `h =` option. From there, we can specify how many random observations we draw from the distribution. We then plot a histogram of this distribution to get an idea of the kernel density estimate distribution.
```{r}
library(ks)
set.seed(112358)
Est.GSPC <- rkde(fhat = kde(gspc_r, h = Density.GSPC$bw), n = 10000)
hist(Est.GSPC, breaks = 50, main = 'KDE of Historical S&P500', xlab = 'S&P500 Annual Returns')
```
We can replace the normal distribution returns with these new KDE returns in our portfolio calculation to find the value after one year. This is done below with the new histogram of those returns.
```{r}
r <- Est.GSPC
P0 <- 1000
P1 <- P0*(1+r)
hist(P1, breaks=50, main='One Year Value Distribution', xlab='Final Value')
abline(v = 1000, col="red", lwd=2)
mtext("Initial Inv.", at=1000, col="red")
```
This looks a little different than when we simulated with the normal distribution. The average is about the same, but there is a much larger tail on the left hand side which raises the chances of a loss.
## Python
Kernel density estimation can only happen when you have data to estimate a distribution on. First, we need to collect historical data on the S&P500 Index. We can do this through the `yfinance` package in Python. By putting in the stock ticker as it appears in the New York Stock Exchange, we can pull data from Yahoo Finance through this function. The ticker for the S&P500 Index is *\^GSPC*. The `download` function then gets us historical, daily opening prices, closing prices, high prices, and low prices. We will grab data all the way back to 2007. We want to calculate the annual return on the closing prices for the S&P500 Index. We can use the `resample` and `pct_change` functions in Python on the *GSPC.Close* column of the *GSPC* object to convert our data to annual (`'YE'`) and then calculate the percentage chance.
```{r}
#| echo: false
gspc_df <- data.frame(gspc_r)
```
```{python}
import yfinance as yf
GSPC = yf.download("^GSPC", start = "2007-01-01")
gspc_r = GSPC['Close'].resample('YE').ffill().pct_change()
gspc_r = gspc_r.drop(gspc_r.index[0])
```
We then plot a histogram of the data using the `seaborn` package and the `histplot` function.
```{python}
import seaborn as sns
ax = sns.histplot(data = gspc_r)
ax.set(xlabel = "S&P500 Annual Returns")
```
Next we need to use the `gaussian_kde` function in the `scipy.stats` package in Python to estimate the kernel density estimation. We then use the `resample` function to randomly sample from the kernel density estimate of our distribution. From there, we can loop through how many random observations we draw from the distribution.
```{python}
from scipy.stats import gaussian_kde
kernel = gaussian_kde(gspc_r['^GSPC'])
data = []
for i in range(10000):
ret = kernel.resample(size = 1).item()
P0 = 1000
P1 = P0 * (1 + ret)
data.append(P1)
df = pd.DataFrame(data)
```
We can replace the normal distribution returns with these new KDE returns in our portfolio calculation to find the value after one year. This is done above with the new histogram of those returns calculated below.
```{python}
import seaborn as sns
ax = sns.histplot(data = df)
ax.set(xlabel = "Final Value")
ax.axvline(x = 1000, color = "red")
```
This looks a little different than when we simulated with the normal distribution. The average is about the same, but there is a much larger tail on the left hand side which raises the chances of a loss.
## SAS
Kernel density estimation can only happen when you have data to estimate a distribution on. First, we need to collect historical data on the S&P500 Index. We can do this through the `getSymbols` function in R. By putting in the stock ticker as it appears in the New York Stock Exchange, we can pull data from Yahoo Finance through this function. We will use this data gathered from R (see the R section of code for how) here in SAS for the analysis.
Next we need to use the `PROC KDE` procedure in SAS to estimate the bandwidth for the kernel density estimation. We use the *GSPC* dataset we gathered from R. The `UNIVAR` statement on the *returns* variable along with the `UNISTATS` option shows us some summary metrics on this estimated density along with the bandwidth.
```{r}
#| eval: false
proc kde data=SimRisk.GSPC;
univar returns / unistats;
run;
```
{fig-align="center" width="7in"}
{fig-align="center" width="6in"}
As you can see, the bandwidth is calculated and provided in the output above. We need to use `PROC IML` in SAS to random from this kernel density estimated distribution. IML stands for interactive matrix language and serves as a matrix language inside of SAS similar in vain to that of R. IML code is much different than SAS and won't be covered in too much detail here. Essentially, the code below creates a function `SmoothBootstrap` that samples an observation from the imputed dataset. It then randomly generates a sample of 1 from a normal distribution around this point a certain number of prespecified times (here 10,000 in the code). We then import the data set using the `USE` and `READ` functions to take the variable *returns* and store it as *x*. From there we call the `SmoothBootstrap` function we created to sample from the kernel density estimate using the bandwidth from the output above as one of the inputs to this function. We add 1 to this vector of numbers and multiply by 1,000 to get the final portfolio value after one year. We then use `CREATE` to create a new dataset called *Smooth* to store the results with the `APPEND` statement. Once we are complete, we view the distribution with `PROC SGPLOT` as we didn't previously when we used the normal distribution.
```{r}
#| eval: false
proc iml;
start SmoothBootstrap(x, B, Bandwidth);
N = 1;
s = Sample(x, N // B);
eps = j(B, N);
call randgen(eps, "Normal", 0, Bandwidth);
return( s + eps );
finish;
use SimRisk.GSPC;
read all var {returns} into x;
close SimRisk.GSPC;
call randseed(12345);
y = (1 + SmoothBootstrap(x, 10000, 0.098))*1000;
Est_y = y`;
create Smooth var {"Est_y"};
append;
close Smooth;
quit;
proc sgplot data=Smooth;
title 'One Year Value Distribution';
histogram Est_y;
refline 1000 / axis=x label='Initial Inv.' lineattrs=(color=red thickness=2);
keylegend / location=inside position=topright;
run;
```
{fig-align="center" width="6in"}
This looks a little different than when we simulated with the normal distribution. The average is about the same, but there is a much larger tail on the left hand side which raises the chances of a loss.
:::
## Hypothesized Future Distribution
The final choice for a distribution is the hypothesized future distribution. Maybe you know of an upcoming change that will occur in your variable so that the past information is not going to be the future distribution. For example, the volatility in the market is forecasted to increase, so instead of a standard deviation of 18% you forecast it to be 21%. In these situations, you can select any distribution of choice.
# Compounding and Correlations
Complication arises in simulation when you are now simulating multiple inputs changing at the same time. Even when the distributions of these inputs are the same, the final result can still be hard to mathematically calculate. This shows the value of simulation since we don't have to work out the mathematical equations for the combination of many input distributions.
When dealing with multiple input probability distributions there are some general facts we can use.
1. When a constant is added to a **random variable** (the variable with the distribution) then the distribution is the same, only shifted by the constant.
2. The addition of many distributions that are the same is rarely the same shape of distribution.
- The exception to this are INDEPENDENT normal distributions.
3. The product of many distributions that are the same is rarely the same shape of distribution.
- The exception to this are INDEPENDENT lognormal distributions.
## Extended Example
Let's adapt our previous example of investing in mutual funds. Now you want to invest \$1,000 in the US stock market for 30 years. You invest in a mutual fund that tries to produce the same return as the S&P500 Index. Again, using the simple scenario where compounding isn't continuous, we have the following value of our portfolio over 30 years:
$$
P_{30} = P_0 \times (1 + r_{0,1}) \times (1 + r_{1,2}) \times \cdots \times (1 + r_{29,30})
$$
The returns are structured as annual returns between each year which are now multiplied together. Again, we will assume annual returns follow a Normal distribution with historical mean of 9.75% and standard deviation of 18% for **every** year.
Let's see how to do this in our software!
::: {.panel-tabset .nav-pills}
## R
Simulation is rather easy to do in R because R is a vector language. This makes it so you don't have to use as many loops as in other languages. However, in this example we use loops to give the reader a sense of how loops work in R. This example can be done without loops though. We start by setting a seed with the `set.seed` function so we can replicate our results. We then just use the `rnorm` function to randomly generate the possible values of the one year annual return. The `n =` option tells R the number of random draws you would like from the distribution. The `mean =` and `sd =` options define the mean and standard deviation of the normal distribution respectively. However, we do this within a couple of loops. The first loop is based on the number of simulations we want to run (here 10,000). We then calculate the return of 1 year and then loop through 29 more years of the same calculation by multiplying the additional return each iteration through the loop.
```{r}
set.seed(112358)
P30 <- rep(0,10000)
for(i in 1:10000){
P0 <- 1000
r <- rnorm(n=1, mean=0.0975, sd=0.18)
Pt <- P0*(1 + r)
for(j in 1:29){
r <- rnorm(n=1, mean=0.0975, sd=0.18)
Pt <- Pt*(1+r)
}
P30[i] <- Pt
}
```
Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the `summary` function to calculate some summary statistics around our distribution of possible values of our portfolio after 30 years. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of *P30*, the values of our portfolio after 30 years.
```{r}
summary(P30)
hist(P30, breaks=50, main='30 Year Value Distribution', xlab='Final Value')
abline(v = 1000, col="red", lwd=2)
mtext("Initial Inv.", at=1000, col="red")
```
Not surprisingly, we can see that almost all of the values are above our initial investment of \$1,000. In fact, on average, we would expect to make 9.75% return annually as that is the mean of our normal distribution. However, there is a spread to our returns and our returns are no longer normally distributed. They are now right skewed because we multiplied the effects year over year.
## Python
Simulation is rather easy to do in Python because Python is a vector language. This makes it so you don't have to use as many loops as in other languages. However, in this example we use loops to give the reader a sense of how loops work in Python. This example can be done without loops though. We start by setting a seed with the `random.seed` function from `numpy` so we can replicate our results. We then just use the `random.normal` function to randomly generate the possible values of the one year annual return. The `loc =` and `scale =` options define the mean and standard deviation of the normal distribution respectively. However, we do this within a couple of loops. The first loop is based on the number of simulations we want to run (here 10,000). We then calculate the return of 1 year and then loop through 29 more years of the same calculation by multiplying the additional return each iteration through the loop.
```{python}
import pandas as pd
import numpy as np
np.random.seed(112358)
data = []
for i in range(10000):
ret = np.random.normal(loc = 0.0975, scale = 0.18)
P0 = 1000
Pt = P0 * (1 + ret)
for j in range(29):
ret = np.random.normal(loc = 0.0975, scale = 0.18)
P0 = 1000
Pt = Pt * (1 + ret)
data.append(Pt)
df = pd.DataFrame(data)
```
Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the `describe` function to calculate some summary statistics around our distribution of possible values of our portfolio after 30 years. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of *P30*, the values of our portfolio after 30 years.
```{python}
df.describe()
import seaborn as sns
ax = sns.histplot(data = df)
ax.set(xlabel = "Final Value")
ax.axvline(x = 1000, color = "red")
```
Not surprisingly, we can see that almost all of the values are above our initial investment of \$1,000. In fact, on average, we would expect to make 9.75% return annually as that is the mean of our normal distribution. However, there is a spread to our returns and our returns are no longer normally distributed. They are now right skewed because we multiplied the effects year over year.
## SAS
Simulations in SAS highly depend on the `DATA` step. This is easily seen in this example. We start by creating a new data set called *SPIndex* using the `DATA` step. We then use a `do` loop. Here we want to loop across the values of *i* from 1 to 10,000. We set up our initial investment value as *P0* and define *r* as the return. We use the `RAND` function to draw a random value for our returns. This random value comes from the options specified in the `RAND` function. Here we specify that we want a `'Normal'` distribution with a mean of 0.0975 and standard deviation of 0.18. We then calculate the portfolio value after 1 year and call it *Pt*. We then loop through 29 more years of the same calculation by multiplying the additional return each iteration through the loop. The `OUTPUT` statement saves this calculation and moves to the next step in the loop. The `END` statement defines the end of the loop.
```{r}
#| eval: false
data SPIndex30;
do i = 1 to 10000;
P0 = 1000;
r = RAND('Normal', 0.0975, 0.18);
Pt = P0*(1 + r);
do j = 1 to 29;
r = RAND('Normal', 0.0975, 0.18);
Pt = Pt*(1 + r);
end;
output;
end;
run;
```
Then our simulation is complete! Next, we just need to view the distribution of our simulation. Below we use the `PROC MEANS` procedure to calculate some summary statistics around our distribution of possible values of our portfolio after 30 years. We use the `DATA =` option to define the dataset of interest and the `VAR` statement to define the variable we are interested in summarizing, here *Pt*. The best way to truly look at results of a simulation though are through plots. We then plot the histogram of *Pt*, the values of our portfolio after 30 years, using `PROC SGPLOT` and the `HISTOGRAM` statement for *Pt*.
```{r}
#| eval: false
proc means data=SPIndex30;
var Pt;
run;
proc sgplot data=SPIndex30;
title 'One Year Value Distribution';
histogram Pt;
refline 1000 / axis=x label='Initial Inv.' lineattrs=(color=red thickness=2);
keylegend / location=inside position=topright;
run;
```
{fig-align="center" width="7in" height="1.03in"}
{fig-align="center" width="7in"}
Not surprisingly, we can see that almost all of the values are above our initial investment of \$1,000. In fact, on average, we would expect to make 9.75% return annually as that is the mean of our normal distribution. However, there is a spread to our returns and our returns are no longer normally distributed. They are now right skewed because we multiplied the effects year over year.
:::
## Adding Correlation
Not all inputs may be independent of each other. Having correlations between your input variables adds even more complication to the simulation and final distribution. In these scenarios, we may need to simulate random variables that have correlation with each other.
One way to "add" correlation to data is to multiply the correlation into the data through matrix multiplication (linear algebra). Think about the approach we would take to change the variance of a single variable. If we had a variable X with a normal distribution (mean of 3 and variance of 2), then how could we get the variance to be 4 instead? We can do this in a few simple steps:
1. Standardize X to have a mean of 0 and variance of 1, $Z = \frac{X-3}{\sqrt{2}}$
2. Multiply Z by the standard deviation you desire, $\sqrt{4} \times Z$
3. Recenter Z back to its original mean, $\sqrt{4} \times Z + 3$
Now we have this new $Y$ where $Y = \sqrt{4} \times Z + 3$ which has the distribution that we want.
Now we have a variable that is normally distributed with a mean of 3 and variance of 4 like we wanted. We want to do the same thing on a multivariate scale to add correlation into data. We have a desired correlation matrix (that is a standardized version of the covariance matrix). We need to multiply this into the variables of interest to create our new variables. We do this in similar steps:
1. Standardize each column of our data (X)
2. Multiply this standardized X by the "square root" of the correlation matrix you want (this is called the Cholesky decomposition)
3. Convert this standardized X with the new correlation back to its original pre-standardized mean and variance.
The Cholesky decomposition is essentially the equivalent to the square root of a number. A square root of a number is whatever number when multiplied by itself gets the original number. The Cholesky decomposition is the same in matrix form. It is the matrix $L$ when multiplied by itself $L \times L^T$ , gives you the original matrix.
To add in the correlation to a set of data, we multiply this Cholesky decomposition of the desired covariance matrix by our data. If we had two variables, essentially this multiplication will leave the first column of data alone and "bend" the second column to look more like the first. This method works best for normally distributed variables, but still OK if the variables are symmetric and unimodal.
Let's extend our 30 year investment example from above. Instead of just investing in stocks, you are splitting your money equally across stocks and bonds for 30 years. The individual calculations will be similar to above, just with a different set of returns for bonds as compared to stocks.
$$
P_{30,S} = P_{0,S} \times (1 + r_{0,1,S}) \times (1 + r_{1,2,S}) \times \cdots \times (1 + r_{29,30,S})
$$
$$
P_{30,B} = P_{0,B} \times (1 + r_{0,1,B}) \times (1 + r_{1,2,B}) \times \cdots \times (1 + r_{29,30,B})
$$
$$
P_{30} = P_{30,S} + P_{30,B}
$$
Historically, Treasury bonds are perceived as safer investments so when the stock market does poorly more people invest in bonds. This leads to a negative correlation between the two. Let's assume that our returns for stocks follow a normal distribution with mean of 9.75% and standard deviation of 18%, our bond returns follow a normal distribution with mean of 4% and standard deviation of 7%, and there is a correlation of -0.2 between the returns in any given year.
Let's see how to solve this in our software!
::: {.panel-tabset .nav-pills}
## R
Before running the simulation we need to set some things up. We first create a vector as long as the simulation we want to run full of 0's. We will replace these 0's, with the portfolio values as we go through the simulation. Next we create the correlation matrix we desire in the object *R*. In the next line, we take the Cholesky decomposition of *R* with the `chol` function. We then transpose this with the `t` function. From there we define some simple parameters around what percentage of investment we put into each stocks and bonds as well as the initial investment value itself.
We then create two functions. The first, called `standardize` takes a vector of data and creates a standardized version of that data. The second function, called `destandardize`, reverses this operation. By providing a vector of standardized data as well as the original version of the data, this function will transform the data back to its original mean and variance.
```{r}
Value.r.bal <- rep(0,10000)
R <- matrix(data=cbind(1,-0.2, -0.2, 1), nrow=2)
U <- t(chol(R))
Perc.B <- 0.5
Perc.S <- 0.5
Initial <- 1000
standardize <- function(x){
x.std = (x - mean(x))/sd(x)
return(x.std)
}
destandardize <- function(x.std, x){
x.old = (x.std * sd(x)) + mean(x)
return(x.old)
}
```
Next, we have the simulation itself. In this simulation, we loop through the same calculation many times. First, we simulate 30 returns for each stocks and bonds from their respective normal distributions. Next, we combine these vectors into a matrix after standardizing each of them. We when multiply the Cholesky decomposition by this standardized data matrix. From there, we use the `destandardize` function to put our data back to its original mean and variance. Now we have 30 years of correlated returns. From there we just loop through these returns to calculate the portfolio value over 30 years. Lastly, we sum up the returns from each of the two investments.
```{r}
set.seed(112358)
for(j in 1:10000){
S.r <- rnorm(n=30, mean=0.0975, sd=0.18)
B.r <- rnorm(n=30, mean=0.04, sd=0.07)
Both.r <- cbind(standardize(S.r), standardize(B.r))
SB.r <- U %*% t(Both.r)
SB.r <- t(SB.r)
final.SB.r <- cbind(destandardize(SB.r[,1], S.r), destandardize(SB.r[,2], B.r))
Pt.B <- Initial*Perc.B
Pt.S <- Initial*Perc.S
for(i in 1:30){
Pt.B <- Pt.B*(1 + final.SB.r[i,2])
Pt.S <- Pt.S*(1 + final.SB.r[i,1])
}
Value.r.bal[j] <- Pt.B + Pt.S
}
hist(Value.r.bal, breaks=50, main='30 Year Value Distribution', xlab='Final Value')
abline(v = 1000, col="red", lwd=2)
mtext("Initial Inv.", at=1000, col="red")
```
By looking at the histogram above, we see what we would expect. We have a right skewed distribution with almost all possibilities resulting in a higher portfolio value after 30 years. This portfolio doesn't have as high of a tail as only stocks due to the "safer" investment of the bonds.
invite you to play around with the balance of money allocated to stocks and bonds as the trade-off might surprise you with finding a good portfolio in terms of return and risk! For more on risk management, please see the code notes pack on [risk management](https://ariclabarr.com/risk-management/).
## Python
Before running the simulation we need to set some things up. We first create an empty list called `data`. We will replace these empty values with the portfolio values as we go through the simulation. Next we create the correlation matrix we desire in the object *R*. In the next line, we take the Cholesky decomposition of *R* with the `linalg.cholesy` function from `scipy`. From there we define some simple parameters around what percentage of investment we put into each stocks and bonds as well as the initial investment value itself.
We then create two functions. The first, called `standardize` takes a vector of data and creates a standardized version of that data. The second function, called `destandardize`, reverses this operation. By providing a vector of standardized data as well as the original version of the data, this function will transform the data back to its original mean and variance.
```{python}
import scipy as sp
data = []
R = np.array([[1, -0.2], [-0.2, 1]])
U = sp.linalg.cholesky(R, lower = False)
Perc_B = 0.5
Perc_S = 0.5
Initial = 1000
def standardize(x):
x_std = (x - np.mean(x))/np.std(x)
return(x_std)
def destandardize(x_std, x):
x_old = (x_std * np.std(x)) + np.mean(x)
return(x_old)
```
Next, we have the simulation itself. In this simulation, we loop through the same calculation many times. First, we simulate 30 returns for each stocks and bonds from there respective normal distributions. Next, we combine these vectors into a `numpy` `array` after standardizing each of them. We when multiply the Cholesky decomposition by this standardized data array with matrix multiplication and the `@` function. From there, we use the `destandardize` function to put our data back to its original mean and variance. Now we have 30 years of correlated returns. From there we just loop through these returns to calculate the portfolio value over 30 years. Lastly, we sum up the returns from each of the two investments.
```{python}
np.random.seed(112358)
data = []
for i in range(10000):
S_ret = np.random.normal(loc = 0.0975, scale = 0.18, size = 30)
B_ret = np.random.normal(loc = 0.04, scale = 0.07, size = 30)
Both_ret = np.array([standardize(S_ret), standardize(B_ret)])
SB_ret = U @ Both_ret
final_SB_ret = np.array([destandardize(SB_ret[0], S_ret), destandardize(SB_ret[1], B_ret)])
Pt_B = Initial*Perc_B
Pt_S = Initial*Perc_S
for j in range(30):
Pt_S = Pt_S * (1 + final_SB_ret[0][j].item())
Pt_B = Pt_B * (1 + final_SB_ret[1][j].item())
Value = Pt_S + Pt_B
data.append(Value)
df = pd.DataFrame(data)
```
```{python}
df.describe()
import seaborn as sns
ax = sns.histplot(data = df)
ax.set(xlabel = "Final Value")
ax.axvline(x = 1000, color = "red")
```
By looking at the histogram above, we see what we would expect. We have a right skewed distribution with almost all possibilities resulting in a higher portfolio value after 30 years. This portfolio doesn't have as high of a tail as only stocks due to the "safer" investment of the bonds.
I invite you to play around with the balance of money allocated to stocks and bonds as the trade-off might surprise you with finding a good portfolio in terms of return and risk! For more on risk management, please see the code notes pack on [risk management](https://ariclabarr.com/risk-management/).
## SAS
Pulling this off in SAS is much more difficult. First, we have to set up the problem. In the first data step, we create the correlation matrix, but we have to create it as many times as we have simulations. We create this in the *Corr_Matrix* dataset. Next, we create a *Naive* dataset that has values of 0 for both stocks and bonds as many times as we have simulations. Think of these as a starting point that we will eventually delete.
Next we use `PROC MODEL` to sample the random variables and build in the correlation structure. For each piece we initial set the value of either the stocks or bonds at their respective means. Then we simulate random normal distributions around these means. The `Normal` option here only has one input, the variance, since it will simulate around the mean we previously defined. Next we use the `solve` option to add in the correlation structure for each iteration in our simulation. From there we have a `data` option to store the generated data from the simulations by each iteration *i*. Lastly, we use a `DATA` step on our created data to delete that initial place holder row for each simulation.
```{r}
#| eval: false
data Corr_Matrix;
do i=1 to 10000;
_type_ = "corr";
_name_ = "S_r";
S_r = 1.0;
B_r = -0.2;
output;
_name_ = "B_r";
S_r = -0.2;
B_r = 1.0;
output;
end;
run;
data Naive;
do i=1 to 10000;
S_r=0;
B_r=0;
output;
end;
run;
proc model noprint;
/*Distributiuon of S*/
S_r = 0.0975;/*Mean of S*/
errormodel S_r ~Normal(0.0324); /*Variance is defined here as 0.18^2*/
/*Distribution of B*/
B_r = 0.04;/*Mean of B*/
errormodel B_r ~Normal(0.0049); /*Variance is defined here as 0.07^2*/
/*Generate the data and store them in the dataset work.Correlated_X */
solve S_r B_r/ random=30 sdata=Corr_Matrix
data=Naive out=Correlated_X(keep=S_r B_r i _rep_);
by i;
run;
quit;
data Correlated_X;
set Correlated_X;
by i;
if first.i then delete;
rename i=simulation;
rename _rep_=obs;
run;
```
Now that we have our simulated, correlated returns, we need to calculate the portfolio value over the 30 years. Again, this isn't as straight forward in SAS datasets since we typically manipulate columns, not rows. First, we will use `PROC TRANSPOSE` to create columns for each of the 30 years of returns and let the rows be each simulation. To do this we transpose the variables with the `VAR` statement and use the `BY` statement to keep the simulations as rows. In the next `DATA` step we just perform the portfolio calculation of multiplying the returns across columns. Finally, we transpose the data back with `PROC TRANSPOSE` and then plot to see our final distribution with `PROC SGPLOT`.
```{r}
#| eval: false
proc transpose data=Correlated_X out=SB30;
var S_r B_r;
by simulation;
run;
data SB30A;
set SB30;
P30 = 500*(1+COL1)*(1+COL2)*(1+COL3)*(1+COL4)*(1+COL5)*
(1+COL6)*(1+COL7)*(1+COL8)*(1+COL9)*(1+COL10)*
(1+COL11)*(1+COL12)*(1+COL13)*(1+COL14)*(1+COL15)*
(1+COL16)*(1+COL17)*(1+COL18)*(1+COL19)*(1+COL20)*
(1+COL21)*(1+COL22)*(1+COL23)*(1+COL24)*(1+COL25)*
(1+COL26)*(1+COL27)*(1+COL28)*(1+COL29)*(1+COL30);
run;
proc transpose data=SB30A out=SB30A_Final;
var P30;
by simulation;
run;
data SB30A_Final;
set SB30A_Final;
Value = S_r + B_r;
run;
proc sgplot data=SB30A_Final;
title '30 Year Value Distribution';
histogram Value;
refline 1000 / axis=x label='Initial Inv.' lineattrs=(color=red thickness=2);
keylegend / location=inside position=topright;
run;
```
{fig-align="center" width="7in"}
By looking at the histogram above, we see what we would expect. We have a right skewed distribution with almost all possibilities resulting in a higher portfolio value after 30 years. This portfolio doesn't have as high of a tail as only stocks due to the "safer" investment of the bonds.
I invite you to play around with the balance of money allocated to stocks and bonds as the trade-off might surprise you with finding a good portfolio in terms of return and risk! For more on risk management, please see the code notes pack on [risk management](https://ariclabarr.com/risk-management/).
:::
# How Many and How Long
The possible number of outcomes from a simulation is basically infinite. Essentially, simulations sample these values. Therefore, the accuracy of the estimates of these simulations depends on the number of simulated values. This leads to the question of how many simulations should we run.
Confidence interval theory in statistics helps reveal the relationship between the accuracy and number of simulations. For example, if we wanted to know the mean value from our simulation, we know the margin of error around the mean.
$$
MoE(\hat{x}) = t \times \frac{s}{\sqrt{n}}
$$
In the above equation, $n$ is the number of simulations that we are running, while $s$ is the standard deviation of the estimated means from the simulations. Therefore, to double the accuracy, we need to approximately quadruple the number of simulations.