Code
library(AmesHousing)
ames <- make_ordinal_ames()First, we need to first explore our data before building any models to try and explain/predict our categorical target variable. With categorical variables, we can look at the distribution of the categories as well as see if this distribution has any association with other variables. For this analysis we are going to the popular Ames housing dataset. This dataset contains information on home values for a sample of nearly 3,000 houses in Ames, Iowa in the early 2000s. To access this data, we first add the AmesHousing package and create the nicely formatted data with the make_ordinal_ames() function.
Imagine you worked for a real estate agency and got a bonus check if you sold a house above $175,000 in value. Let’s create this variable in our data:
Before exploring any relationships between predictor variables and the target variable Bonus, we need to split our dataset into training and testing pieces. Because models are prone to discovering small, spurious patterns on the data that is used to create them (the training data), we set aside the validation and/or testing data to get a clear view of how they might perform on new data that the models have never seen before.
You are interested in what variables might be associated with obtaining a higher chance of getting a bonus (selling a house above $175,000). An association exists between two categorical variables if the distribution of one variable changes when the value of the other categorical variable changes. If there is no association, the distribution of the first variable is the same regardless of the value of the other variable. For example, if we wanted to know if obtaining a bonus on selling a house in Ames, Iowa was associated with whether the house had central air we could look at the distribution of bonus eligible houses. If we observe that 42% of homes with central air are bonus eligible and 42% of homes without central air are bonus eligible, then it appears that central air has no bearing on whether the home is bonus eligible. However, if instead we observe that only 3% of homes without central air are bonus eligible, but 44% of home with central air are bonus eligible, then it appears that having central air might be related to a home being bonus eligible.
To understand the distribution of categorical variables we need to look at frequency tables. A frequency table shows the number of observations that occur in certain categories or intervals. A one-way frequency table examines all the categories of one variable. These are easily visualized with bar charts.
Let’s see how to do this in each of our softwares!
Let’s look at the distribution of both bonus eligibility and central air using the table function. The ggplot function with the geom_bar function allows us to view our data in a bar chart.
N Y
147 1904 
Frequency tables show single variables, but if we want to explore two variables together we look at cross-tabulation tables. A cross-tabulation table shows the number of observations for each combination of the row and column variables.
Let’s again examine bonus eligibility, but this time across levels of central air. Again, we can use the table function. The prop.table function allows us to compare two variables in terms of proportions instead of frequencies.
0 1
N 142 5
Y 1069 835
0 1
N 0.069234520 0.002437835
Y 0.521209166 0.407118479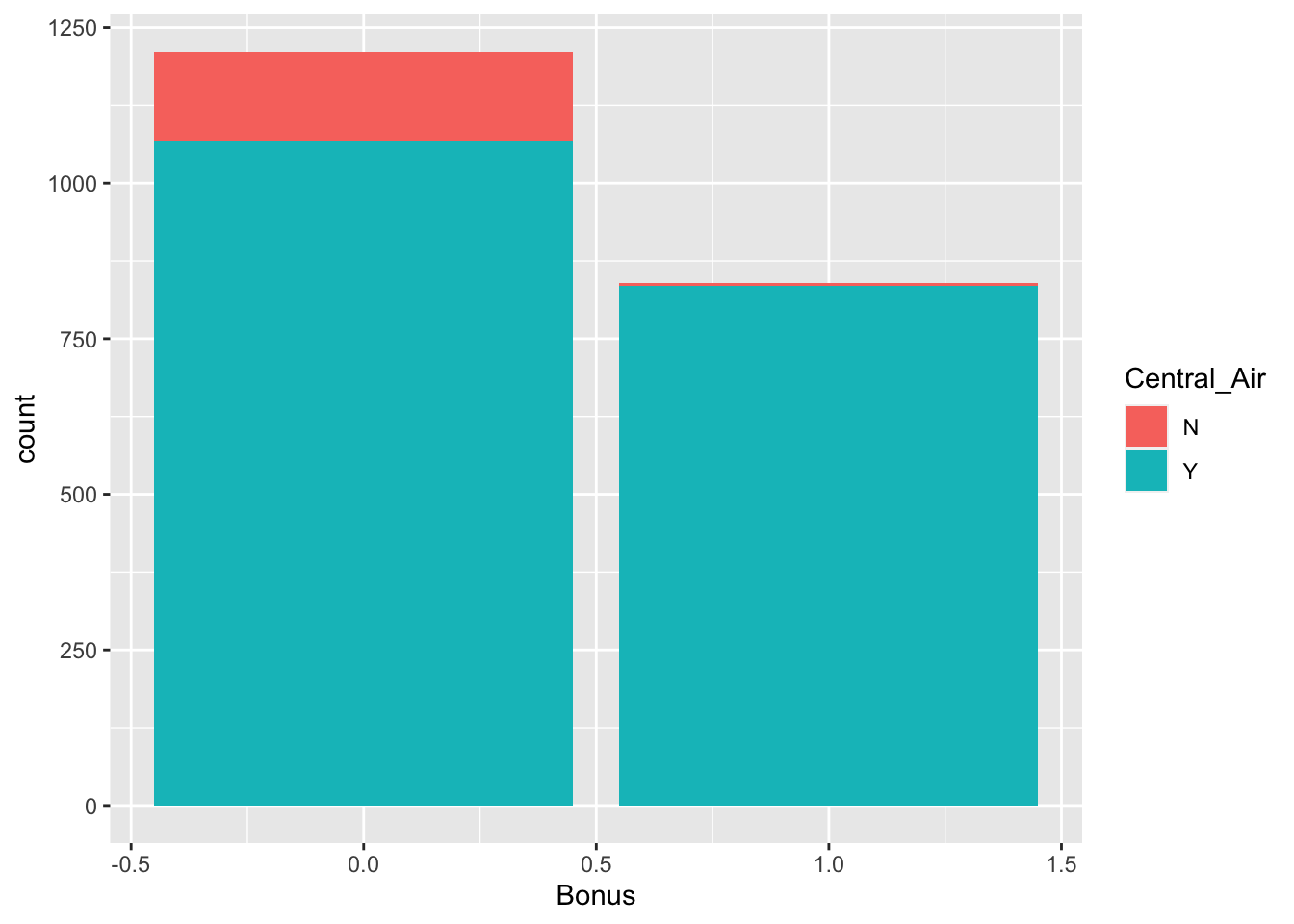
From the above output we can see that 147 homes have no central air with only 5 of them being bonus eligible. However, there are 1904 homes that have central air with 835 of them being bonus eligible. For an even more detailed breakdown we can use the CrossTable function.
Cell Contents
|-------------------------|
| N |
| Expected N |
| N / Row Total |
| N / Col Total |
| N / Table Total |
|-------------------------|
Total Observations in Table: 2051
| train$Bonus
train$Central_Air | 0 | 1 | Row Total |
------------------|-----------|-----------|-----------|
N | 142 | 5 | 147 |
| 86.795 | 60.205 | |
| 0.966 | 0.034 | 0.072 |
| 0.117 | 0.006 | |
| 0.069 | 0.002 | |
------------------|-----------|-----------|-----------|
Y | 1069 | 835 | 1904 |
| 1124.205 | 779.795 | |
| 0.561 | 0.439 | 0.928 |
| 0.883 | 0.994 | |
| 0.521 | 0.407 | |
------------------|-----------|-----------|-----------|
Column Total | 1211 | 840 | 2051 |
| 0.590 | 0.410 | |
------------------|-----------|-----------|-----------|
Statistics for All Table Factors
Pearson's Chi-squared test
------------------------------------------------------------
Chi^2 = 92.35121 d.f. = 1 p = 7.258146e-22
Pearson's Chi-squared test with Yates' continuity correction
------------------------------------------------------------
Chi^2 = 90.68591 d.f. = 1 p = 1.683884e-21
The advantage of the CrossTable function is that we can easily get not only the frequencies, but the cell, row, and column proportions. For example, the third number in each cell gives us the row proportion. For homes without central air, 96.6% of them are not bonus eligible, while 3.4% of them are. For homes with central air, 56.1% of the homes are not bonus eligible, while 43.9% of them are. This would appear that the distribution of bonus eligible homes changes across levels of central air - a relationship between the two variables. This expected relationship needs to be tested statistically for verification. The expected = TRUE option provides an expected cell count for each cell. These expected counts help calculate the tests of association in the next section.
To make sure we have the same train and test datasets in Python, we can use the following code to bring the datasets from R into Python (using R Studio). If we were to randomly sample the original data (even with setting a seed), R and Python would select different observations which makes it hard to compare results.
(2051, 83)(879, 83)Let’s look at the distribution of both bonus eligibility and central air using the value_counts attribute of the train dataset. The countplot function allows us to view our data in a bar chart.
Bonus
0.0 1211
1.0 840
Name: count, dtype: int64
Central_Air
Y 1904
N 147
Name: count, dtype: int64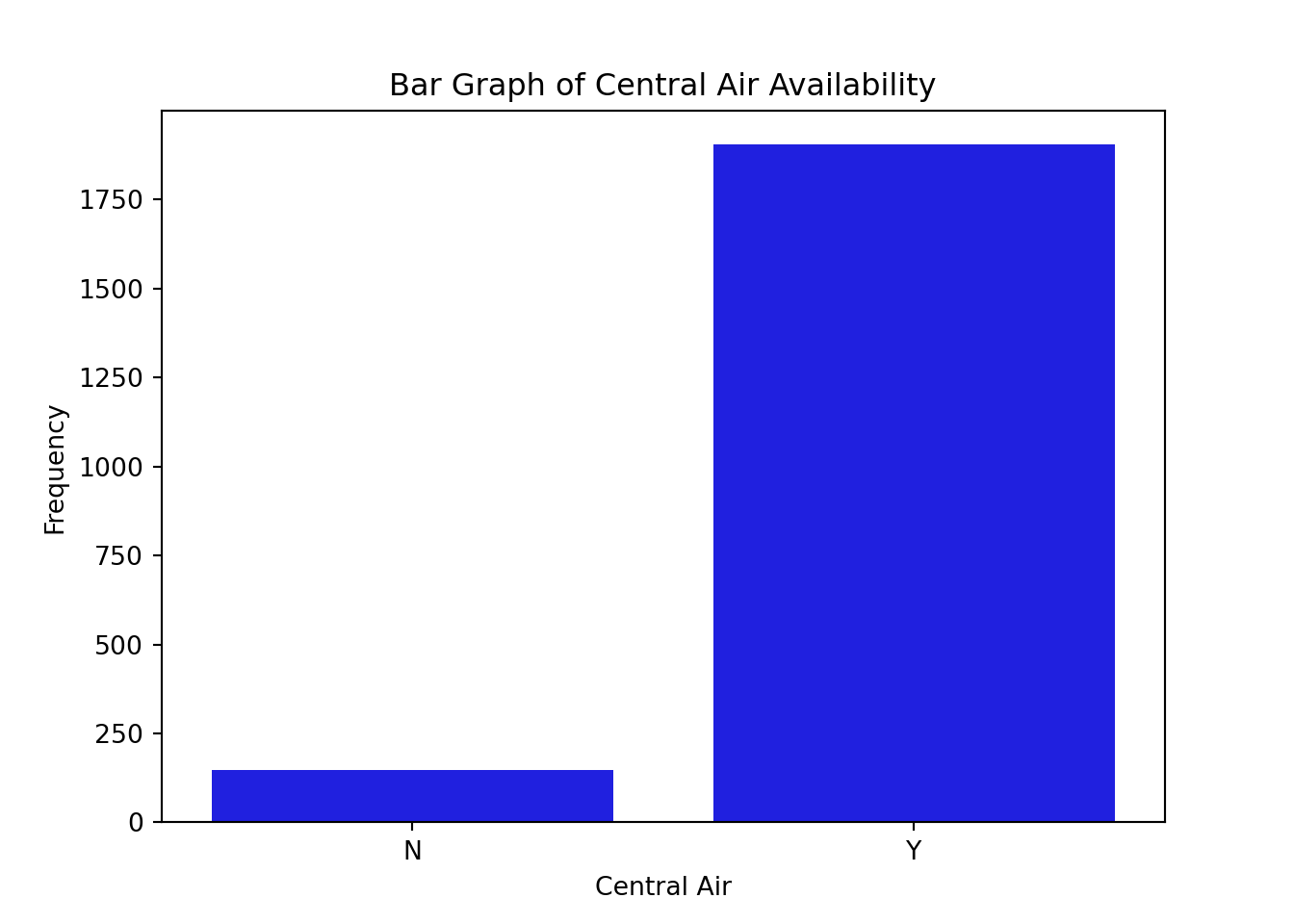
Frequency tables show single variables, but if we want to explore two variables together we look at cross-tabulation tables. A cross-tabulation table shows the number of observations for each combination of the row and column variables.
Let’s again examine bonus eligibility, but this time across levels of central air. Here, we can use the crosstab function from pandas.
Bonus 0.0 1.0
Central_Air
N 142 5
Y 1069 835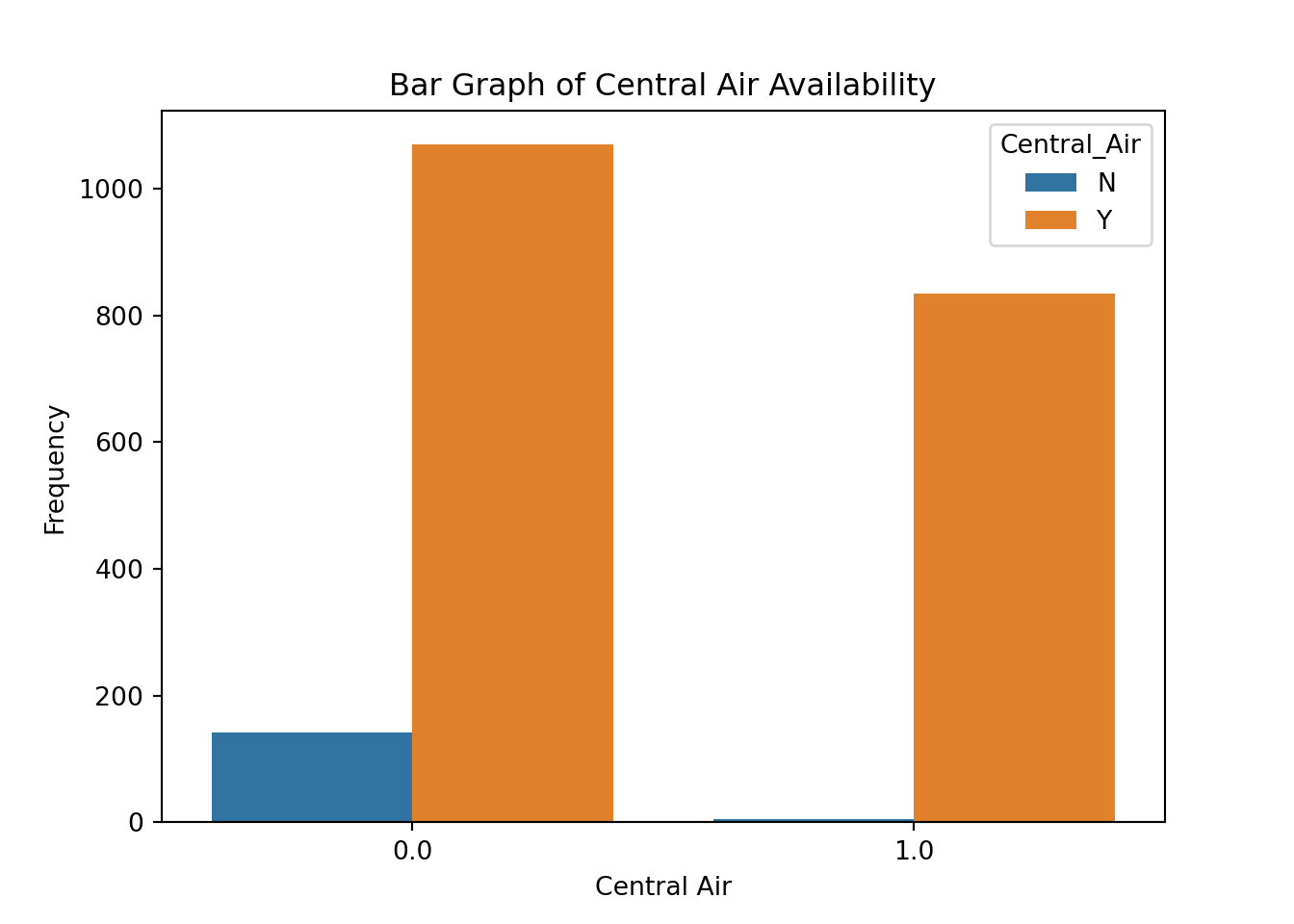
From the above output we can see that 147 homes have no central air with only 5 of them being bonus eligible. However, there are 1904 homes that have central air with 835 of them being bonus eligible.
Let’s look at the distribution of both bonus eligibility and central air using the FREQ procedure. The TABLES statement will build us frequency tables on any set of variables. Here we list the variables Bonus, Central_Air, and the cross-tabulation between Bonus and Central_Air using the * notation between them. Frequency tables show single variables, but if we want to explore two variables together we look at cross-tabulation tables. A cross-tabulation table shows the number of observations for each combination of the row and column variables. The plots option allows us to look at the frequency plot of each of these with the scale changed to percentages instead of the default of raw counts.
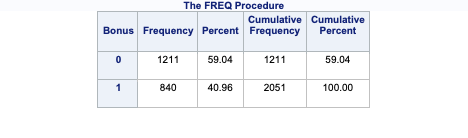
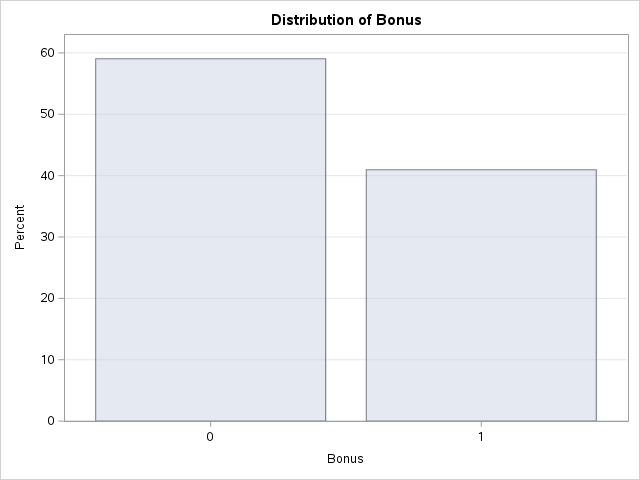
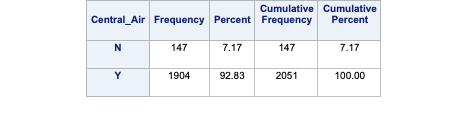
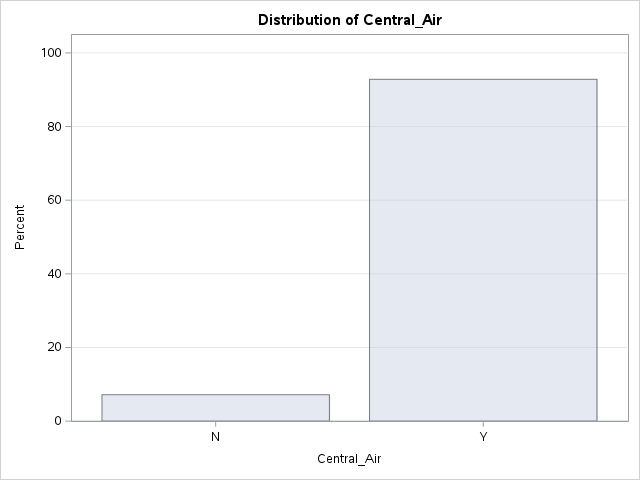
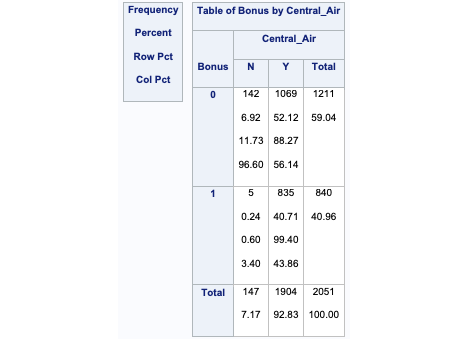
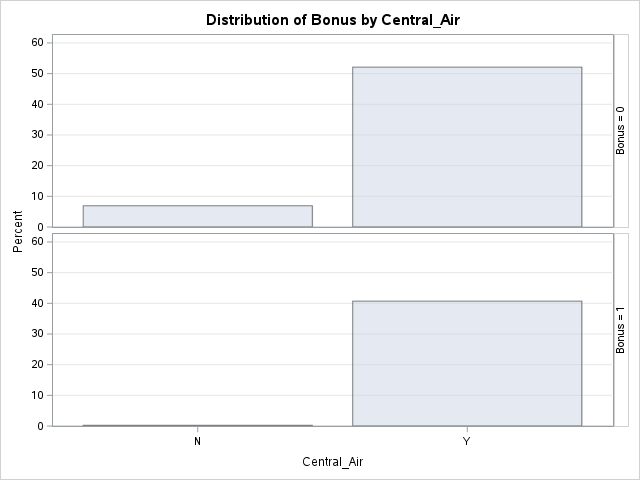
From the above output we can see that 147 homes have no central air with only 5 of them being bonus eligible. However, there are 1904 homes that have central air with 835 of them being bonus eligible.
The advantage of the FREQ procedure in SAS is that we can easily get not only the frequencies, but the cell, row, and column proportions. For example, the fourth number in each cell gives us the column proportion. For homes without central air, 96.6% of them are not bonus eligible, while 3.4% of them are. For homes with central air, 56.1% of the homes are not bonus eligible, while 43.9% of them are. This would appear that the distribution of bonus eligible homes changes across levels of central air - a relationship between the two variables. This expected relationship needs to be tested statistically for verification. We can also use the expected option in the TABLES statement to provide an expected cell count for each cell. These expected counts help calculate the tests of association in the next section.
We have statistical tests to evaluate relationships between two categorical variables. The null hypothesis for these statistical tests is that the two variables have no association - the distribution of one variable does not change across levels of another variable. The alternative hypothesis is an association between the two variables - the distribution of one variable changes across levels of another variable.
These statistical tests follow a \(\chi^2\)-distribution. The \(\chi^2\)-distribution is a distribution that has the following characteristics:
Bounded below by 0
Right skewed
One set of degrees of freedom
A plot of a variety of \(\chi^2\)-distributions is shown here:

Two common \(\chi^2\) tests are the Pearson and Likelihood Ratio \(\chi^2\) tests. They compare the observed count of observations in each cell of a cross-tabulation table to their expected count if there was no relationship. The expected cell count applies the overall distribution of one variable across all the levels of the other variable. For example, overall 59% of all homes are not bonus eligible. If that were to apply to every level of central air, then the 147 homes without central air would be expected to have 86.8 ( $ = 147 $ ) of them would be bonus eligible while 60.2 ( $ = 147 $ ) of them would not be bonus eligible. We actually observe 142 and 5 homes for each of these categories respectively. The further the observed data is from the expected data, the more evidence we have that there is a relationship between the two variables.
The test statistic for the Pearson \(\chi^2\) test is the following:
\[ \chi^2_P = \sum_{i=1}^R \sum_{j=1}^C \frac{(Obs_{i,j} - Exp_{i,j})^2}{Exp_{i,j}} \]
From the equation above, the closer that the observed count of each cross-tabulation table cell (across all rows and columns) to the expected count, the smaller the test statistic. As with all hypothesis tests, the smaller the test statistic, the larger the p-value, implying less evidence for the alternative hypothesis.
Another common test is the Likelihood Ratio test. The test statistic for this is the following:
\[ \chi^2_L = 2 \times \sum_{i=1}^R \sum_{j=1}^C Obs_{i,j} \times \log(\frac{Obs_{i,j}}{Exp_{i,j}}) \]
The p-value comes from a \(\chi^2\)-distribution with degrees of freedom that equal the product of the number of rows minus one and the number of columns minus one. Both of the above tests have a sample size requirement. The sample size requirement is 80% or more of the cells in the cross-tabulation table need expected counts larger than 5.
For smaller sample sizes, this might be hard to meet. In those situations, we can use a more computationally expensive test called Fisher’s exact test. This test calculates every possible permutation of the data being evaluated to calculate the p-value without any distributional assumptions.
Both the Pearson and Likelihood Ratio \(\chi^2\) tests can handle any type of categorical variable (either ordinal, nominal, or both). However, ordinal variables provide us extra information since the order of the categories actually matters compared to nominal categories. We can test for even more with ordinal variables against other ordinal variables whether two ordinal variables have a linear association as compared to just a general one. An ordinal test for association is the Mantel-Haenszel \(\chi^2\) test. The test statistic for the Mantel-Haenszel \(\chi^2\) test is the following:
\[ \chi^2_{MH} = (n-1)r^2 \] where \(r^2\) is the Pearson correlation between the column and row variables. This test follows a \(\chi^2\)-distribution with only one degree of freedom.
Let’s see how to do each of these tests in each of our softwares!
Let’s examine the relationship between central air and bonus eligibility with the Pearson and Likelihood Ratio tests using the assocstats function on our table object comparing Central_Air to Bonus.
Loading required package: grid X^2 df P(> X^2)
Likelihood Ratio 121.499 1 0
Pearson 92.351 1 0
Phi-Coefficient : 0.212
Contingency Coeff.: 0.208
Cramer's V : 0.212 The above results shows an extremely small p-value that is below any reasonable significance level. This implies that we have statistical evidence for a relationship between having central air and bonus eligibility of homes. The p-value comes from a \(\chi^2\)-distribution with degrees of freedom that equal the product of the number of rows minus one and the number of columns minus one.
Since both the central air and bonus eligibility variables are binary, they are ordinal. Since they are both ordinal, we should use the Mantel-Haenszel \(\chi^2\) test with the CMHtest function. In the main output table, the first row is the Mantel-Haenszel \(\chi^2\) test.
Loading required package: gnm
Attaching package: 'vcdExtra'The following object is masked from 'package:dplyr':
summarise Chisq Df Prob
9.230619e+01 1.000000e+00 7.425180e-22 From here we can see another extremely small p-value as we saw in the earlier, more general \(\chi^2\) tests.
Although not applicable in this dataset, if we had a small sample size we could use the Fisher’s exact test. To perform this test we can use the fisher.test function.
Fisher's Exact Test for Count Data
data: table(train$Central_Air, train$Bonus)
p-value < 2.2e-16
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
9.213525 69.646380
sample estimates:
odds ratio
22.16545 We see the same results as with the other tests because the assumptions were met for sample size.
Let’s examine the relationship between central air and bonus eligibility with the Pearson and Likelihood Ratio tests using the chi2_contingency function on our crosstab object comparing Central_Air to Bonus.
Chi2ContingencyResult(statistic=90.6859058522855, pvalue=1.6838843977848939e-21, dof=1, expected_freq=array([[ 86.79522184, 60.20477816],
[1124.20477816, 779.79522184]]))The above results shows an extremely small p-value that is below any reasonable significance level. This implies that we have statistical evidence for a relationship between having central air and bonus eligibility of homes. The p-value comes from a \(\chi^2\)-distribution with degrees of freedom that equal the product of the number of rows minus one and the number of columns minus one.
Since both the central air and bonus eligibility variables are binary, they are ordinal. Since they are both ordinal, we should use the Mantel-Haenszel \(\chi^2\) test. However, at the time of writing this, Python does not have a built in function for this.
Although not applicable in this dataset, if we had a small sample size we could use the Fisher’s exact test. To perform this test we can use the fisher_exact function.
SignificanceResult(statistic=22.18334892422825, pvalue=1.0365949500671678e-27)We see the same results as with the other tests because the assumptions were met for sample size.
Let’s examine the relationship between central air and bonus eligibility with the Pearson and Likelihood Ratio tests using the same FREQ procedure with some different options. The chisq option gives the results of the \(\chi^2\) tests. The expected, cellchi2, nocol, and nopercent options change the values provided in the cells. The expected values in each cell refer to the expected values in the calculations for the tests above. The cellchi2 gives the calculation of the Pearson test in each cell. The relrisk option also provides us with odds ratios which we discuss in the next section.
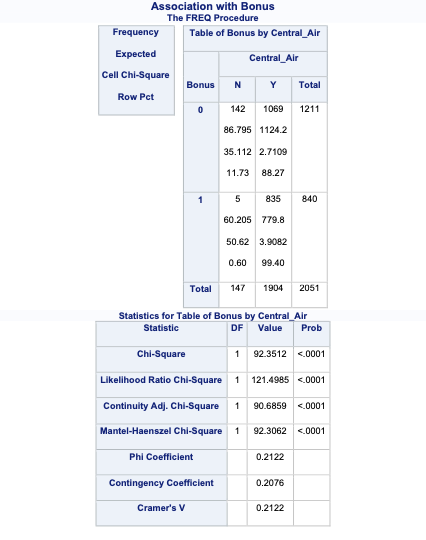

The above results shows an extremely small p-value that is below any reasonable significance level for either the Pearson (just labeled “Chi-Squared” above) or the Likelihood Ratio test. This implies that we have statistical evidence for a relationship between having central air and bonus eligibility of homes. The p-value comes from a \(\chi^2\)- distribution with degrees of freedom that equal the product of the number of rows minus one and the number of columns minus one.
Since both the central air and bonus eligibility variables are binary, they are ordinal. Since they are both ordinal, we should use the Mantel-Haenszel \(\chi^2\) test output. The beauty of SAS is that it gives us all these test results at once. We have to know which ones is the best to look at in our scenario. Although not applicable in this dataset, if we had a small sample size we could use the Fisher’s exact test results above as well.
Tests of association are best designed for just that, testing the existence of an association between two categorical variables. However, hypothesis tests are impacted by sample size. When we have the same sample size, tests of association can rank significance of variables with p-values. However, when sample sizes are not the same (or degrees of freedom are not the same) between two tests, the tests of association are not best for comparing the strength of an association. In those scenarios, we have measures of strength of association that can be compared across any sample size.
Measures of association were not designed to test if an association exists, as that is what statistical testing is for. They are designed to measure the strength of association. There are dozens of these measures. Three of the most common are the following: - Odds Ratios (only for comparing two binary variables) - Cramer’s V (able to compare nominal variables with any number of categories) - Spearman’s Correlation (able to compare ordinal variables with any number of categories).
An odds ratio indicates how much more likely, with respect to odds, a certain event occurs in one group relative to its occurrence in another group. The odds of an event occurring is not the same as the probability that an event occurs. The odds of an event occurring is the probability the event occurs divided by the probability that event does not occur.
\[ Odds = \frac{p}{1-p} \]
Let’s again examine the cross-tabulation table between central air and bonus eligibility.
Cell Contents
|-------------------------|
| N |
| Chi-square contribution |
| N / Row Total |
| N / Col Total |
| N / Table Total |
|-------------------------|
Total Observations in Table: 2051
| train$Bonus
train$Central_Air | 0 | 1 | Row Total |
------------------|-----------|-----------|-----------|
N | 142 | 5 | 147 |
| 35.112 | 50.620 | |
| 0.966 | 0.034 | 0.072 |
| 0.117 | 0.006 | |
| 0.069 | 0.002 | |
------------------|-----------|-----------|-----------|
Y | 1069 | 835 | 1904 |
| 2.711 | 3.908 | |
| 0.561 | 0.439 | 0.928 |
| 0.883 | 0.994 | |
| 0.521 | 0.407 | |
------------------|-----------|-----------|-----------|
Column Total | 1211 | 840 | 2051 |
| 0.590 | 0.410 | |
------------------|-----------|-----------|-----------|
Let’s look at the row without central air. The probability that a home without central air is not bonus eligible is 96.6%. That implies that the odds of not being bonus eligible in homes without central air is 28.41 (= 0.966/0.034). For homes with central air, the odds of not being bonus eligible are 1.28 (= 0.561/0.439). The odds ratio between these two would be approximately 22.2 (= 28.41/1.28). In other words, homes without central air are 22.2 times as likely (in terms of odds) to not be bonus eligible as compared to homes with central air. This relationship is intuitive based on the numbers we have seen. Without going into details, it can also be shown that homes with central air are 22.2 times as likely (in terms of odds) to be bonus eligible.
Cramer’s V is another measure of strength of association. Cramer’s V is calculated as follows:
\[ V = \sqrt{\frac{\chi^2_P/n}{\min(Rows-1, Columns-1)}} \]
Cramer’s V is bounded between 0 and 1 for every comparison other than two binary variables. For two binary variables being compared the bounds are -1 to 1. The idea is still the same for both. The further the value is from 0, the stronger the relationship. Unfortunately, unlike \(R^2\), Cramer’s V has no interpretative value. It can only be used for comparison.
Lastly, we have Spearman’s correlation. Much like the Mantel-Haenszel test of association was specifically designed for comparing two ordinal variables, Spearman correlation measures the strength of association between two ordinal variables. Spearman is not limited to only categorical data analysis as it is also used for detecting heteroskedasticity in linear regression. Remember, Spearman correlation is a correlation on the ranks of the observations as compared to the actual values of the observations.
As previously mentioned, these are only a few of the dozens of different measures of association that exist. However, they are the most used ones.
Let’s see how to do this in each of our softwares!
We can use the OddsRatio function to get the odds ratio.
This is the odds ratio of the left column odds in the top row over the left column odds in the bottom row. This means that homes without central air are 22.2 times as likely (in terms of odds) to not be bonus eligible as compared to homes with central air.
We use the assocstats function to get the Cramer’s V value. This function also provides the Pearson and Likelihood Ratio \(\chi^2\) tests as well.
X^2 df P(> X^2)
Likelihood Ratio 121.499 1 0
Pearson 92.351 1 0
Phi-Coefficient : 0.212
Contingency Coeff.: 0.208
Cramer's V : 0.212 The Cramer’s V value is 0.212. There is no good or bad value for Cramer’s V. There is only better or worse when comparing to another variable. For example, when looking at the relationship between the lot shape of the home and bonus eligibility, the Cramer’s V is 0.31. This would mean that lot shape has a stronger association with bonus eligibility than central air.
X^2 df P(> X^2)
Likelihood Ratio 197.36 3 0
Pearson 197.07 3 0
Phi-Coefficient : NA
Contingency Coeff.: 0.296
Cramer's V : 0.31 The cor.test function that gave us Pearson’s correlation also provides Spearman’s correlation. Since these variables are both ordinal (all binary variables are ordinal), Spearman’s correlation would be more appropriate than Cramer’s V.
Spearman's rank correlation rho
data: as.numeric(ordered(train$Central_Air)) and as.numeric(ordered(train$Bonus))
S = 1132826666, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.2121966 Again, as with Cramer’s V, Spearman’s correlation is a comparison metric, not a good vs. bad metric. For example, when looking at the relationship between the number of fireplaces of the home and bonus eligibility, the Spearman’s correlation is 0.43. This would mean that fireplace count has a stronger association with bonus eligibility than central air.
Spearman's rank correlation rho
data: as.numeric(ordered(train$Fireplaces)) and as.numeric(ordered(train$Bonus))
S = 824354870, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.4267176 We can use the fisher_exact function from above to also get the odds ratio. The statistic that is reported in the output is the odds ratio between the two binary variables.
SignificanceResult(statistic=22.18334892422825, pvalue=1.0365949500671678e-27)This is the odds ratio of the left column odds in the top row over the left column odds in the bottom row. This means that homes without central air are 22.2 times as likely (in terms of odds) to not be bonus eligible as compared to homes with central air.
The association function from scipy.stats.contingency gives us the Cramer’s V value with the method = "cramer" option.
0.21219662657018892The Cramer’s V value is 0.212. There is no good or bad value for Cramer’s V. There is only better or worse when comparing to another variable. For example, when looking at the relationship between the lot shape of the home and bonus eligibility, the Cramer’s V is 0.31. This would mean that lot shape has a stronger association with bonus eligibility than central air.
0.3099793602802267The spearmanr function provides Spearman’s correlation. Since these variables are both ordinal (all binary variables are ordinal), Spearman’s correlation would be more appropriate than Cramer’s V.
SignificanceResult(statistic=0.21219662657018892, pvalue=2.604243816433701e-22)Again, as with Cramer’s V, Spearman’s correlation is a comparison metric, not a good vs. bad metric. For example, when looking at the relationship between the number of fireplaces of the home and bonus eligibility, the Spearman’s correlation is 0.43. This would mean that fireplace count has a stronger association with bonus eligibility than central air.
The FREQ procedure provides us with the necessary measures of association as well with the right options. Again, we are just changing the options in the TABLES statement. We keep the chisq option to get the Cramer’s V value, but also provide the measures option to get Spearman as well as the Odds Ratio table. The cl option just provides confidence intervals around these measures.
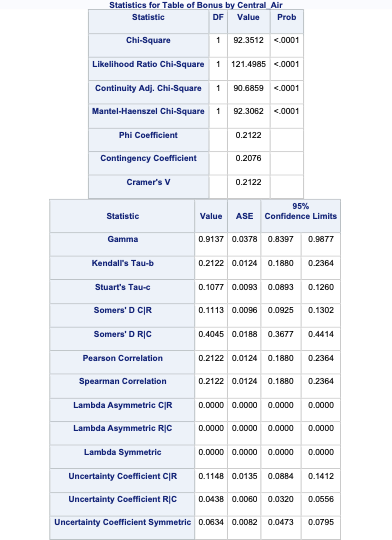
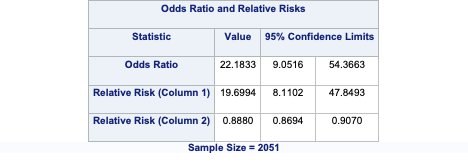
Let’s examine the odds ratio first. This is the odds ratio of the left column odds in the top row over the left column odds in the bottom row. This means that homes without central air are 22.2 times as likely (in terms of odds) to not be bonus eligible as compared to homes with central air.
The Cramer’s V value is 0.212. There is no good or bad value for Cramer’s V. There is only better or worse when comparing to another variable. For example, when looking at the relationship between the lot shape of the home and bonus eligibility, the Cramer’s V is 0.31. This would mean that lot shape has a stronger association with bonus eligibility than central air.
However, since these variables are both ordinal (all binary variables are ordinal), Spearman’s correlation would be more appropriate than Cramer’s V. The Spearman correlation is also 0.212. Again, as with Cramer’s V, Spearman’s correlation is a comparison metric, not a good vs. bad metric. For example, when looking at the relationship between the number of fireplaces of the home and bonus eligibility, the Spearman’s correlation is 0.43. This would mean that fireplace count has a stronger association with bonus eligibility than central air.
---
title: "Categorical Data Analysis"
format:
html:
code-fold: show
code-tools: true
editor: visual
---
# Exploratory Data Analysis
First, we need to first explore our data before building any models to try and explain/predict our categorical target variable. With categorical variables, we can look at the distribution of the categories as well as see if this distribution has any association with other variables. For this analysis we are going to the popular Ames housing dataset. This dataset contains information on home values for a sample of nearly 3,000 houses in Ames, Iowa in the early 2000s. To access this data, we first add the `AmesHousing` package and create the nicely formatted data with the `make_ordinal_ames()` function.
```{r}
library(AmesHousing)
ames <- make_ordinal_ames()
```
Imagine you worked for a real estate agency and got a bonus check if you sold a house above \$175,000 in value. Let's create this variable in our data:
```{r}
#| message: false
#| warning: false
library(tidyverse)
ames <- ames %>%
mutate(Bonus = ifelse(Sale_Price > 175000, 1, 0))
```
Before exploring any relationships between predictor variables and the target variable `Bonus`, we need to split our dataset into training and testing pieces. Because models are prone to discovering small, spurious patterns on the data that is used to create them (the training data), we set aside the validation and/or testing data to get a clear view of how they might perform on new data that the models have never seen before.
```{r}
set.seed(123)
ames <- ames %>% mutate(id = row_number())
train <- ames %>% sample_frac(0.7)
test <- anti_join(ames, train, by = 'id')
```
You are interested in what variables might be associated with obtaining a higher chance of getting a bonus (selling a house above \$175,000). An association exists between two categorical variables if the distribution of one variable changes when the value of the other categorical variable changes. If there is no association, the distribution of the first variable is the same regardless of the value of the other variable. For example, if we wanted to know if obtaining a bonus on selling a house in Ames, Iowa was associated with whether the house had central air we could look at the distribution of bonus eligible houses. If we observe that 42% of homes with central air are bonus eligible and 42% of homes without central air are bonus eligible, then it appears that central air has no bearing on whether the home is bonus eligible. However, if instead we observe that only 3% of homes without central air are bonus eligible, but 44% of home with central air are bonus eligible, then it appears that having central air might be related to a home being bonus eligible.
To understand the distribution of categorical variables we need to look at frequency tables. A frequency table shows the number of observations that occur in certain categories or intervals. A one-way frequency table examines all the categories of one variable. These are easily visualized with bar charts.
Let's see how to do this in each of our softwares!
::: {.panel-tabset .nav-pills}
## R
Let's look at the distribution of both bonus eligibility and central air using the `table` function. The `ggplot` function with the `geom_bar` function allows us to view our data in a bar chart.
```{r}
table(train$Bonus)
ggplot(data = train) +
geom_bar(mapping = aes(x = Bonus))
```
```{r}
table(train$Central_Air)
ggplot(data = train) +
geom_bar(mapping = aes(x = Central_Air))
```
Frequency tables show single variables, but if we want to explore two variables together we look at **cross-tabulation** tables. A cross-tabulation table shows the number of observations for each combination of the row and column variables.
Let's again examine bonus eligibility, but this time across levels of central air. Again, we can use the `table` function. The `prop.table` function allows us to compare two variables in terms of proportions instead of frequencies.
```{r}
table(train$Central_Air, train$Bonus)
prop.table(table(train$Central_Air, train$Bonus))
ggplot(data = train) +
geom_bar(mapping = aes(x = Bonus, fill = Central_Air))
```
From the above output we can see that 147 homes have no central air with only 5 of them being bonus eligible. However, there are 1904 homes that have central air with 835 of them being bonus eligible. For an even more detailed breakdown we can use the `CrossTable` function.
```{r}
library(gmodels)
CrossTable(train$Central_Air, train$Bonus, prop.chisq = FALSE, expected = TRUE)
```
The advantage of the `CrossTable` function is that we can easily get not only the frequencies, but the cell, row, and column proportions. For example, the third number in each cell gives us the row proportion. For homes without central air, 96.6% of them are not bonus eligible, while 3.4% of them are. For homes with central air, 56.1% of the homes are not bonus eligible, while 43.9% of them are. This would appear that the distribution of bonus eligible homes changes across levels of central air - a relationship between the two variables. This expected relationship needs to be tested statistically for verification. The `expected = TRUE` option provides an expected cell count for each cell. These expected counts help calculate the tests of association in the next section.
## Python
To make sure we have the same train and test datasets in Python, we can use the following code to bring the datasets from R into Python (using R Studio). If we were to randomly sample the original data (even with setting a seed), R and Python would select different observations which makes it hard to compare results.
```{python}
import pandas as pd
train = r.train
test = r.test
train.shape
test.shape
```
Let's look at the distribution of both bonus eligibility and central air using the `value_counts` attribute of the `train` dataset. The `countplot` function allows us to view our data in a bar chart.
```{python}
from matplotlib import pyplot as plt
import seaborn as sns
train['Bonus'].value_counts()
ax = sns.countplot(x = "Bonus", data = train, color = "blue")
ax.set(xlabel = 'Bonus Eligible',
ylabel = 'Frequency',
title = 'Bar Graph of Bonus Eligibility')
plt.show()
```
```{python}
train['Central_Air'].value_counts()
plt.cla()
ax = sns.countplot(x = "Central_Air", data = train, color = "blue")
ax.set(xlabel = 'Central Air',
ylabel = 'Frequency',
title = 'Bar Graph of Central Air Availability')
plt.show()
```
Frequency tables show single variables, but if we want to explore two variables together we look at **cross-tabulation** tables. A cross-tabulation table shows the number of observations for each combination of the row and column variables.
Let's again examine bonus eligibility, but this time across levels of central air. Here, we can use the `crosstab` function from `pandas`.
```{python}
import pandas as pd
pd.crosstab(index = train['Central_Air'], columns = train['Bonus'])
```
```{python}
plt.cla()
ax = sns.countplot(x = "Bonus", data = train, hue = "Central_Air")
ax.set(xlabel = 'Central Air',
ylabel = 'Frequency',
title = 'Bar Graph of Central Air Availability')
plt.show()
```
From the above output we can see that 147 homes have no central air with only 5 of them being bonus eligible. However, there are 1904 homes that have central air with 835 of them being bonus eligible.
## SAS
Let's look at the distribution of both bonus eligibility and central air using the FREQ procedure. The TABLES statement will build us frequency tables on any set of variables. Here we list the variables *Bonus*, *Central_Air*, and the **cross-tabulation** between *Bonus* and *Central_Air* using the `*` notation between them. Frequency tables show single variables, but if we want to explore two variables together we look at **cross-tabulation** tables. A cross-tabulation table shows the number of observations for each combination of the row and column variables. The `plots` option allows us to look at the frequency plot of each of these with the scale changed to percentages instead of the default of raw counts.
```{r}
#| eval: false
proc freq data=logistic.ames_train;
tables Bonus Central_Air Bonus*Central_Air /
plots(only)=freqplot(scale = percent);
run;
```
{fig-align="center" width="6in"}
{fig-align="center" width="6.67in"}
{fig-align="center" width="6in"}
{fig-align="center"}
{fig-align="center" width="6in"}
{fig-align="center"}
From the above output we can see that 147 homes have no central air with only 5 of them being bonus eligible. However, there are 1904 homes that have central air with 835 of them being bonus eligible.
The advantage of the FREQ procedure in SAS is that we can easily get not only the frequencies, but the cell, row, and column proportions. For example, the fourth number in each cell gives us the column proportion. For homes without central air, 96.6% of them are not bonus eligible, while 3.4% of them are. For homes with central air, 56.1% of the homes are not bonus eligible, while 43.9% of them are. This would appear that the distribution of bonus eligible homes changes across levels of central air - a relationship between the two variables. This expected relationship needs to be tested statistically for verification. We can also use the `expected` option in the TABLES statement to provide an expected cell count for each cell. These expected counts help calculate the tests of association in the next section.
:::
# Tests of Association
We have statistical tests to evaluate relationships between two categorical variables. The null hypothesis for these statistical tests is that the two variables have no association - the distribution of one variable does not change across levels of another variable. The alternative hypothesis is an association between the two variables - the distribution of one variable changes across levels of another variable.
These statistical tests follow a $\chi^2$-distribution. The $\chi^2$-distribution is a distribution that has the following characteristics:
- Bounded below by 0
- Right skewed
- One set of degrees of freedom
A plot of a variety of $\chi^2$-distributions is shown here:
```{r echo=FALSE}
data.frame(f = 0:1500 / 100) %>%
mutate(df_1 = dchisq(x = f, df = 1),
df_2 = dchisq(x = f, df = 2),
df_3 = dchisq(x = f, df = 3),
df_5 = dchisq(x = f, df = 5),
df_10 = dchisq(x = f, df = 10)) %>%
gather(key = "df", value = "density", -f) %>%
ggplot() +
geom_line(aes(x = f, y = density, color = df, linetype = df)) +
labs(title = "Chi-Square at Various Degrees of Freedom",
x = "Chi-Square",
y = "Density") +
xlim(0,15) + ylim(0,1) +theme_minimal()
```
Two common $\chi^2$ tests are the Pearson and Likelihood Ratio $\chi^2$ tests. They compare the observed count of observations in each cell of a cross-tabulation table to their expected count **if** there was no relationship. The expected cell count applies the overall distribution of one variable across all the levels of the other variable. For example, overall 59% of all homes are not bonus eligible. **If** that were to apply to every level of central air, then the 147 homes without central air would be expected to have 86.8 ( \$ = 147 \times 0.59 \$ ) of them would be bonus eligible while 60.2 ( \$ = 147 \times 0.41\$ ) of them would not be bonus eligible. We actually observe 142 and 5 homes for each of these categories respectively. The further the observed data is from the expected data, the more evidence we have that there is a relationship between the two variables.
The test statistic for the Pearson $\chi^2$ test is the following:
$$
\chi^2_P = \sum_{i=1}^R \sum_{j=1}^C \frac{(Obs_{i,j} - Exp_{i,j})^2}{Exp_{i,j}}
$$
From the equation above, the closer that the observed count of each cross-tabulation table cell (across all rows and columns) to the expected count, the smaller the test statistic. As with all hypothesis tests, the smaller the test statistic, the larger the p-value, implying less evidence for the alternative hypothesis.
Another common test is the Likelihood Ratio test. The test statistic for this is the following:
$$
\chi^2_L = 2 \times \sum_{i=1}^R \sum_{j=1}^C Obs_{i,j} \times \log(\frac{Obs_{i,j}}{Exp_{i,j}})
$$
The p-value comes from a $\chi^2$-distribution with degrees of freedom that equal the product of the number of rows minus one and the number of columns minus one. Both of the above tests have a sample size requirement. The sample size requirement is 80% or more of the cells in the cross-tabulation table need **expected** counts larger than 5.
For smaller sample sizes, this might be hard to meet. In those situations, we can use a more computationally expensive test called Fisher's exact test. This test calculates every possible permutation of the data being evaluated to calculate the p-value without any distributional assumptions.
Both the Pearson and Likelihood Ratio $\chi^2$ tests can handle any type of categorical variable (either ordinal, nominal, or both). However, ordinal variables provide us extra information since the order of the categories actually matters compared to nominal categories. We can test for even more with ordinal variables against other ordinal variables whether two ordinal variables have a **linear association** as compared to just a general one. An ordinal test for association is the Mantel-Haenszel $\chi^2$ test. The test statistic for the Mantel-Haenszel $\chi^2$ test is the following:
$$
\chi^2_{MH} = (n-1)r^2
$$ where $r^2$ is the Pearson correlation between the column and row variables. This test follows a $\chi^2$-distribution with only one degree of freedom.
Let's see how to do each of these tests in each of our softwares!
::: {.panel-tabset .nav-pills}
## R
Let's examine the relationship between central air and bonus eligibility with the Pearson and Likelihood Ratio tests using the `assocstats` function on our `table` object comparing `Central_Air` to `Bonus`.
```{r}
library(vcd)
assocstats(table(train$Central_Air, train$Bonus))
```
The above results shows an extremely small p-value that is below any reasonable significance level. This implies that we have statistical evidence for a relationship between having central air and bonus eligibility of homes. The p-value comes from a $\chi^2$-distribution with degrees of freedom that equal the product of the number of rows minus one and the number of columns minus one.
Since both the central air and bonus eligibility variables are binary, they are ordinal. Since they are both ordinal, we should use the Mantel-Haenszel $\chi^2$ test with the `CMHtest` function. In the main output table, the first row is the Mantel-Haenszel $\chi^2$ test.
```{r}
library(vcdExtra)
CMHtest(table(train$Central_Air, train$Bonus))$table[1,]
```
From here we can see another extremely small p-value as we saw in the earlier, more general $\chi^2$ tests.
Although not applicable in this dataset, if we had a small sample size we could use the Fisher's exact test. To perform this test we can use the `fisher.test` function.
```{r}
fisher.test(table(train$Central_Air, train$Bonus))
```
We see the same results as with the other tests because the assumptions were met for sample size.
## Python
Let's examine the relationship between central air and bonus eligibility with the Pearson and Likelihood Ratio tests using the `chi2_contingency` function on our `crosstab` object comparing *Central_Air* to *Bonus*.
```{python}
from scipy.stats import chi2_contingency
chi2_contingency(pd.crosstab(index = train['Central_Air'], columns = train['Bonus']), correction = True)
```
The above results shows an extremely small p-value that is below any reasonable significance level. This implies that we have statistical evidence for a relationship between having central air and bonus eligibility of homes. The p-value comes from a $\chi^2$-distribution with degrees of freedom that equal the product of the number of rows minus one and the number of columns minus one.
Since both the central air and bonus eligibility variables are binary, they are ordinal. Since they are both ordinal, we should use the Mantel-Haenszel $\chi^2$ test. However, at the time of writing this, Python does not have a built in function for this.
Although not applicable in this dataset, if we had a small sample size we could use the Fisher's exact test. To perform this test we can use the `fisher_exact` function.
```{python}
from scipy.stats import fisher_exact
fisher_exact(pd.crosstab(index = train['Central_Air'], columns = train['Bonus']))
```
We see the same results as with the other tests because the assumptions were met for sample size.
## SAS
Let's examine the relationship between central air and bonus eligibility with the Pearson and Likelihood Ratio tests using the same FREQ procedure with some different options. The `chisq` option gives the results of the $\chi^2$ tests. The `expected`, `cellchi2`, `nocol`, and `nopercent` options change the values provided in the cells. The expected values in each cell refer to the expected values in the calculations for the tests above. The `cellchi2` gives the calculation of the Pearson test in each cell. The `relrisk` option also provides us with odds ratios which we discuss in the next section.
```{r}
#| eval: false
proc freq data=logistic.ames_train;
tables Bonus*Central_Air /
chisq expected cellchi2 nocol nopercent relrisk;
title1 'Association with Survival';
run;
```
{fig-align="center" width="6in"}
{fig-align="center" width="6in"}
The above results shows an extremely small p-value that is below any reasonable significance level for either the Pearson (just labeled "Chi-Squared" above) or the Likelihood Ratio test. This implies that we have statistical evidence for a relationship between having central air and bonus eligibility of homes. The p-value comes from a $\chi^2$- distribution with degrees of freedom that equal the product of the number of rows minus one and the number of columns minus one.
Since both the central air and bonus eligibility variables are binary, they are ordinal. Since they are both ordinal, we should use the Mantel-Haenszel $\chi^2$ test output. The beauty of SAS is that it gives us all these test results at once. We have to know which ones is the best to look at in our scenario. Although not applicable in this dataset, if we had a small sample size we could use the Fisher's exact test results above as well.
:::
# Measures of Association
Tests of association are best designed for just that, testing the existence of an association between two categorical variables. However, hypothesis tests are impacted by sample size. When we have the same sample size, tests of association can rank significance of variables with p-values. However, when sample sizes are not the same (or degrees of freedom are not the same) between two tests, the tests of association are not best for comparing the strength of an association. In those scenarios, we have measures of strength of association that can be compared across any sample size.
Measures of association were not designed to test if an association exists, as that is what statistical testing is for. They are designed to measure the strength of association. There are dozens of these measures. Three of the most common are the following: - Odds Ratios (only for comparing two binary variables) - Cramer's V (able to compare nominal variables with any number of categories) - Spearman's Correlation (able to compare ordinal variables with any number of categories).
An **odds ratio** indicates how much more likely, with respect to **odds**, a certain event occurs in one group relative to its occurrence in another group. The odds of an event occurring is *not* the same as the probability that an event occurs. The odds of an event occurring is the probability the event occurs divided by the probability that event does not occur.
$$
Odds = \frac{p}{1-p}
$$
Let's again examine the cross-tabulation table between central air and bonus eligibility.
```{r, echo=FALSE}
CrossTable(train$Central_Air, train$Bonus)
```
Let's look at the row without central air. The probability that a home without central air is not bonus eligible is 96.6%. That implies that the odds of not being bonus eligible in homes without central air is 28.41 (= 0.966/0.034). For homes with central air, the odds of not being bonus eligible are 1.28 (= 0.561/0.439). The odds ratio between these two would be approximately 22.2 (= 28.41/1.28). In other words, homes without central air are 22.2 times as likely (in terms of odds) to not be bonus eligible as compared to homes with central air. This relationship is intuitive based on the numbers we have seen. Without going into details, it can also be shown that homes with central air are 22.2 times as likely (in terms of odds) to be bonus eligible.
**Cramer's V** is another measure of strength of association. Cramer's V is calculated as follows:
$$
V = \sqrt{\frac{\chi^2_P/n}{\min(Rows-1, Columns-1)}}
$$
Cramer's V is bounded between 0 and 1 for every comparison other than two binary variables. For two binary variables being compared the bounds are -1 to 1. The idea is still the same for both. The further the value is from 0, the stronger the relationship. Unfortunately, unlike $R^2$, Cramer's V has no interpretative value. It can only be used for comparison.
Lastly, we have Spearman's correlation. Much like the Mantel-Haenszel test of association was specifically designed for comparing two ordinal variables, Spearman correlation measures the strength of association between two ordinal variables. Spearman is not limited to only categorical data analysis as it is also used for detecting heteroskedasticity in linear regression. Remember, Spearman correlation is a correlation on the ranks of the observations as compared to the actual values of the observations.
As previously mentioned, these are only a few of the dozens of different measures of association that exist. However, they are the most used ones.
Let's see how to do this in each of our softwares!
::: {.panel-tabset .nav-pills}
## R
We can use the `OddsRatio` function to get the odds ratio.
```{r}
#| message: false
library(DescTools)
OddsRatio(table(train$Central_Air, train$Bonus))
```
This is the odds ratio of the left column odds in the top row over the left column odds in the bottom row. This means that homes without central air are 22.2 times as likely (in terms of odds) to not be bonus eligible as compared to homes with central air.
We use the `assocstats` function to get the Cramer's V value. This function also provides the Pearson and Likelihood Ratio $\chi^2$ tests as well.
```{r}
assocstats(table(train$Central_Air, train$Bonus))
```
The Cramer's V value is 0.212. There is no good or bad value for Cramer's V. There is only better or worse when comparing to another variable. For example, when looking at the relationship between the lot shape of the home and bonus eligibility, the Cramer's V is 0.31. This would mean that lot shape has a stronger association with bonus eligibility than central air.
```{r}
assocstats(table(train$Lot_Shape, train$Bonus))
```
The `cor.test` function that gave us Pearson's correlation also provides Spearman's correlation. Since these variables are both ordinal (all binary variables are ordinal), Spearman's correlation would be more appropriate than Cramer's V.
```{r}
#| warning: false
cor.test(x = as.numeric(ordered(train$Central_Air)),
y = as.numeric(ordered(train$Bonus)),
method = "spearman")
```
Again, as with Cramer's V, Spearman's correlation is a comparison metric, not a good vs. bad metric. For example, when looking at the relationship between the number of fireplaces of the home and bonus eligibility, the Spearman's correlation is 0.43. This would mean that fireplace count has a stronger association with bonus eligibility than central air.
```{r}
#| warning: false
cor.test(x = as.numeric(ordered(train$Fireplaces)),
y = as.numeric(ordered(train$Bonus)),
method = "spearman")
```
## Python
We can use the `fisher_exact` function from above to also get the odds ratio. The statistic that is reported in the output is the odds ratio between the two binary variables.
```{python}
from scipy.stats import fisher_exact
fisher_exact(pd.crosstab(index = train['Central_Air'], columns = train['Bonus']))
```
This is the odds ratio of the left column odds in the top row over the left column odds in the bottom row. This means that homes without central air are 22.2 times as likely (in terms of odds) to not be bonus eligible as compared to homes with central air.
The `association` function from `scipy.stats.contingency` gives us the Cramer's V value with the `method = "cramer"` option.
```{python}
from scipy.stats.contingency import association
association(pd.crosstab(index = train['Central_Air'], columns = train['Bonus']), method = "cramer")
```
The Cramer's V value is 0.212. There is no good or bad value for Cramer's V. There is only better or worse when comparing to another variable. For example, when looking at the relationship between the lot shape of the home and bonus eligibility, the Cramer's V is 0.31. This would mean that lot shape has a stronger association with bonus eligibility than central air.
```{python}
from scipy.stats.contingency import association
association(pd.crosstab(index = train['Lot_Shape'], columns = train['Bonus']), method = "cramer")
```
The `spearmanr` function provides Spearman's correlation. Since these variables are both ordinal (all binary variables are ordinal), Spearman's correlation would be more appropriate than Cramer's V.
```{python}
from scipy.stats import spearmanr
spearmanr(train['Central_Air'], train['Bonus'])
```
Again, as with Cramer's V, Spearman's correlation is a comparison metric, not a good vs. bad metric. For example, when looking at the relationship between the number of fireplaces of the home and bonus eligibility, the Spearman's correlation is 0.43. This would mean that fireplace count has a stronger association with bonus eligibility than central air.
```{python}
from scipy.stats import spearmanr
spearmanr(train['Fireplaces'], train['Bonus'])
```
## SAS
The FREQ procedure provides us with the necessary measures of association as well with the right options. Again, we are just changing the options in the TABLES statement. We keep the `chisq` option to get the Cramer's V value, but also provide the `measures` option to get Spearman as well as the Odds Ratio table. The `cl` option just provides confidence intervals around these measures.
```{r}
#| eval: false
proc freq data=logistic.ames_train;
tables Bonus*Central_Air /
chisq measures cl;
title1 'Association with Survival';
run;
```
{fig-align="center" width="6in"}
{fig-align="center" width="6in"}
Let's examine the odds ratio first. This is the odds ratio of the left column odds in the top row over the left column odds in the bottom row. This means that homes without central air are 22.2 times as likely (in terms of odds) to not be bonus eligible as compared to homes with central air.
The Cramer's V value is 0.212. There is no good or bad value for Cramer's V. There is only better or worse when comparing to another variable. For example, when looking at the relationship between the lot shape of the home and bonus eligibility, the Cramer's V is 0.31. This would mean that lot shape has a stronger association with bonus eligibility than central air.
However, since these variables are both ordinal (all binary variables are ordinal), Spearman's correlation would be more appropriate than Cramer's V. The Spearman correlation is also 0.212. Again, as with Cramer's V, Spearman's correlation is a comparison metric, not a good vs. bad metric. For example, when looking at the relationship between the number of fireplaces of the home and bonus eligibility, the Spearman's correlation is 0.43. This would mean that fireplace count has a stronger association with bonus eligibility than central air.
:::