One of the common concerns and questions in any model development is determining how “good” a model is or how well it performs. There are many different factors that determine this and most of them depend on the goals for the model. There are typically two different purposes for modeling - estimation and prediction. Estimation quantifies the expected change in our target variable associated with some relationship or change in the predictor variables. Prediction on the other hand is focused on predicting new target observations. However, these goals are rarely seen in isolation as most people desire a blend of these goals for their models. This section will cover many of the popular metrics for model assessment.
The first thing to remember about model assessment is that a model is only “good” in context with another model. All of these model metrics are truly model comparisons. Is an accuracy of 80% good? Depends! If the previous model used has an accuracy of 90%, then no the new model is not good. However, if the previous model used has an accuracy of 70%, then yes the model is good. Although we will show many of the calculations, at no place will we say that you must meet a certain threshold for your models to be considered “good” because these metrics are designed for comparison.
Some common model metrics are based on deviance/likelihood calculations. Three common logistic regression metrics based on these are the following:
AIC
BIC
Generalized (Nagelkerke) \(R^2\)
Without going into too much mathematical detail, the AIC is a crude, large sample approximation of leave-one-out cross validation. The BIC on the other hand favors a smaller model than the AIC as it penalizes model complexity more. In both AIC and BIC, lower values are better. However, there is no amount of lower that is better enough. Neither the AIC or BIC is necessarily better than the other however they may not always agree on the “best” model.
There are a number of “pseudo”-\(R^2\) metrics for logistic regression. Here, higher values indicate a better model. The Generalized (Nagelkerke) \(R^2\) is a metric to measure how much better a model (in terms of likelihood) is compared to the intercept only model. Therefore, we compare two models with this to see which one is “more better” than the intercept compared to the other. Essentially, they are both compared to the same baseline so whichever beats that baseline by more is the model we want. Even though it is bounded between 0 and 1, there is no interpretation to this metric like we had in linear regression.
We will be using the Ames, Iowa housing data set for this section. Let’s see how we get these metrics in each of our softwares!
R provides a lot of these metrics by default in the output of the summary function on our logistic regression objects. However, we can call them separately through the AIC, BIC, and PseudoR2 functions as well. Note the which = Nagelkerke option in the PseudoR2 function to get the correct \(R^2\) value.
library(DescTools)PseudoR2(logit.model, which ="Nagelkerke")
Nagelkerke
0.7075796
We can see from the table above what the Generalized \(R^2\) is for this model. Unlike SAS, this value has already been max-rescaled to be between 0 and 1.
Python provides a lot of these metrics by default in the output of the summary function on our logistic regression objects. However, we can call them separately through the aic, bic_llf, and pseudo_rquared functions as well. Note the pseudo_rquared function to get the pseudo \(R^2\) value in Python does not max-rescale the value to be bounded between 0 and 1 like R does. SAS provides both the max-rescaled version and the non-max-rescaled version.
We can see from the table above what the Generalized \(R^2\) is for this model.
PROC LOGISTIC gives a lot of these metrics by default in the model fit statistics table provided in the output. However, to get the Generalized \(R^2\) we must use the rsq option in the MODEL statement.
Code
ods html select ParameterEstimates FitStatistics RSquare;proc logistic data=logistic.ames_train plots(only)=(oddsratio); class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl rsq; title 'Modeling Bonus Eligibility';run;quit;
We can see from the table above what the Generalized \(R^2\) is for this model. The max-rescaled \(R^2\) value ensures that the bounds are 0 and 1 so this is the metric we use so we can compare different models.
Probability Metrics
Logistic regression is a model for predicting the probability of an event, not the occurrence of an event. Logistic regression can be used for classification as well. Good models should reflect both good metrics on probability and classification, but the importance of one over the other depends on the problem.
In this section we will focus on the probability metrics. Since we are predicting the probability of an event, we want our model to assign higher predicted probabilities to events and lower predicted probabilities to non-events.
Coefficient of Discrimination
The coefficient of discrimination (or discrimination slope) is the difference in average predicted probabilities of the actual events and non-events.
\[ D = \bar{\hat{p}}_1 - \bar{\hat{p}}_0 \]
The bigger this difference, this better our model does as separating the events and non-events through the predicted probabilities. We can also examine the histograms of these predictions for comparison as well.
Let’s see how to calculate this in each of our softwares!
It is easy to calculate the difference of the average of two vectors in R which is exactly what we are doing. First, we use the predict function to gather the predictions from our model (type = "response" to get probabilities) and put them as a new column p_hat in our data frame. From there we just isolate out the events and non-events and save them in two vectors p1 and p0. This is done by conditioning the data frame to only have rows where either Bonus == 1 or Bonus == 0. Lastly, the coefficient of discrimination is just the difference of the mean of these two vectors. A plot of the two histograms overlaid on each other is also provided for visual inspection.
Code
train$p_hat <-predict(logit.model, type ="response")p1 <- train$p_hat[train$Bonus ==1]p0 <- train$p_hat[train$Bonus ==0]coef_discrim <-mean(p1) -mean(p0)ggplot(train, aes(p_hat, fill =factor(Bonus))) +geom_density(alpha =0.7) +scale_fill_grey() +labs(x ="Predicted Probability",fill ="Outcome",title =paste("Coefficient of Discrimination = ",round(coef_discrim, 3), sep =""))
The coefficient of discrimination is the difference of the average which is reported on the top of the plot above, 0.609. We can also see the two histograms of our predictions. These histograms don’t seem to have too much overlap. There is a large group of 0’s with low probabilities and a medium sized group of 1’s with high probabilities. There is a little overlap where the model wasn’t able to predict those observations as well.
It is easy to calculate the difference of the average of two vectors in Python which is exactly what we are doing. First, we use the predict function to gather the predictions from our model and put them as a new column p_hat in our data frame. From there we just isolate out the events and non-events and save them in two vectors p1 and p0. This is done by conditioning the data frame to only have rows where either Bonus == 1 or Bonus == 0. Lastly, the coefficient of discrimination is just the difference of the mean of these two vectors. A plot of the two histograms overlaid on each other is also provided for visual inspection.
from matplotlib import pyplot as pltimport seaborn as snsax = sns.displot(data = train, x = train['p_hat'], hue ='Bonus', common_norm =False, kind ='kde', fill =True)
/Users/aric/Library/r-miniconda-arm64/envs/r-reticulate/lib/python3.9/site-packages/seaborn/_oldcore.py:1119: FutureWarning: use_inf_as_na option is deprecated and will be removed in a future version. Convert inf values to NaN before operating instead.
with pd.option_context('mode.use_inf_as_na', True):
/Users/aric/Library/r-miniconda-arm64/envs/r-reticulate/lib/python3.9/site-packages/seaborn/_oldcore.py:1075: FutureWarning: When grouping with a length-1 list-like, you will need to pass a length-1 tuple to get_group in a future version of pandas. Pass `(name,)` instead of `name` to silence this warning.
data_subset = grouped_data.get_group(pd_key)
/Users/aric/Library/r-miniconda-arm64/envs/r-reticulate/lib/python3.9/site-packages/seaborn/_oldcore.py:1075: FutureWarning: When grouping with a length-1 list-like, you will need to pass a length-1 tuple to get_group in a future version of pandas. Pass `(name,)` instead of `name` to silence this warning.
data_subset = grouped_data.get_group(pd_key)
The coefficient of discrimination is the difference of the average which is reported in the output above, 0.609. We can also see the two histograms of our predictions. These histograms don’t seem to have too much overlap. There is a large group of 0’s with low probabilities and a medium sized group of 1’s with high probabilities. There is a little overlap where the model wasn’t able to predict those observations as well.
PROC LOGISTIC doesn’t provide the coefficient of discrimination through an option. However, we can easily calculate it ourselves from the predicted probabilities. Using the OUTPUT statement, we gather the predicted probabilities for our training set as we have previously seen. PROC SORT is then used to sort these predicted probabilities for graphing purposes. Next, we use PROC TTEST. We aren’t actually interested in the t-test, but really the calculation of the mean difference between these two categories and the visual representation of the two histograms - the predicted probabilities of the events and non-events. In PROC TTEST we use the predprobs data set from PROC LOGISTIC. The CLASS statement defines the two groups we are trying to compare which is our target variable. The VAR statement defines the variable we are averaging and comparing, which is our predicted probabilities phat.
Code
proc logistic data=logistic.ames_train noprint; class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl; output out=predprobs p=phat;run;proc sort data=predprobs; by Bonus;run;proc means data=predprobs mean; by Bonus; var phat;run;proc sgplot data=predprobs; styleattrs datacolors=(darkblue darkred) datacontrastcolors=(darkblue darkred); histogram phat / group=Bonus transparency=0.5; density phat / type=kernel group=Bonus; refline 0.16/ axis=x lineattrs=(color=darkblue pattern=2thickness=2) label=('Non-Event (0)') ; refline 0.77/ axis=x lineattrs=(color=darkred pattern=2thickness=2) label=('Event (1)') labelpos=max; title 'Predicted Probabilities for Bonus Eligibility'; inset "Non-Event Average = 0.16""Event Average = 0.77""Coefficient = 0.61"/ border title="Average Predicted Probabilities" position=topright;run;
The coefficient of discrimination is the difference of the average which is reported on the table above. We can also see the two histograms of our predictions. These histograms seems to have a lot of overlap, leading us to believe that our model has a lot events and non-events with similar predicted probabilities.
Rank-Order Statistics
Rank-order statistics measure how well a model orders the predicted probabilities. Three common metrics that summarize things together are concordance, discordance, and ties. In these metrics every single combination of an event and non-event are compared against each other (1 event vs. 1 non-event). A concordant pair is a pair with the event having a higher predicted probability than the non-event - the model got the rank correct. A discordant pair is a pair with the event having a lower predicted probability than the non-event - the model got the rank wrong. A tied pair is a pair where the event and non-event have the same predicted probability - the model isn’t sure how to distinguish between them. Models with higher concordance are considered better. The interpretation on concordance is that for all possible event and non-event combinations, the model assigned the higher predicted probability to the observation with the event concordance% of the time.
There are a host of other metrics that are based on these rank-statistics such as the \(c\)-statistic, Somer’s D, and Kendall’s \(\tau_\alpha\). The calculations for these are as follows:
Although not provided immediately in the model summary, R can easily provide a couple of the metrics above with the and somers2 function.
Code
library(Hmisc)somers2(train$p_hat, train$Bonus)
C Dxy n Missing
0.9428394 0.8856789 2051.0000000 0.0000000
As we can see from the output, our model assigned the higher predicted probability to the observation with the bonus eligible home 94.3% of the time (the C in the output). Somer’s D had a value of 0.885 (the Dxy in the output). Just like with other model metrics, we cannot say whether these are “good” values of these metrics as they are meant for comparison. If these values are higher than the same values from another model, then this model is better than the other model.
Although not provided immediately in the model summary, Python can easily provide a couple of the metrics above with the somersd and kendalltau functions.
Code
from scipy.stats import somersdsomersd(train['Bonus'], train['p_hat'])
As we can see from the output, our model’s Somer’s D had a value of 0.885 and the Kendall \(\tau_\alpha\) value of 0.616. Just like with other model metrics, we cannot say whether these are “good” values of these metrics as they are meant for comparison. If these values are higher than the same values from another model, then this model is better than the other model.
SAS provides all these metrics by default in the associations table part of the PROC LOGISTIC output.
Code
ods html select Association ParameterEstimates;proc logistic data=logistic.ames_train plots(only)=(oddsratio); class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl; title 'Modeling Bonus Eligibility';run;quit;
As we can see from the output, our model assigned the higher predicted probability to the observation with the bonus eligible home 94.3% of the time.
Classification Metrics
Logistic regression is a model for predicting the probability of an event, not the occurrence of an event. Logistic regression can be used for classification as well. Good models should reflect both good metrics on probability and classification, but the importance of one over the other depends on the problem.
In this section we will focus on the classification metrics. We want a model to correctly classify events and non-events. Classification forces the model to predict either an event or non-event for each observation based on the predicted probability for that observation. For example, \(\hat{y}_1 = 1\) if \(\hat{p}_i > 0.5\). These are called cut-offs or thresholds. However, strict classification-based measures completely discard any information about the actual quality of the model’s predicted probabilities.
Many of the metrics around classification try to balance different pieces of the classification table (also called the confusion matrix). An example of one is shown below.
Classification Table Example
Let’s examine the different pieces of the classification table that people jointly focus on.
Sensitivity & Specificity
Sensitivity is the proportion of times you were able to predict an event in the groups of actual events. Of the actual events, the proportion of the time you correctly predicted an event. This is also called the true positive rate. This is also just another name for recall.
Example Calculation of Sensitivity
This is balanced typically with the specificity. Specificity is the proportion of times you were able to predict a non-event in the group of actual non-events. Of the actual non-events, the proportion of the time you correctly predicted non-event. This is also called the true negative rate.
Example Calculation of Specificity
These offset each other in a model. One could easily maximize one of these at the cost of the other. To get maximum sensitivity you can just predict every observations is an event, however this would drop your specificity to 0. The reverse is also true. Those who focus on sensitivity and specificity want balance in each. One measure for the optimal cut-off from a model is the Youden’s Index (or Youden’s J Statistic). This is easily calculated as \(J = sensitivity + specificity - 1\). The optimal cut-off for determining predicted events and non-events would be at the point where this is maximized.
Let’s see how to do this in each of our softwares!
R produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities. The table function creates the classification table for us after using the ifelse function to define our cut-off at 0.5.
We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a for loop in R. However, the measureit function can do this for us. The inputs for this function are the predicted probabilities first, followed by the target variable. The measure option allows you to define additional measures to calculate at each cut-off. In the code below we ask for accuracy (ACC), sensitivity (SENS), and specificity (SPEC). From there we combine these variables into a single dataframe and print the observations with the head function.
We could calculate the Youden Index by hand and then rank the new dataframe by this value, however, rocit function will gives this to us automatically in the next piece of code.
Another commonly used visual for the balance of sensitivity and specificity across all of the cut-offs is the Receiver Operator Characteristic curve. Commonly known as the ROC curve. The ROC curve plots the balance of sensitivity vs. specificity. The “best” ROC curve is the one that reaches to the upper left hand side of the plot as that would imply that our model has both high levels of sensitivity and specificity. The worst ROC curve is represented by the diagonal line in the plot since that would imply our model is as good as randomly assigning events and non-events to our observations. This leads some to calculate the area under the ROC curve (typically called AUC) as a metric summarizing the curve itself. The math won’t be shown here, but the AUC is equal to the \(c\)-statistic in the Rank-order statistics section. Isn’t math fun!?!?
R easily produces ROC curves from a variety of functions. A popular, new function is the rocit function. Using the plot function on the rocit object gives the ROC curve. By calling the $optimal element of the plot of the rocit object, it gives the value of the Youden’s Index (value in the output) along with the respective cut-off that corresponds to that maximum Youden value. The summary function on the rocit object will report the AUC value. We can also get confidence intervals around our AUC values (ciAUC function) and ROC curves (ciROC function).
Warning in regularize.values(x, y, ties, missing(ties), na.rm = na.rm):
collapsing to unique 'x' values
We can see that the highest Youden J statistic had a value of 0.7352. This took place at a cut-off of 0.423. Therefore, according to the Youden Index at least, the optimal cut-off for our model is 0.423. In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event. We can also see that the area under our ROC curve is 0.9428. Similar to other metrics, we cannot say whether this is a “good” value of AUC, only if it is better or worse than another model’s AUC.
Another common function is the performance function that produces many more plots than the ROC curve. Here the ROC curve is obtained by plotting the true positive rate by the false positive rate using the measure = "tpr" and "x.measure = "fpr" options. The AUC is also obtained from the performance function by calling the measure = "auc" option.
Python produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities. The crosstab function creates the classification table for us after using the map function to define our cut-off at 0.5.
Code
import pandas as pdtrain['pred'] = train['p_hat'].map(lambda x: 1if x >0.5else0)pd.crosstab(train['Bonus'], train['pred'])
pred 0 1
Bonus
0.0 1062 149
1.0 127 713
We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a for loop in Python. However, the roc_curve function can do this for us. The inputs for this function are the target variable first, followed by the predicted probabilities. We are saving the output of this function into three objects fpr (the false positive rate or \(1-specificity\)), the tpr (the true positive rate), and the corresponding threshold to get those values. From there we combine these variables into a single dataframe. We then calculate the Youden Index as the difference between the TPR and FPR. From there we sort by this Youden Index value and print the observations.
We can see that the highest Youden J statistic had a value of 0.7352. This took place at a cut-off of 0.423. Therefore, according to the Youden Index at least, the optimal cut-off for our model is 0.423. In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event.
Another commonly used visual for the balance of sensitivity and specificity across all of the cut-offs is the Receiver Operator Characteristic curve. Commonly known as the ROC curve. The ROC curve plots the balance of sensitivity vs. specificity. The “best” ROC curve is the one that reaches to the upper left hand side of the plot as that would imply that our model has both high levels of sensitivity and specificity. The worst ROC curve is represented by the diagonal line in the plot since that would imply our model is as good as randomly assigning events and non-events to our observations. This leads some to calculate the area under the ROC curve (typically called AUC) as a metric summarizing the curve itself. The math won’t be shown here, but the AUC equal to the \(c\)-statistic in the Rank-order statistics section. Isn’t math fun!?!?
Python easily produces ROC curves from the RocCurveDisplay function using the fpr and tpr objects we previously calculated in the code above. Using the plot function on this object gives the ROC curve. The auc function provides us with the AUC value for the ROC curve.
Code
RocCurveDisplay(fpr = fpr, tpr = tpr).plot()
<sklearn.metrics._plot.roc_curve.RocCurveDisplay object at 0x17ee51430>
No artists with labels found to put in legend. Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
Code
plt.show()
Code
auc(fpr, tpr)
0.9428394479178954
We can also see that the area under our ROC curve is 0.9428. Similar to other metrics, we cannot say whether this is a “good” value of AUC, only if it is better or worse than another model’s AUC.
PROC LOGISTIC produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities. The outroc option in the SCORE statement creates the classification table for us. The fitstat option defines the metrics for this classification table across the ROC curve. We want to look at all classification tables for cut-offs ranging across the whole ROC curve. Next, we use a DATA STEP to take these metrics from PROC LOGISTIC and calculate the Youden J statistic for each of the cut-offs from the given sensitivity and specificity provided by SAS. From there we use PROC SORT to rank these by this youden variable and print the first 10 observations with PROC PRINT.
Code
ods html select ParameterEstimates;proc logistic data=logistic.ames_train plots(only)=(oddsratio); class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2; score data=logistic.ames_train fitstat outroc=roc; title 'Modeling Bonus Eligibility';run;quit;data work.roc; set work.roc; cutoff = _PROB_; sensitivity = _SENSIT_; specificity =1-_1MSPEC_; youden = _SENSIT_ - _1MSPEC_;run;proc sort data=work.roc; by descending youden;run;proc print data=work.roc (obs =10);run;
We can see that the highest Youden J statistic had a value of 0.7352. This took place at a cut-off of 0.423. Therefore, according to the Youden Index at least, the optimal cut-off for our model is 0.423. In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event.
Another commonly used visual for the balance of sensitivity and specificity across all of the cut-offs is the Receiver Operator Characteristic curve. Commonly known as the ROC curve. The ROC curve plots the balance of sensitivity vs. specificity. The “best” ROC curve is the one that reaches to the upper left hand side of the plot as that would imply that our model has both high levels of sensitivity and specificity. The worst ROC curve is represented by the diagonal line in the plot since that would imply our model is as good as randomly assigning events and non-events to our observations. This leads some to calculate the area under the ROC curve (typically called AUC) as a metric summarizing the curve itself. The math won’t be shown here, but the AUC equal to the \(c\)-statistic in the Rank-order statistics section. Isn’t math fun!?!?
SAS easily produces ROC curves from PROC LOGISTIC using the plots=ROC option.
Code
ods html select ROCCurve;proc logistic data=logistic.ames_train plots(only)=ROC; class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl; title 'Modeling Bonus Eligibility';run;quit;
SAS can also compare the ROC curves across many models statistically to see if they are different based on their AUC. This is done through ROC statements. The only downside is that SAS can only compare nested versions of the model in the MODEL statement. Notice how the model in the ROC statements is just a nested version of the model in the MODEL statement. The ROCCONTRAST statement is then used with the estimate = allpairs option to statistically compare all pairs of models if more ROC statements are used.
The ROC curves in the plot above do not look different then each other visually and statistically we cannot find any differences between them based on the p-values from the tests (not shown). Therefore, we don’t need this interaction.
K-S Statistic
One of the most popular metrics for classification models in the finance and banking industry is the KS statistic. The two sample KS statistic can determine if there is a difference between two cumulative distribution functions. The two cumulative distribution functions of interest to us are the predicted probability distribution functions for the event and non-event target group. The KS \(D\) statistic is the maximum distance between these two curves - calculated by the maximum difference between the true positive and false positive rates, \(D = \max_{depth}{(TPR - FPR)} = \max_{depth}{(Sensitivity + Specificity - 1)}\). Notice, this is the same as maximizing the Youden Index.
The optimal cut-off for determining predicted events and non-events would be at the point where this \(D\) statistic (Youden Index) is maximized.
Let’s see how to do this in each of our softwares!
Using the same rocit object from the section on sensitivity and specificity (here called logit_roc) we can also calculate the KS statistic and plot the two cumulative distribution functions it represents. The ksplot function will plot the two cumulative distribution functions as well as highlight the cut-off (or threshold) where they are most separated. This point corresponds the \(D\) statistic mentioned above as well as the Youden’s Index. By calling the KS stat and KS Cutoff elements from this KS plot, we can get the optimal cut-off as well as the value at this cut-off.
Code
ksplot(logit_roc)ksplot(logit_roc)$`KS stat`
[1] 0.7352326
Code
ksplot(logit_roc)$`KS Cutoff`
[1] 0.4229724
As we saw in the previous section, the optimal cut-off according to the KS-statistic would be at 0.423. Therefore, according to the KS statistic at least, the optimal cut-off for our model is 0.423. In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event. The KS \(D\) statistic is reported as 0.7352 which is equal to the Youden’s Index value.
Another way to calculate this is by hand using the performance function we saw in the previous section as well. Using the measure = "tpr" and x.measure = "fpr" options, we can calculate the true positive rate and false positive rate across all our predictions. From there we can just use the max function to calculate the value of maximum difference between the two - the KS statistic. Finding the cut-off at this point is a little trickier with some of the needed R functions, but we essentially search the for alpha values (here the cut-offs) for the point where the KS statistic is maximized.
plot(x =unlist(perf@alpha.values), y = (1-unlist(perf@y.values)),type ="l", main ="K-S Plot (EDF)",xlab ='Cut-off',ylab ="Proportion",col ="red")lines(x =unlist(perf@alpha.values), y = (1-unlist(perf@x.values)), col ="blue")
From the output we can see the KS \(D\) statistic at 0.7352. The predicted probability that this occurs at (the optimal cut-off) is defined at 0.423 as we previously saw.
At the time of writing this code deck, Python does not have a built-in function for the KS statistic that we need. Since it is the same as the Youden’s Index, we could use the same code as the previous section and get the same results.
One thing we can replicate is the cumulative distribution function plots using the lineplot function with the hue option. However, we first need the dataset in one piece with a new variable (here called PR) that defines the positive values and negatives values to split the line plot with using the hue option. That is where the melt function comes in handy.
sns.lineplot(x ='Cut-off', y ='value', hue ='PR', data = ks_stat)plt.xlim(0, 1)
(0.0, 1.0)
Code
plt.show()
From the above plot we can see the two cumulative distribution functions as well as the Youden Index (KS \(D\) statistic) plotted on the same graph. The peak of the (KS \(D\) statistic curve) would be the optimal cut-off. Again, this value was already calculated with the Youden Index in the previous section.
The KS statistic is not limited only to logistic regression as it can estimate the difference between any two cumulative distribution functions. Therefore, we will need an additional procedure beyond PROC LOGISTIC. First, we must obtain the predicted probabilities of our training set through the OUTPUT statement of PROC LOGISTIC. We then input this data set of predictions into PROC NPAR1WAY. With the d option we can calculate the KS D statistic. The plot = edfplot option allows us to see the cumulative distributions that are being calculated. The CLASS statement defines the variable that specifies our two groups - here the target variable Bonus. The VAR statement defines the distribution calculation variable - here the predicted probabilities phat.
Code
ods html select ParameterEstimates;proc logistic data=logistic.ames_train; class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl; output out=predprobs p=phat;run;ods html select KSTest KS2Stats EDFPlot;proc npar1way data=predprobs d plot=edfplot; class Bonus; var phat;run;
From the output we can see the KS D statistic at 0.7352. The predicted probability that this occurs at (the optimal cut-off) is defined at 0.423 In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event, according to the KS statistic.
Precision & Recall
Precision and recall are another way to view a classification table from a model. Recall is the proportion of times you were able to predict an event in the groups of actual events. Of the actual events, the proportion of the time you correctly predicted an event. This is also called the true positive rate. This is also just another name for sensitivity.
Example Recall Calculation
This is balanced here with the precision. Precision is the proportion predicted events that were actually events. Of the predicted events, the proportion of the time they actually were events. This is also called the positive predictive value. Precision is growing in popularity as a balance to recall/sensitivity as compared to specificity.
Example Precision Calculation
These offset each other in a model. One could easily maximize one of these at the cost of the other. To get maximum recall you can just predict all events, however this would drop your precision. Those who focus on precision and recall want balance in each. One measure for the optimal cut-off from a model is the F1 Score. This is calculated as the following:
R produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities.
We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a for loop in R. However, the measureit function can do this for us. The inputs for this function are the predicted probabilities first, followed by the target variable. The measure option allows you to define additional measures to calculate at each cut-off. In the code below we ask for precision (PREC), sensitivity (SENS), and F1-score (FSCR). From there we combine these variables into a single dataframe and print the observations with the print function.
We can see that the highest F1 score had a value of 0.842. This took place at a cut-off of 0.423. Therefore, according to the F1 score at least, the optimal cut-off for our model is 0.423. In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event. This matches up with the Youden’s Index from above. This is not always the case. We just got lucky in this example.
Another common calculation using the precision of a model is the model’s lift. The lift of a model is simply calculated as the ratio of Precision to the population proportion of the event - \(Lift = PPV/\pi_1\). The interpretation of lift is really nice for explanation. Let’s imagine that your lift was 3 and your population proportion of events was 0.2. This means that in the top 20% of your customers, your model predicted 3 times the events as compared to you selecting people at random. Sometimes people plot lift charts where they plot the precision at all the different values of the population proportion (called depth).
Again, we can use the rocit object (called logit_roc) from earlier. The gainstable function breaks the data down into 10 groups (or buckets) ranked from highest predicted probability to lowest. We can use the plot function on this new object along with the type option to get a variety of useful plots. If you want more than 10 buckets for your data you can always use the ngroup option to specify how many you want.
Let’s examine the output above. In the first table with the data split into 10 buckets, let’s examine the first row. Here we have 205 observations (1/10 of our data, or a depth of 0.1). Remember, these observations have been ranked by predicted probability so these observations have the highest probability of being a 1 according to our model. In these 205 observations, 200 of them had the response (target value of 1) which is a response rate of 0.976. Our original data had a total response rate (proportion of 1’s) of only 0.41. This means that we did 2.382 (=0.976 / 0.41) times better than random with our top 10% of customers. Another way to think about this would be that if we were to randomly pick 10% of our data, we would have only expected to see 84 responses (target values of 1). Our best 10% had 200 responses. Again, this ratio is a value of 2.38. The table continues this calculation for each of the buckets of 10% of our data.
The lift chart displays how good that bucket is alone, while the cumulative lift chart (more popular one) displays how good you are up to that point. The cumulative lift and lift charts are the first plot displayed. The second plot is the response rate and cumulative response rate plot. Each point divided by the horizontal line at 0.41 (population response rate) gives the lift value in the first chart. The last chart is the cumulative capture rate plot. This tells us how much of the target 1’s you captured with your model. The diagonal line would be random, so the further above the line the better the model.
Another way to calculate this is the performance function in R. This can easily calculate and plot the lift chart for us using the measure = "lift" and x.measure = "rpp" options. This plots the lift vs. the rate of positive predictions.
A common place to evaluate lift is at the population proportion. In our example above, the population proportion is approximately 0.41. At that point, we have a lift of approximately 2. In other words, if we were to pick the top 41% of homes identified by our model, we would be 2 times as likely to find a bonus eligible home as compared to randomly selecting from the population. This shows the value in our model in an interpretable way.
Python produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities.
We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a for loop in Python using the precision_score, recall_score, and f1_score functions. The inputs for each function are the target variable first, followed by the predicted probabilities. We loop through many cut-off values to find the optimal F1-score.
We can see that the highest F1 score had a value of 0.842. This took place at a cut-off of 0.41. Therefore, according to the F1 score at least, the optimal cut-off for our model is 0.41. In other words, if our model predicts a probability above 0.41 then we should call this an event. Any predicted probability below 0.41 should be called a non-event. This matches up closely with the Youden’s Index from above. This is not always the case. We just got lucky in this example.
Another common calculation using the precision of a model is the model’s lift. The lift of a model is simply calculated as the ratio of Precision to the population proportion of the event - \(Lift = PPV/\pi_1\). The interpretation of lift is really nice for explanation. Let’s imagine that your lift was 3 and your population proportion of events was 0.2. This means that in the top 20% of your customers, your model predicted 3 times the events as compared to you selecting people at random. Sometimes people plot lift charts where they plot the precision at all the different values of the population proportion (called depth).
We can use the plot_lift_curve function. The inputs for the function are the target variable and the predicted probabilities of each of the 1’s and 0’s.
A common place to evaluate lift is at the population proportion. In our example above, the population proportion is approximately 0.41. At that point, we have a lift of approximately 2. In other words, if we were to pick the top 41% of homes identified by our model, we would be 2 times as likely to find a bonus eligible home as compared to randomly selecting from the population. This shows the value in our model in an interpretable way.
PROC LOGISTIC produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities. The ctable option in the MODEL statement creates the classification table for us. The pprob option defines the cut-off (or range of cut-offs) for this classification table. We want to look at all classification tables for cut-offs ranging from a predicted probability of 0 to 0.98 by steps of 0.02. Next, we use a DATA STEP to take the classification table from PROC LOGISTIC and calculate the F1 Score for each of the cut-offs from the given precision and recall provided by SAS. From there we use PROC SORT to rank these by this F1 variable and print the first 10 observations with PROC PRINT.
Code
ods html select ParameterEstimates;proc logistic data=logistic.ames_train plots(only)=(oddsratio); class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ ctable pprob =0 to 0.98 by 0.02; ods output classification=classtable; title 'Modeling Bonus Eligibility';run;quit;data classtable; set classtable; F1 =2*(PPV*Sensitivity)/(PPV+Sensitivity); drop Specificity NPV Correct;run;proc sort data=classtable; by descending F1;run;proc print data=classtable (obs =10);run;
We can see that the highest F1 score had a value of 83.68. This took place at a cut-off of 0.46. Therefore, according to the F1 score at least, the optimal cut-off for our model is 0.46. In other words, if our model predicts a probability above 0.46 then we should call this an event. Any predicted probability below 0.46 should be called a non-event.
Another common calculation using the precision of a model is the model’s lift. The lift of a model is simply calculated as the ratio of Precision to the population proportion of the event - \(Lift = PPV/\pi_1\). The interpretation of lift is really nice for explanation. Let’s imagine that your lift was 3 and your population proportion of events was 0.2. This means that in the top 20% of your customers, your model predicted 3 times the events as compared to you selecting people at random. Sometimes people plot lift charts where they plot the precision at all the different values of the population proportion (called depth).
Similar to before, we need SAS to calculate precision and recall at different cut-off values. Here we use the SCORE statement and the fitstat and outroc=roc options. This will produce the cut-offs and measures used by SAS to calculate the ROC curves. From these calculations we can derive the lift chart. Using a DATA STEP we can calculate all of the needed variables of cutoff, depth, and precision. From there we can calculate lift by using the precision as well as the population proportion of events in our low birth weight data set - here 0.3122. We then use PROC SGPLOT to plot these.
Code
proc logistic data=logistic.ames_train plots(only)=(oddsratio) noprint; class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl; score data=logistic.ames_train fitstat outroc=roc; title 'Modeling Bonus Eligibility';run;quit;data work.roc; set work.roc; cutoff = _PROB_; specif =1-_1MSPEC_; depth=(_POS_+_FALPOS_)/2051*100; precision=_POS_/(_POS_+_FALPOS_); acc=_POS_+_NEG_; lift=precision/0.4096;run;proc sgplot data=work.roc;*where 0.005<= depth <=0.50; series y=lift x=depth; refline 1.0/ axis=y; title1 "Lift Chart for Training Data"; xaxis label="Depth (%)"; yaxis label="Lift";run;quit;
A common place to evaluate lift is at the population proportion. In our example above, the population proportion is approximately 0.41. At that point, we have a lift of approximately 2. In other words, if we were to pick the top 41% of homes identified by our model, we would be 2 times as likely to find a bonus eligible home as compared to randomly selecting from the population. This shows the value in our model in an interpretable way.
Accuracy & Error
Accuracy and error rate are typically thought of when it comes to measuring the ability of a logistic regression model. Accuracy is essentially what percentage of events and non-events were predicted correctly.
Example Accuracy Calculation
The error would be the opposite of this.
Example Error Calculation
However, caution should be used with these metrics as they can easily be fooled if only focusing on them. If your data has 10% events and 90% non-events, you can easily have a 90% accurate model by guessing non-events for every observation. Instead, having less accuracy might be better if we can predict both events and non-events. These numbers are still great to report! They are just not the best to decide which model is best.
Let’s see how to do this in each of our softwares!
R produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities.
We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a for loop in R. However, the measureit function can do this for us. The inputs for this function are the predicted probabilities first, followed by the target variable. The measure option allows you to define additional measures to calculate at each cut-off. In the code below we ask for accuracy (ACC) and F1-score (FSCR). From there we combine these variables into a single dataframe and print the observations with the print function.
From the output we can see the accuracy is maximized at 86.69%. The predicted probability that this occurs at (the optimal cut-off) is defined as 0.531. In other words, if our model predicts a probability above 0.531 then we should call this an event. Any predicted probability below 0.531 should be called a non-event, according to the accuracy metric.
There is more to model building than simply maximizing overall classification accuracy. These are good numbers to report, but not necessarily to choose models on.
Python produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities.
We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a for loop in Python using the accuracy_score function. The input for the function are the target variable first, followed by the predicted probabilities. We loop through many cut-off values to find the optimal accuracy.
From the output we can see the accuracy is maximized at 86.64%. The predicted probability that this occurs at (the optimal cut-off) is defined as 0.53. In other words, if our model predicts a probability above 0.53 then we should call this an event. Any predicted probability below 0.53 should be called a non-event, according to the accuracy metric.
There is more to model building than simply maximizing overall classification accuracy. These are good numbers to report, but not necessarily to choose models on.
PROC LOGISTIC produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities. The ctable option in the MODEL statement creates the classification table for us. The pprob option defines the cut-off (or range of cut-offs) for this classification table. We want to look at all classification tables for cut-offs ranging from a predicted probability of 0 to 0.98 by steps of 0.02. From there we use PROC SORT to rank these by the Correct variable produced in PROC LOGISTIC and print the first 10 observations with PROC PRINT.
Code
ods html select Classification;proc logistic data=logistic.ames_train plots(only)=(oddsratio); class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ ctable pprob =0 to 0.98 by 0.02; ods output classification=classtable; title 'Modeling Bonus Eligibility';run;quit;proc sort data=classtable; by descending Correct;run;proc print data=classtable (obs =10);run;
From the output we can see the accuracy is maximized at 86.3%. The predicted probability that this occurs at (the optimal cut-off) is defined at 0.52. In other words, if our model predicts a probability above 0.52 then we should call this an event. Any predicted probability below 0.52 should be called a non-event, according to the accuracy metric.
There is more to model building than simply maximizing overall classification accuracy. These are good numbers to report, but not necessarily to choose models on.
Optimal Cut-off
Classification is a decision that is extraneous to statistical modeling. Although logistic regressions tend to work well in classification, it is a probability model and does not output events and non-events.
Classification assumes cost for each observation is the same, which is rarely true. It is always better to consider the costs of false positives and false negatives when considering cut-offs in classification. The previous sections talk about many ways to determine “optimal” cut-offs when costs are either not known or not necessary. However, if costs are known, they should drive the cut-off decision rather than modeling metrics that do not account for cost.
---title: "Model Assessment"format: html: code-fold: show code-tools: trueeditor: visual---```{r}#| include: false#| warning: falselibrary(AmesHousing)ames <-make_ordinal_ames()library(tidyverse)ames <- ames %>%mutate(Bonus =ifelse(Sale_Price >175000, 1, 0))set.seed(123)ames <- ames %>%mutate(id =row_number())train <- ames %>%sample_frac(0.7)test <-anti_join(ames, train, by ='id')``````{python}#| include: falsetrain = r.traintest = r.test```# Comparing ModelsOne of the common concerns and questions in any model development is determining how "good" a model is or how well it performs. There are many different factors that determine this and most of them depend on the goals for the model. There are typically two different purposes for modeling - estimation and prediction. Estimation quantifies the expected change in our target variable associated with some relationship or change in the predictor variables. Prediction on the other hand is focused on predicting new target observations. However, these goals are rarely seen in isolation as most people desire a blend of these goals for their models. This section will cover many of the popular metrics for model assessment.The first thing to remember about model assessment is that a model is only "good" in context with another model. All of these model metrics are truly model comparisons. Is an accuracy of 80% good? Depends! If the previous model used has an accuracy of 90%, then no the new model is not good. However, if the previous model used has an accuracy of 70%, then yes the model is good. Although we will show many of the calculations, at no place will we say that you must meet a certain threshold for your models to be considered "good" because these metrics are designed for comparison.Some common model metrics are based on deviance/likelihood calculations. Three common logistic regression metrics based on these are the following:1. AIC2. BIC3. Generalized (Nagelkerke) $R^2$Without going into too much mathematical detail, the AIC is a crude, large sample approximation of leave-one-out cross validation. The BIC on the other hand favors a smaller model than the AIC as it penalizes model complexity more. In both AIC and BIC, lower values are better. However, there is no amount of lower that is better enough. Neither the AIC or BIC is necessarily better than the other however they may not always agree on the "best" model.There are a number of "pseudo"-$R^2$ metrics for logistic regression. Here, higher values indicate a better model. The Generalized (Nagelkerke) $R^2$ is a metric to measure how much better a model (in terms of likelihood) is compared to the intercept only model. Therefore, we compare two models with this to see which one is "more better" than the intercept compared to the other. Essentially, they are both compared to the same baseline so whichever beats that baseline by more is the model we want. Even though it is bounded between 0 and 1, there is no interpretation to this metric like we had in linear regression.We will be using the Ames, Iowa housing data set for this section. Let's see how we get these metrics in each of our softwares!::: {.panel-tabset .nav-pills}## RR provides a lot of these metrics by default in the output of the `summary` function on our logistic regression objects. However, we can call them separately through the `AIC`, `BIC`, and `PseudoR2` functions as well. Note the `which = Nagelkerke` option in the `PseudoR2` function to get the correct $R^2$ value.```{r}#| message: falselogit.model <-glm(Bonus ~ Gr_Liv_Area +factor(House_Style) + Garage_Area + Fireplaces +factor(Full_Bath) + Lot_Area +factor(Central_Air) + TotRms_AbvGrd + Gr_Liv_Area:Fireplaces,data = train, family =binomial(link ="logit"))AIC(logit.model)BIC(logit.model)library(DescTools)PseudoR2(logit.model, which ="Nagelkerke")```We can see from the table above what the Generalized $R^2$ is for this model. Unlike SAS, this value has already been max-rescaled to be between 0 and 1.## PythonPython provides a lot of these metrics by default in the output of the `summary` function on our logistic regression objects. However, we can call them separately through the `aic`, `bic_llf`, and `pseudo_rquared` functions as well. Note the `pseudo_rquared` function to get the pseudo $R^2$ value in Python does *not* max-rescale the value to be bounded between 0 and 1 like R does. SAS provides both the max-rescaled version and the non-max-rescaled version.```{python}from statsmodels.genmod.families import Binomialfrom statsmodels.genmod.generalized_linear_model import GLMlog_model = GLM.from_formula('Bonus ~ Gr_Liv_Area + C(House_Style) + Garage_Area + Fireplaces + C(Full_Bath) + Lot_Area + C(Central_Air) + TotRms_AbvGrd + Gr_Liv_Area:Fireplaces', data = train, family = Binomial()).fit()log_model.summary()log_model.aiclog_model.bic_llflog_model.pseudo_rsquared()```We can see from the table above what the Generalized $R^2$ is for this model.## SASPROC LOGISTIC gives a lot of these metrics by default in the model fit statistics table provided in the output. However, to get the Generalized $R^2$ we must use the `rsq` option in the MODEL statement.```{r}#| eval: falseods html select ParameterEstimates FitStatistics RSquare;proc logistic data=logistic.ames_train plots(only)=(oddsratio); class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl rsq; title 'Modeling Bonus Eligibility';run;quit;```{fig-align="center" width="6in"}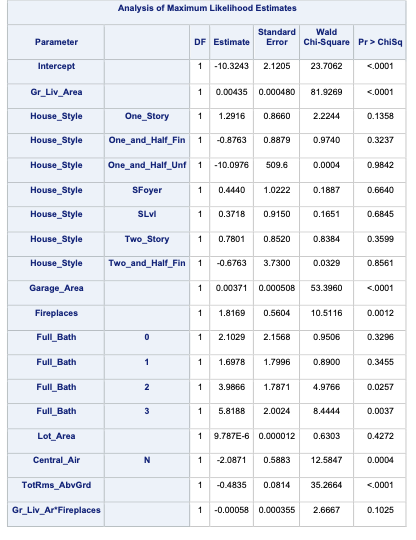{fig-align="center" width="6in"}We can see from the table above what the Generalized $R^2$ is for this model. The max-rescaled $R^2$ value ensures that the bounds are 0 and 1 so this is the metric we use so we can compare different models.:::# Probability MetricsLogistic regression is a model for predicting the **probability of an event**, not the occurrence of an event. Logistic regression **can** be used for classification as well. Good models should reflect both good metrics on probability and classification, but the importance of one over the other depends on the problem.In this section we will focus on the probability metrics. Since we are predicting the probability of an event, we want our model to assign higher predicted probabilities to events and lower predicted probabilities to non-events.## Coefficient of DiscriminationThe **coefficient of discrimination** (or discrimination slope) is the difference in average predicted probabilities of the actual events and non-events.$$ D = \bar{\hat{p}}_1 - \bar{\hat{p}}_0 $$The bigger this difference, this better our model does as separating the events and non-events through the predicted probabilities. We can also examine the histograms of these predictions for comparison as well.Let's see how to calculate this in each of our softwares!::: {.panel-tabset .nav-pills}## RIt is easy to calculate the difference of the average of two vectors in R which is exactly what we are doing. First, we use the `predict` function to gather the predictions from our model (`type = "response"` to get probabilities) and put them as a new column *p_hat* in our data frame. From there we just isolate out the events and non-events and save them in two vectors *p1* and *p0*. This is done by conditioning the data frame to only have rows where either `Bonus == 1` or `Bonus == 0`. Lastly, the coefficient of discrimination is just the difference of the mean of these two vectors. A plot of the two histograms overlaid on each other is also provided for visual inspection.```{r}train$p_hat <-predict(logit.model, type ="response")p1 <- train$p_hat[train$Bonus ==1]p0 <- train$p_hat[train$Bonus ==0]coef_discrim <-mean(p1) -mean(p0)ggplot(train, aes(p_hat, fill =factor(Bonus))) +geom_density(alpha =0.7) +scale_fill_grey() +labs(x ="Predicted Probability",fill ="Outcome",title =paste("Coefficient of Discrimination = ",round(coef_discrim, 3), sep =""))```The coefficient of discrimination is the difference of the average which is reported on the top of the plot above, 0.609. We can also see the two histograms of our predictions. These histograms don't seem to have too much overlap. There is a large group of 0's with low probabilities and a medium sized group of 1's with high probabilities. There is a little overlap where the model wasn't able to predict those observations as well.## PythonIt is easy to calculate the difference of the average of two vectors in Python which is exactly what we are doing. First, we use the `predict` function to gather the predictions from our model and put them as a new column *p_hat* in our data frame. From there we just isolate out the events and non-events and save them in two vectors *p1* and *p0*. This is done by conditioning the data frame to only have rows where either `Bonus == 1` or `Bonus == 0`. Lastly, the coefficient of discrimination is just the difference of the mean of these two vectors. A plot of the two histograms overlaid on each other is also provided for visual inspection.```{python}train['p_hat'] = log_model.predict()p1 = train[train['Bonus'] ==1]['p_hat']p0 = train[train['Bonus'] ==0]['p_hat']coef_discrim = p1.mean() - p0.mean()print(coef_discrim)``````{python}#| message: falsefrom matplotlib import pyplot as pltimport seaborn as snsax = sns.displot(data = train, x = train['p_hat'], hue ='Bonus', common_norm =False, kind ='kde', fill =True)ax.set(xlabel ='Predicted Probability', ylabel ='Density')plt.show()```The coefficient of discrimination is the difference of the average which is reported in the output above, 0.609. We can also see the two histograms of our predictions. These histograms don't seem to have too much overlap. There is a large group of 0's with low probabilities and a medium sized group of 1's with high probabilities. There is a little overlap where the model wasn't able to predict those observations as well.## SASPROC LOGISTIC doesn't provide the coefficient of discrimination through an option. However, we can easily calculate it ourselves from the predicted probabilities. Using the OUTPUT statement, we gather the predicted probabilities for our training set as we have previously seen. PROC SORT is then used to sort these predicted probabilities for graphing purposes. Next, we use PROC TTEST. We aren't actually interested in the t-test, but really the calculation of the mean difference between these two categories and the visual representation of the two histograms - the predicted probabilities of the events and non-events. In PROC TTEST we use the *predprobs* data set from PROC LOGISTIC. The CLASS statement defines the two groups we are trying to compare which is our target variable. The VAR statement defines the variable we are averaging and comparing, which is our predicted probabilities *phat*.```{r}#| eval: falseproc logistic data=logistic.ames_train noprint; class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl; output out=predprobs p=phat;run;proc sort data=predprobs; by Bonus;run;proc means data=predprobs mean; by Bonus; var phat;run;proc sgplot data=predprobs; styleattrs datacolors=(darkblue darkred) datacontrastcolors=(darkblue darkred); histogram phat / group=Bonus transparency=0.5; density phat / type=kernel group=Bonus; refline 0.16/ axis=x lineattrs=(color=darkblue pattern=2thickness=2) label=('Non-Event (0)') ; refline 0.77/ axis=x lineattrs=(color=darkred pattern=2thickness=2) label=('Event (1)') labelpos=max; title 'Predicted Probabilities for Bonus Eligibility'; inset "Non-Event Average = 0.16""Event Average = 0.77""Coefficient = 0.61"/ border title="Average Predicted Probabilities" position=topright;run;```{fig-align="center" width="6in"}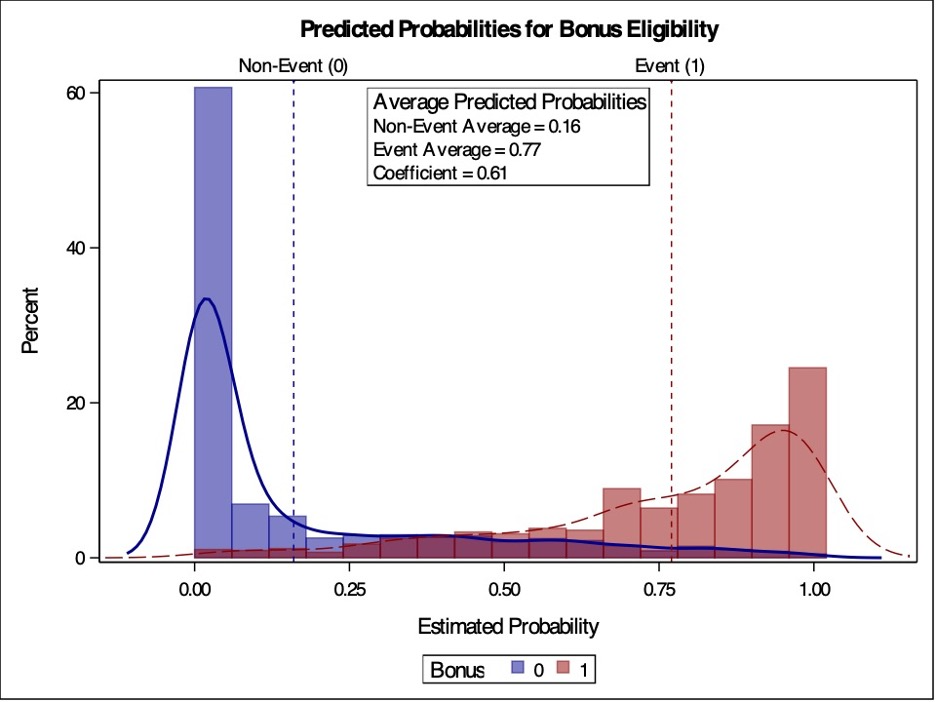{fig-align="center"}The coefficient of discrimination is the difference of the average which is reported on the table above. We can also see the two histograms of our predictions. These histograms seems to have a lot of overlap, leading us to believe that our model has a lot events and non-events with similar predicted probabilities.:::## Rank-Order StatisticsRank-order statistics measure how well a model orders the predicted probabilities. Three common metrics that summarize things together are concordance, discordance, and ties. In these metrics every single combination of an event and non-event are compared against each other (1 event vs. 1 non-event). A concordant pair is a pair with the event having a higher predicted probability than the non-event - the model got the rank correct. A discordant pair is a pair with the event having a lower predicted probability than the non-event - the model got the rank wrong. A tied pair is a pair where the event and non-event have the same predicted probability - the model isn't sure how to distinguish between them. Models with higher concordance are considered better. The interpretation on concordance is that for all possible event and non-event combinations, the model assigned the higher predicted probability to the observation with the event *concordance%* of the time.There are a host of other metrics that are based on these rank-statistics such as the $c$-statistic, Somer's D, and Kendall's $\tau_\alpha$. The calculations for these are as follows:$$ c = Concordance + 1/2\times Tied $$$$ D_{xy} = 2c - 1 $$$$ \tau_\alpha = \frac{Condorant - discordant}{0.5*n*(n-1)} $$With all of these, higher values of concordant pairs result in higher values of these metrics.Let's see how to calculate these in each of our softwares!::: {.panel-tabset .nav-pills}## RAlthough not provided immediately in the model summary, R can easily provide a couple of the metrics above with the and `somers2` function.```{r}#| message: falselibrary(Hmisc)somers2(train$p_hat, train$Bonus)```As we can see from the output, our model assigned the higher predicted probability to the observation with the bonus eligible home 94.3% of the time (the `C` in the output). Somer's D had a value of 0.885 (the `Dxy` in the output). Just like with other model metrics, we cannot say whether these are "good" values of these metrics as they are meant for comparison. If these values are higher than the same values from another model, then this model is better than the other model.## PythonAlthough not provided immediately in the model summary, Python can easily provide a couple of the metrics above with the `somersd` and `kendalltau` functions.```{python}from scipy.stats import somersdsomersd(train['Bonus'], train['p_hat'])``````{python}from scipy.stats import kendalltaukendalltau(train['Bonus'], train['p_hat'])```As we can see from the output, our model's Somer's D had a value of 0.885 and the Kendall $\tau_\alpha$ value of 0.616. Just like with other model metrics, we cannot say whether these are "good" values of these metrics as they are meant for comparison. If these values are higher than the same values from another model, then this model is better than the other model.## SASSAS provides all these metrics by default in the associations table part of the PROC LOGISTIC output.```{r}#| eval: falseods html select Association ParameterEstimates;proc logistic data=logistic.ames_train plots(only)=(oddsratio); class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl; title 'Modeling Bonus Eligibility';run;quit;```{fig-align="center" width="6in"}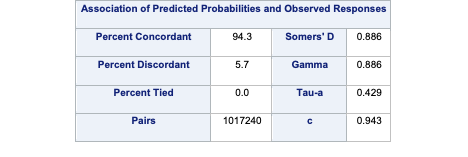{fig-align="center" width="6in"}As we can see from the output, our model assigned the higher predicted probability to the observation with the bonus eligible home 94.3% of the time.:::# Classification MetricsLogistic regression is a model for predicting the **probability of an event**, not the occurrence of an event. Logistic regression **can** be used for classification as well. Good models should reflect both good metrics on probability and classification, but the importance of one over the other depends on the problem.In this section we will focus on the classification metrics. We want a model to correctly classify events and non-events. Classification forces the model to predict either an event or non-event for each observation based on the predicted probability for that observation. For example, $\hat{y}_1 = 1$ if $\hat{p}_i > 0.5$. These are called cut-offs or thresholds. However, strict classification-based measures completely discard any information about the actual quality of the model's predicted probabilities.Many of the metrics around classification try to balance different pieces of the **classification table** (also called the **confusion matrix**). An example of one is shown below.{fig-align="center" width="5in"}Let's examine the different pieces of the classification table that people jointly focus on.## Sensitivity & SpecificitySensitivity is the proportion of times you were able to predict an event in the groups of actual events. Of the actual events, the proportion of the time you correctly predicted an event. This is also called the **true positive rate**. This is also just another name for recall.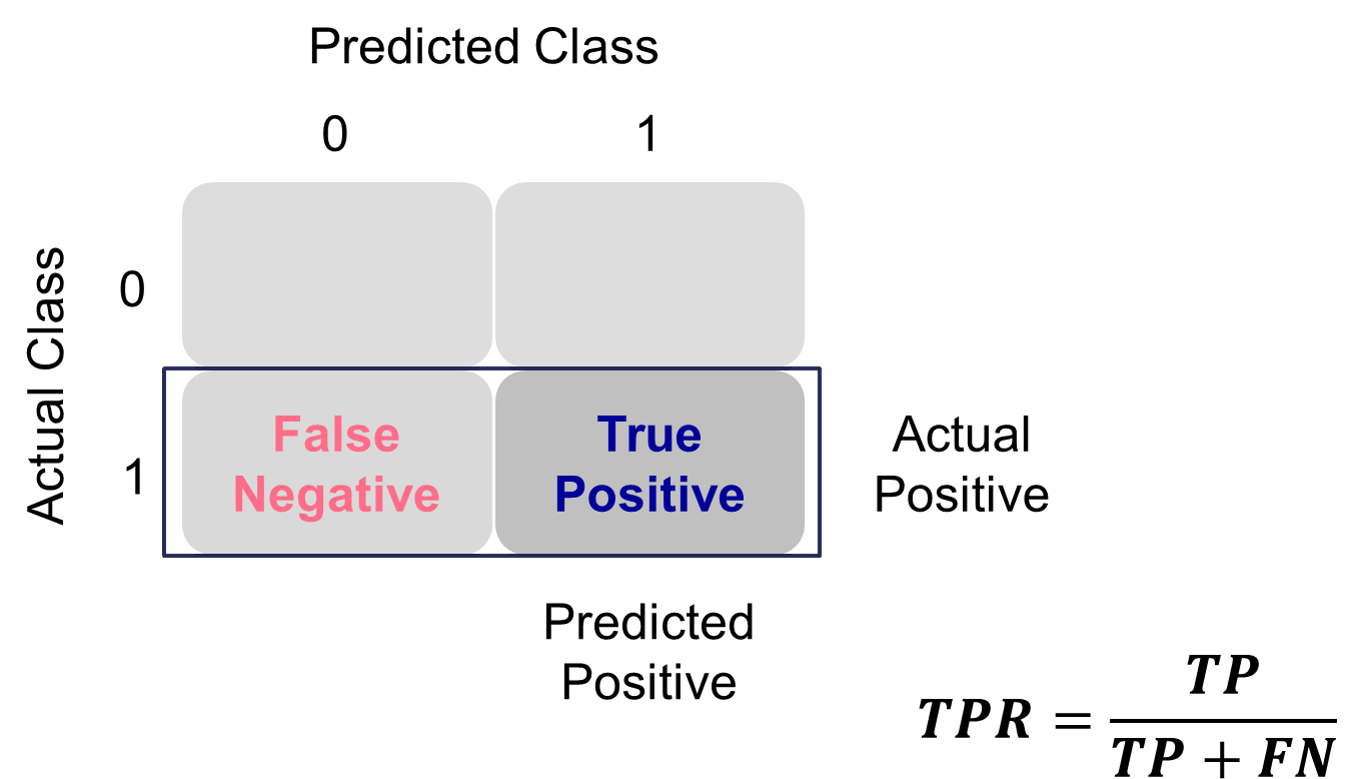{fig-align="center" width="6in"}This is balanced typically with the specificity. Specificity is the proportion of times you were able to predict a non-event in the group of actual non-events. Of the actual non-events, the proportion of the time you correctly predicted non-event. This is also called the **true negative rate**.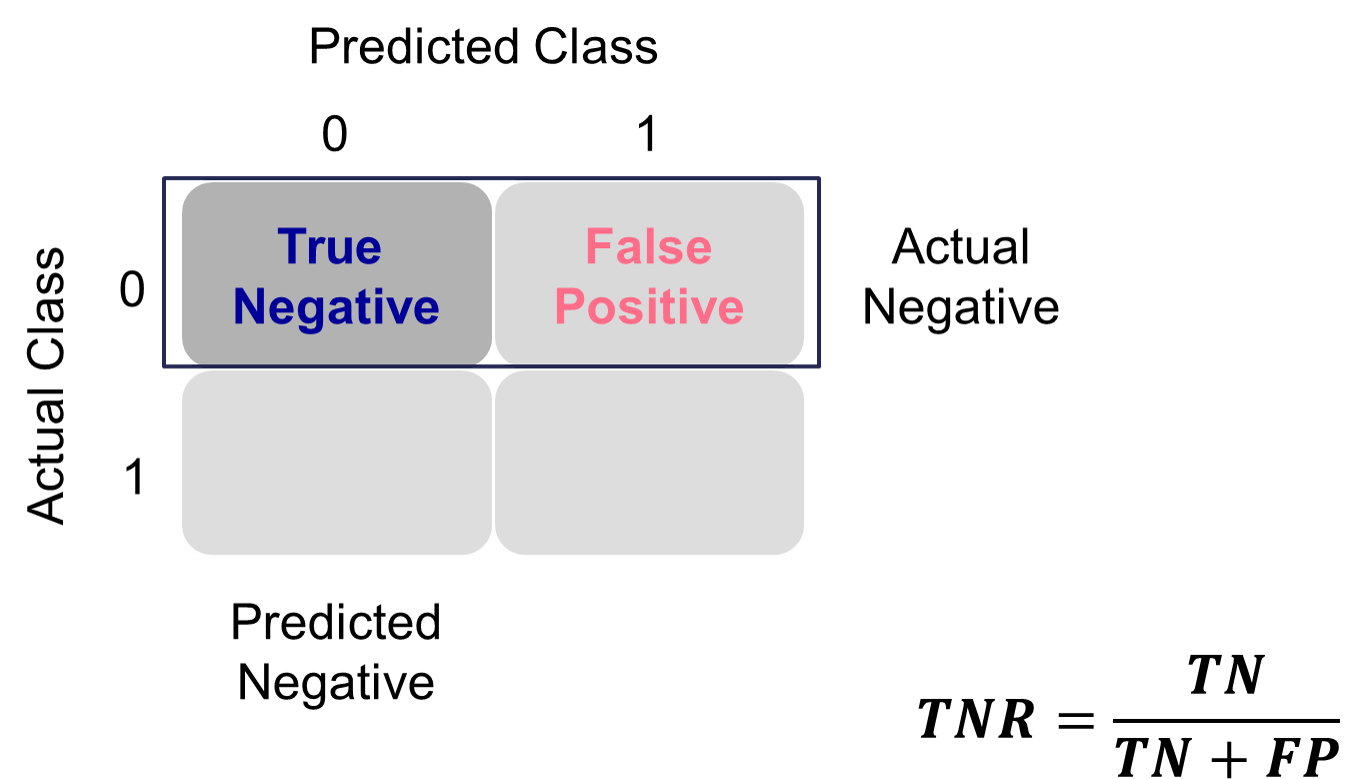{fig-align="center" width="6in"}These offset each other in a model. One could easily maximize one of these at the cost of the other. To get maximum sensitivity you can just predict every observations is an event, however this would drop your specificity to 0. The reverse is also true. Those who focus on sensitivity and specificity want balance in each. One measure for the optimal cut-off from a model is the **Youden's Index** (or Youden's J Statistic). This is easily calculated as $J = sensitivity + specificity - 1$. The optimal cut-off for determining predicted events and non-events would be at the point where this is maximized.Let's see how to do this in each of our softwares!::: {.panel-tabset .nav-pills}## RR produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities. The `table` function creates the classification table for us after using the `ifelse` function to define our cut-off at 0.5.```{r}train <- train %>%mutate(Bonus_hat =ifelse(p_hat >0.5, 1, 0))table(train$Bonus_hat, train$Bonus)```We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a `for` loop in R. However, the `measureit` function can do this for us. The inputs for this function are the predicted probabilities first, followed by the target variable. The `measure` option allows you to define additional measures to calculate at each cut-off. In the code below we ask for accuracy (`ACC`), sensitivity (`SENS`), and specificity (`SPEC`). From there we combine these variables into a single dataframe and print the observations with the `head` function.```{r}#| message: falselibrary(ROCit)logit_meas <-measureit(train$p_hat, train$Bonus, measure =c("ACC", "SENS", "SPEC"))summary(logit_meas)``````{r}youden_table <-data.frame(Cutoff = logit_meas$Cutoff, Sens = logit_meas$SENS, Spec = logit_meas$SPEC)head(youden_table, n =10)```We could calculate the Youden Index by hand and then rank the new dataframe by this value, however, `rocit` function will gives this to us automatically in the next piece of code.Another commonly used visual for the balance of sensitivity and specificity across all of the cut-offs is the Receiver Operator Characteristic curve. Commonly known as the ROC curve. The ROC curve plots the balance of sensitivity vs. specificity. The "best" ROC curve is the one that reaches to the upper left hand side of the plot as that would imply that our model has both high levels of sensitivity and specificity. The worst ROC curve is represented by the diagonal line in the plot since that would imply our model is as good as randomly assigning events and non-events to our observations. This leads some to calculate the area under the ROC curve (typically called AUC) as a metric summarizing the curve itself. The math won't be shown here, but the AUC is equal to the $c$-statistic in the Rank-order statistics section. Isn't math fun!?!?R easily produces ROC curves from a variety of functions. A popular, new function is the `rocit` function. Using the `plot` function on the `rocit` object gives the ROC curve. By calling the `$optimal` element of the plot of the `rocit` object, it gives the value of the Youden's Index (`value` in the output) along with the respective cut-off that corresponds to that maximum Youden value. The `summary` function on the `rocit` object will report the AUC value. We can also get confidence intervals around our AUC values (`ciAUC` function) and ROC curves (`ciROC` function).```{r}logit_roc <-rocit(train$p_hat, train$Bonus)plot(logit_roc)plot(logit_roc)$optimalsummary(logit_roc)ciAUC(logit_roc, level =0.99)plot(ciROC(logit_roc))```We can see that the highest Youden J statistic had a value of 0.7352. This took place at a cut-off of 0.423. Therefore, according to the Youden Index at least, the optimal cut-off for our model is 0.423. In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event. We can also see that the area under our ROC curve is 0.9428. Similar to other metrics, we cannot say whether this is a "good" value of AUC, only if it is better or worse than another model's AUC.Another common function is the `performance` function that produces many more plots than the ROC curve. Here the ROC curve is obtained by plotting the true positive rate by the false positive rate using the `measure = "tpr"` and `"x.measure = "fpr"` options. The AUC is also obtained from the `performance` function by calling the `measure = "auc"` option.```{r}library(ROCR)pred <-prediction(train$p_hat, factor(train$Bonus))perf <-performance(pred, measure ="sens", x.measure ="fpr")plot(perf, lwd =3, colorize =FALSE, colorkey =FALSE)abline(a =0, b =1, lty =3)performance(pred, measure ="auc")@y.values```## PythonPython produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities. The `crosstab` function creates the classification table for us after using the `map` function to define our cut-off at 0.5.```{python}import pandas as pdtrain['pred'] = train['p_hat'].map(lambda x: 1if x >0.5else0)pd.crosstab(train['Bonus'], train['pred'])```We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a `for` loop in Python. However, the `roc_curve` function can do this for us. The inputs for this function are the target variable first, followed by the predicted probabilities. We are saving the output of this function into three objects `fpr` (the false positive rate or $1-specificity$), the `tpr` (the true positive rate), and the corresponding threshold to get those values. From there we combine these variables into a single dataframe. We then calculate the Youden Index as the difference between the TPR and FPR. From there we sort by this Youden Index value and print the observations.```{python}from sklearn.metrics import roc_curve, auc, RocCurveDisplayfpr, tpr, thresholds = roc_curve(train['Bonus'], train['p_hat'])``````{python}data = {'TPR': tpr, 'FPR': fpr, 'Cut-off': thresholds, 'Youden': tpr-fpr}youden = pd.DataFrame(data)youden.sort_values(by = ['Youden'], ascending =False)```We can see that the highest Youden J statistic had a value of 0.7352. This took place at a cut-off of 0.423. Therefore, according to the Youden Index at least, the optimal cut-off for our model is 0.423. In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event.Another commonly used visual for the balance of sensitivity and specificity across all of the cut-offs is the Receiver Operator Characteristic curve. Commonly known as the ROC curve. The ROC curve plots the balance of sensitivity vs. specificity. The "best" ROC curve is the one that reaches to the upper left hand side of the plot as that would imply that our model has both high levels of sensitivity and specificity. The worst ROC curve is represented by the diagonal line in the plot since that would imply our model is as good as randomly assigning events and non-events to our observations. This leads some to calculate the area under the ROC curve (typically called AUC) as a metric summarizing the curve itself. The math won't be shown here, but the AUC equal to the $c$-statistic in the Rank-order statistics section. Isn't math fun!?!?Python easily produces ROC curves from the `RocCurveDisplay` function using the `fpr` and `tpr` objects we previously calculated in the code above. Using the `plot` function on this object gives the ROC curve. The `auc` function provides us with the AUC value for the ROC curve.```{python}RocCurveDisplay(fpr = fpr, tpr = tpr).plot()plt.show()``````{python}auc(fpr, tpr)```We can also see that the area under our ROC curve is 0.9428. Similar to other metrics, we cannot say whether this is a "good" value of AUC, only if it is better or worse than another model's AUC.## SASPROC LOGISTIC produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities. The `outroc` option in the SCORE statement creates the classification table for us. The `fitstat` option defines the metrics for this classification table across the ROC curve. We want to look at all classification tables for cut-offs ranging across the whole ROC curve. Next, we use a DATA STEP to take these metrics from PROC LOGISTIC and calculate the Youden J statistic for each of the cut-offs from the given sensitivity and specificity provided by SAS. From there we use PROC SORT to rank these by this *youden* variable and print the first 10 observations with PROC PRINT.```{r}#| eval: falseods html select ParameterEstimates;proc logistic data=logistic.ames_train plots(only)=(oddsratio); class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2; score data=logistic.ames_train fitstat outroc=roc; title 'Modeling Bonus Eligibility';run;quit;data work.roc; set work.roc; cutoff = _PROB_; sensitivity = _SENSIT_; specificity =1-_1MSPEC_; youden = _SENSIT_ - _1MSPEC_;run;proc sort data=work.roc; by descending youden;run;proc print data=work.roc (obs =10);run;```{fig-align="center" width="6in"}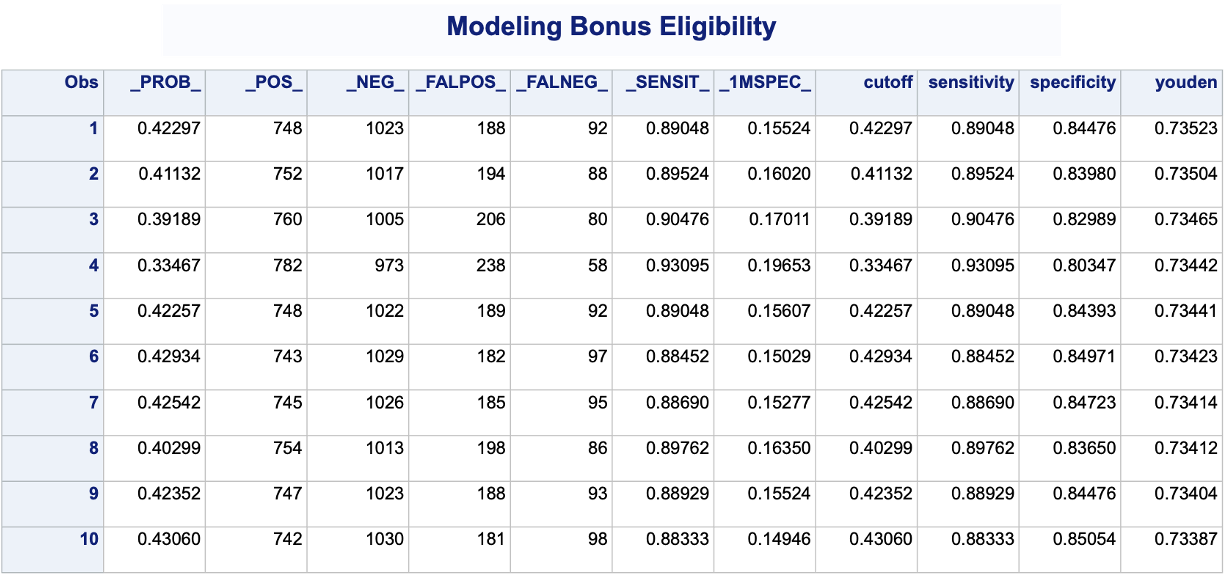{fig-align="center" width="6in"}We can see that the highest Youden J statistic had a value of 0.7352. This took place at a cut-off of 0.423. Therefore, according to the Youden Index at least, the optimal cut-off for our model is 0.423. In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event.Another commonly used visual for the balance of sensitivity and specificity across all of the cut-offs is the Receiver Operator Characteristic curve. Commonly known as the ROC curve. The ROC curve plots the balance of sensitivity vs. specificity. The "best" ROC curve is the one that reaches to the upper left hand side of the plot as that would imply that our model has both high levels of sensitivity and specificity. The worst ROC curve is represented by the diagonal line in the plot since that would imply our model is as good as randomly assigning events and non-events to our observations. This leads some to calculate the area under the ROC curve (typically called AUC) as a metric summarizing the curve itself. The math won't be shown here, but the AUC equal to the $c$-statistic in the Rank-order statistics section. Isn't math fun!?!?SAS easily produces ROC curves from PROC LOGISTIC using the `plots=ROC` option.```{r}#| eval: falseods html select ROCCurve;proc logistic data=logistic.ames_train plots(only)=ROC; class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl; title 'Modeling Bonus Eligibility';run;quit;```{fig-align="center"}SAS can also compare the ROC curves across many models statistically to see if they are different based on their AUC. This is done through ROC statements. The only downside is that SAS can only compare nested versions of the model in the MODEL statement. Notice how the model in the ROC statements is just a nested version of the model in the MODEL statement. The ROCCONTRAST statement is then used with the `estimate = allpairs` option to statistically compare all pairs of models if more ROC statements are used.```{r}#| eval: falseods html select ROCContrastEstimate ROCOverlay ROCContrastTest;proc logistic data=logistic.ames_train plots(only)=ROC; class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl; ROC 'Omit Interaction' Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd; title 'Comparing ROC Curves';run;quit;```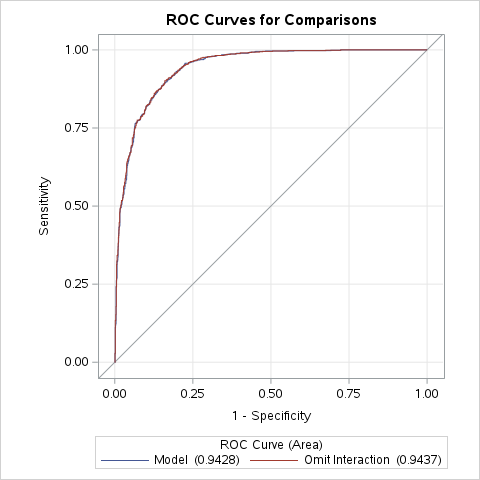{fig-align="center"}The ROC curves in the plot above do not look different then each other visually and statistically we cannot find any differences between them based on the p-values from the tests (not shown). Therefore, we don't need this interaction.:::## K-S StatisticOne of the most popular metrics for classification models in the finance and banking industry is the KS statistic. The two sample KS statistic can determine if there is a difference between two cumulative distribution functions. The two cumulative distribution functions of interest to us are the predicted probability distribution functions for the event and non-event target group. The KS $D$ statistic is the maximum distance between these two curves - calculated by the maximum difference between the true positive and false positive rates, $D = \max_{depth}{(TPR - FPR)} = \max_{depth}{(Sensitivity + Specificity - 1)}$. Notice, this is the same as maximizing the Youden Index.The optimal cut-off for determining predicted events and non-events would be at the point where this $D$ statistic (Youden Index) is maximized.Let's see how to do this in each of our softwares!::: {.panel-tabset .nav-pills}## RUsing the same `rocit` object from the section on sensitivity and specificity (here called `logit_roc`) we can also calculate the KS statistic and plot the two cumulative distribution functions it represents. The `ksplot` function will plot the two cumulative distribution functions as well as highlight the cut-off (or threshold) where they are most separated. This point corresponds the $D$ statistic mentioned above as well as the Youden's Index. By calling the `KS stat` and `KS Cutoff` elements from this KS plot, we can get the optimal cut-off as well as the value at this cut-off.```{r}ksplot(logit_roc)ksplot(logit_roc)$`KS stat`ksplot(logit_roc)$`KS Cutoff````As we saw in the previous section, the optimal cut-off according to the KS-statistic would be at 0.423. Therefore, according to the KS statistic at least, the optimal cut-off for our model is 0.423. In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event. The KS $D$ statistic is reported as 0.7352 which is equal to the Youden's Index value.Another way to calculate this is by hand using the `performance` function we saw in the previous section as well. Using the `measure = "tpr"` and `x.measure = "fpr"` options, we can calculate the true positive rate and false positive rate across all our predictions. From there we can just use the `max` function to calculate the value of maximum difference between the two - the KS statistic. Finding the cut-off at this point is a little trickier with some of the needed R functions, but we essentially search the for alpha values (here the cut-offs) for the point where the KS statistic is maximized.```{r}perf <-performance(pred, measure ="tpr", x.measure ="fpr")KS <-max(perf@y.values[[1]] - perf@x.values[[1]])cutoffAtKS <-unlist(perf@alpha.values)[which.max(perf@y.values[[1]] - perf@x.values[[1]])]print(c(KS, cutoffAtKS))plot(x =unlist(perf@alpha.values), y = (1-unlist(perf@y.values)),type ="l", main ="K-S Plot (EDF)",xlab ='Cut-off',ylab ="Proportion",col ="red")lines(x =unlist(perf@alpha.values), y = (1-unlist(perf@x.values)), col ="blue")```From the output we can see the KS $D$ statistic at 0.7352. The predicted probability that this occurs at (the optimal cut-off) is defined at 0.423 as we previously saw.## PythonAt the time of writing this code deck, Python does not have a built-in function for the KS statistic that we need. Since it is the same as the Youden's Index, we could use the same code as the previous section and get the same results.One thing we can replicate is the cumulative distribution function plots using the `lineplot` function with the `hue` option. However, we first need the dataset in one piece with a new variable (here called `PR`) that defines the positive values and negatives values to split the line plot with using the `hue` option. That is where the `melt` function comes in handy.```{python}ks_stat = youden.rename(columns = {'TPR': 'PR_T', 'FPR':'PR_F'})ks_stat = ks_stat.melt('Cut-off', var_name ='PR', value_name ='value')ks_stat.head()``````{python}sns.lineplot(x ='Cut-off', y ='value', hue ='PR', data = ks_stat)plt.xlim(0, 1)plt.show()```From the above plot we can see the two cumulative distribution functions as well as the Youden Index (KS $D$ statistic) plotted on the same graph. The peak of the (KS $D$ statistic curve) would be the optimal cut-off. Again, this value was already calculated with the Youden Index in the previous section.## SASThe KS statistic is not limited only to logistic regression as it can estimate the difference between any two cumulative distribution functions. Therefore, we will need an additional procedure beyond PROC LOGISTIC. First, we must obtain the predicted probabilities of our training set through the OUTPUT statement of PROC LOGISTIC. We then input this data set of predictions into PROC NPAR1WAY. With the `d` option we can calculate the KS D statistic. The `plot = edfplot` option allows us to see the cumulative distributions that are being calculated. The CLASS statement defines the variable that specifies our two groups - here the target variable *Bonus*. The VAR statement defines the distribution calculation variable - here the predicted probabilities *phat*.```{r}#| eval: falseods html select ParameterEstimates;proc logistic data=logistic.ames_train; class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl; output out=predprobs p=phat;run;ods html select KSTest KS2Stats EDFPlot;proc npar1way data=predprobs d plot=edfplot; class Bonus; var phat;run;```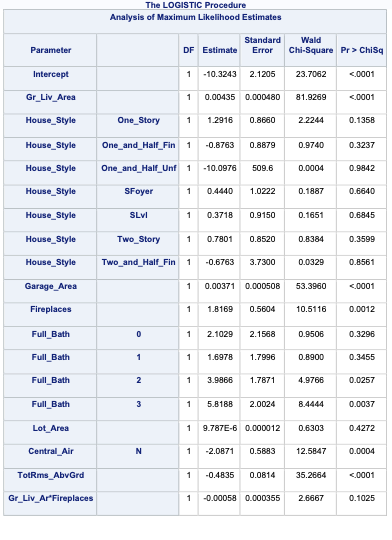{fig-align="center" width="6in"}{fig-align="center" width="6in"}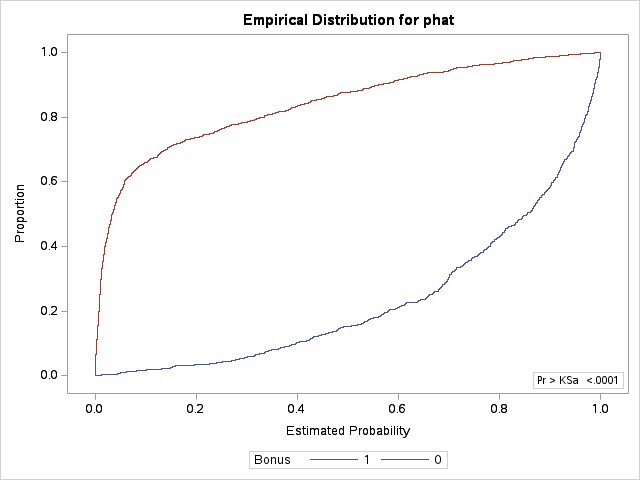{fig-align="center"}From the output we can see the KS D statistic at 0.7352. The predicted probability that this occurs at (the optimal cut-off) is defined at 0.423 In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event, according to the KS statistic.:::## Precision & RecallPrecision and recall are another way to view a classification table from a model. Recall is the proportion of times you were able to predict an event in the groups of actual events. Of the actual events, the proportion of the time you correctly predicted an event. This is also called the **true positive rate**. This is also just another name for sensitivity.{fig-align="center" width="6in"}This is balanced here with the precision. Precision is the proportion predicted events that were actually events. Of the predicted events, the proportion of the time they actually were events. This is also called the **positive predictive value**. Precision is growing in popularity as a balance to recall/sensitivity as compared to specificity.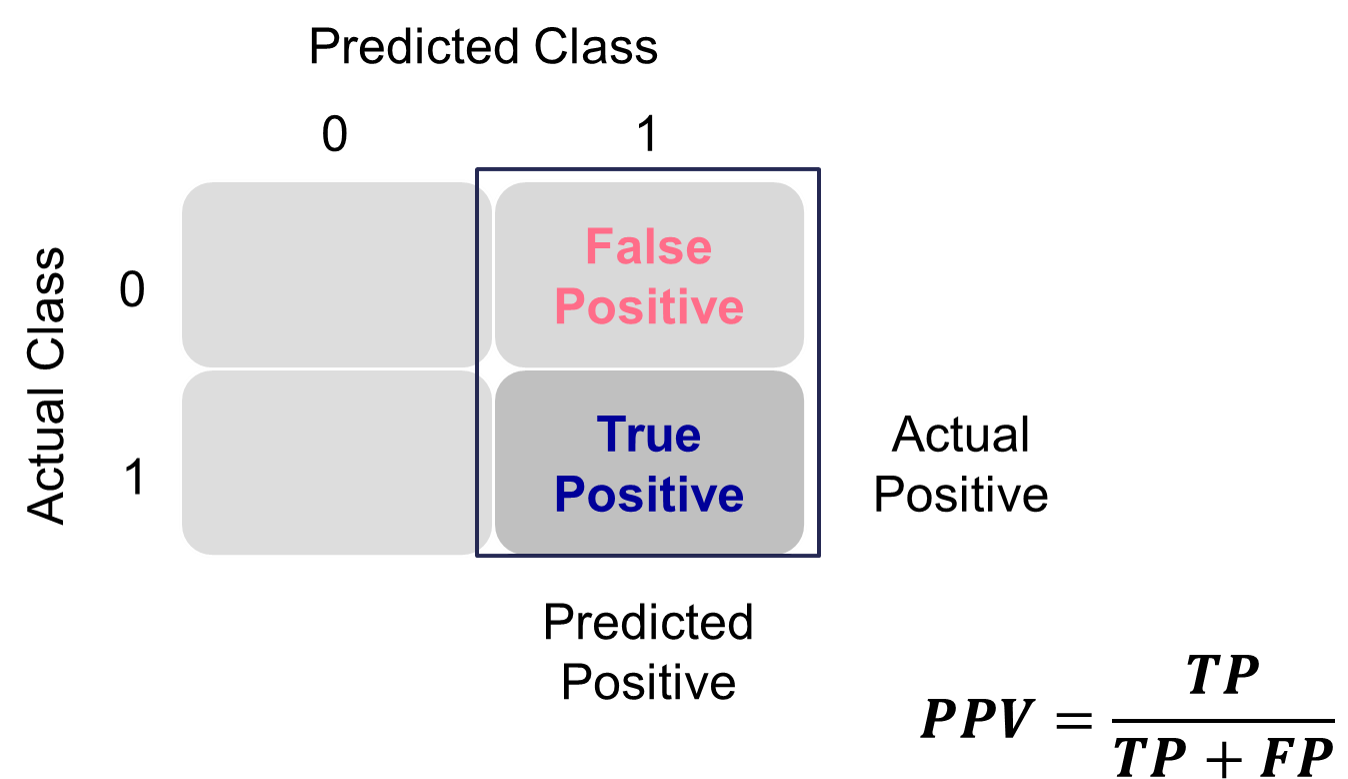{fig-align="center" width="6in"}These offset each other in a model. One could easily maximize one of these at the cost of the other. To get maximum recall you can just predict all events, however this would drop your precision. Those who focus on precision and recall want balance in each. One measure for the optimal cut-off from a model is the **F1 Score**. This is calculated as the following:$$ F_1 = 2\times \frac{precision \times recall}{precision + recall} $$The optimal cut-off for determining predicted events and non-events would be at the point where this is maximized.Let's see how to do this in each of our softwares!::: {.panel-tabset .nav-pills}## RR produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities.We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a `for` loop in R. However, the `measureit` function can do this for us. The inputs for this function are the predicted probabilities first, followed by the target variable. The `measure` option allows you to define additional measures to calculate at each cut-off. In the code below we ask for precision (`PREC`), sensitivity (`SENS`), and F1-score (`FSCR`). From there we combine these variables into a single dataframe and print the observations with the `print` function.```{r}logit_meas <-measureit(train$p_hat, train$Bonus, measure =c("PREC", "REC", "FSCR"))summary(logit_meas)fscore_table <-data.frame(Cutoff = logit_meas$Cutoff, FScore = logit_meas$FSCR)head(arrange(fscore_table, desc(FScore)), n =10)```We can see that the highest F1 score had a value of 0.842. This took place at a cut-off of 0.423. Therefore, according to the F1 score at least, the optimal cut-off for our model is 0.423. In other words, if our model predicts a probability above 0.423 then we should call this an event. Any predicted probability below 0.423 should be called a non-event. This matches up with the Youden's Index from above. This is **not** always the case. We just got lucky in this example.Another common calculation using the precision of a model is the model's **lift**. The lift of a model is simply calculated as the ratio of Precision to the population proportion of the event - $Lift = PPV/\pi_1$. The interpretation of lift is really nice for explanation. Let's imagine that your lift was 3 and your population proportion of events was 0.2. This means that in the top 20% of your customers, your model predicted 3 times the events as compared to you selecting people at random. Sometimes people plot lift charts where they plot the precision at all the different values of the population proportion (called depth).Again, we can use the `rocit` object (called `logit_roc`) from earlier. The `gainstable` function breaks the data down into 10 groups (or buckets) ranked from highest predicted probability to lowest. We can use the `plot` function on this new object along with the `type` option to get a variety of useful plots. If you want more than 10 buckets for your data you can always use the `ngroup` option to specify how many you want.```{r}logit_lift <-gainstable(logit_roc)print(logit_lift)plot(logit_lift, type =1)plot(logit_lift, type =2)plot(logit_lift, type =3)logit_lift <-gainstable(logit_roc, ngroup =15)print(logit_lift)```Let's examine the output above. In the first table with the data split into 10 buckets, let's examine the first row. Here we have 205 observations (1/10 of our data, or a depth of 0.1). Remember, these observations have been ranked by predicted probability so these observations have the highest probability of being a 1 according to our model. In these 205 observations, 200 of them had the response (target value of 1) which is a response rate of 0.976. Our original data had a total response rate (proportion of 1's) of only 0.41. This means that we did 2.382 (=0.976 / 0.41) times better than random with our top 10% of customers. Another way to think about this would be that if we were to randomly pick 10% of our data, we would have only expected to see 84 responses (target values of 1). Our **best** 10% had 200 responses. Again, this ratio is a value of 2.38. The table continues this calculation for each of the buckets of 10% of our data.The lift chart displays how good that bucket is alone, while the cumulative lift chart (more popular one) displays how good you are up to that point. The cumulative lift and lift charts are the first plot displayed. The second plot is the response rate and cumulative response rate plot. Each point divided by the horizontal line at 0.41 (population response rate) gives the lift value in the first chart. The last chart is the cumulative capture rate plot. This tells us how much of the target 1's you captured with your model. The diagonal line would be random, so the further above the line the better the model.Another way to calculate this is the `performance` function in R. This can easily calculate and plot the lift chart for us using the `measure = "lift"` and `x.measure = "rpp"` options. This plots the lift vs. the rate of positive predictions.```{r}perf <-performance(pred, measure ="lift", x.measure ="rpp")plot(perf, lwd =3, colorize =TRUE, colorkey =TRUE,colorize.palette =rev(gray.colors(256)),main ="Lift Chart for Training Data")abline(h =1, lty =3)```A common place to evaluate lift is at the population proportion. In our example above, the population proportion is approximately 0.41. At that point, we have a lift of approximately 2. In other words, if we were to pick the top 41% of homes identified by our model, we would be 2 times as likely to find a bonus eligible home as compared to randomly selecting from the population. This shows the value in our model in an interpretable way.## PythonPython produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities.We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a `for` loop in Python using the `precision_score`, `recall_score`, and `f1_score` functions. The inputs for each function are the target variable first, followed by the predicted probabilities. We loop through many cut-off values to find the optimal F1-score.```{python}from sklearn.metrics import precision_score, recall_score, f1_scoreimport numpy as npprecision = np.array([])recall = np.array([])f1score = np.array([])for y inrange(100): train['pred'] = train['p_hat'].map(lambda x: 1if x > y/100else0) value_p = precision_score(train['Bonus'], train['pred']) precision = np.append(precision, value_p) value_r = recall_score(train['Bonus'], train['pred']) recall = np.append(recall, value_r) value_f = f1_score(train['Bonus'], train['pred']) f1score = np.append(f1score, value_f)data = {'Precision': precision, 'Recall': recall, 'Cut-off': range(100), 'F1': f1score}f1_s = pd.DataFrame(data)f1_s.sort_values(by = ['F1'], ascending =False)```We can see that the highest F1 score had a value of 0.842. This took place at a cut-off of 0.41. Therefore, according to the F1 score at least, the optimal cut-off for our model is 0.41. In other words, if our model predicts a probability above 0.41 then we should call this an event. Any predicted probability below 0.41 should be called a non-event. This matches up closely with the Youden's Index from above. This is **not** always the case. We just got lucky in this example.Another common calculation using the precision of a model is the model's **lift**. The lift of a model is simply calculated as the ratio of Precision to the population proportion of the event - $Lift = PPV/\pi_1$. The interpretation of lift is really nice for explanation. Let's imagine that your lift was 3 and your population proportion of events was 0.2. This means that in the top 20% of your customers, your model predicted 3 times the events as compared to you selecting people at random. Sometimes people plot lift charts where they plot the precision at all the different values of the population proportion (called depth).We can use the `plot_lift_curve` function. The inputs for the function are the target variable and the predicted probabilities of each of the 1's and 0's.```{python}import scikitplot as skplttrain['p_hat0'] =1- train['p_hat']skplt.metrics.plot_lift_curve(y_true = train['Bonus'], y_probas = train[['p_hat0', 'p_hat']])plt.show()```A common place to evaluate lift is at the population proportion. In our example above, the population proportion is approximately 0.41. At that point, we have a lift of approximately 2. In other words, if we were to pick the top 41% of homes identified by our model, we would be 2 times as likely to find a bonus eligible home as compared to randomly selecting from the population. This shows the value in our model in an interpretable way.## SASPROC LOGISTIC produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities. The `ctable` option in the MODEL statement creates the classification table for us. The `pprob` option defines the cut-off (or range of cut-offs) for this classification table. We want to look at all classification tables for cut-offs ranging from a predicted probability of 0 to 0.98 by steps of 0.02. Next, we use a DATA STEP to take the classification table from PROC LOGISTIC and calculate the F1 Score for each of the cut-offs from the given precision and recall provided by SAS. From there we use PROC SORT to rank these by this *F1* variable and print the first 10 observations with PROC PRINT.```{r}#| eval: falseods html select ParameterEstimates;proc logistic data=logistic.ames_train plots(only)=(oddsratio); class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ ctable pprob =0 to 0.98 by 0.02; ods output classification=classtable; title 'Modeling Bonus Eligibility';run;quit;data classtable; set classtable; F1 =2*(PPV*Sensitivity)/(PPV+Sensitivity); drop Specificity NPV Correct;run;proc sort data=classtable; by descending F1;run;proc print data=classtable (obs =10);run;```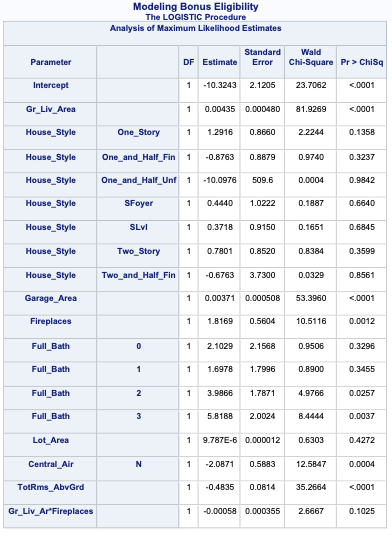{fig-align="center" width="6in"}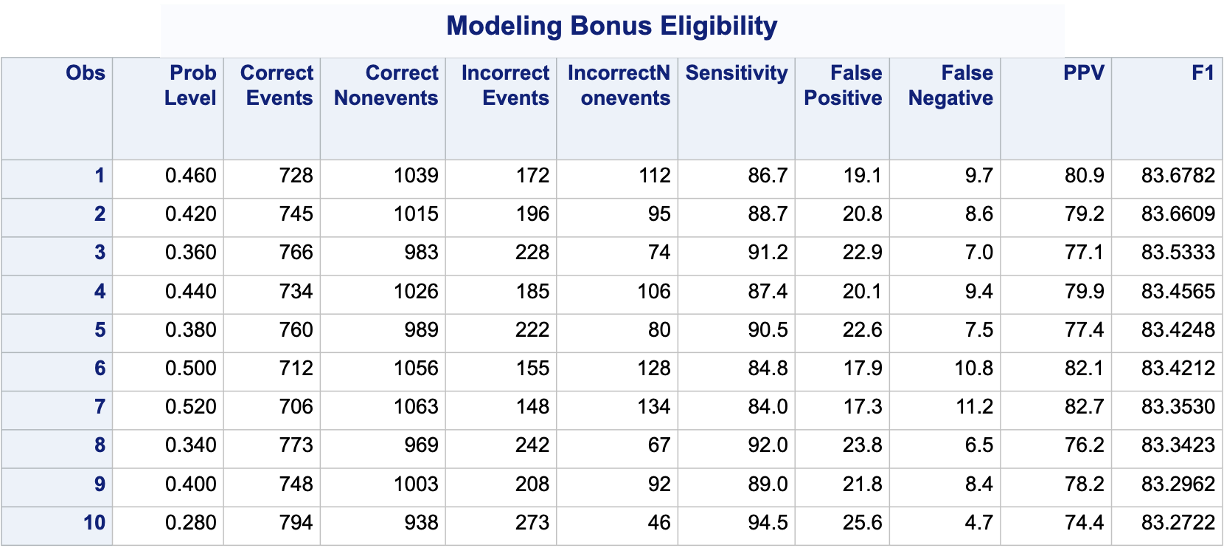{fig-align="center" width="6in"}We can see that the highest F1 score had a value of 83.68. This took place at a cut-off of 0.46. Therefore, according to the F1 score at least, the optimal cut-off for our model is 0.46. In other words, if our model predicts a probability above 0.46 then we should call this an event. Any predicted probability below 0.46 should be called a non-event.Another common calculation using the precision of a model is the model's **lift**. The lift of a model is simply calculated as the ratio of Precision to the population proportion of the event - $Lift = PPV/\pi_1$. The interpretation of lift is really nice for explanation. Let's imagine that your lift was 3 and your population proportion of events was 0.2. This means that in the top 20% of your customers, your model predicted 3 times the events as compared to you selecting people at random. Sometimes people plot lift charts where they plot the precision at all the different values of the population proportion (called depth).Similar to before, we need SAS to calculate precision and recall at different cut-off values. Here we use the SCORE statement and the `fitstat` and `outroc=roc` options. This will produce the cut-offs and measures used by SAS to calculate the ROC curves. From these calculations we can derive the lift chart. Using a DATA STEP we can calculate all of the needed variables of *cutoff*, *depth*, and *precision*. From there we can calculate lift by using the precision as well as the population proportion of events in our low birth weight data set - here 0.3122. We then use PROC SGPLOT to plot these.```{r}#| eval: falseproc logistic data=logistic.ames_train plots(only)=(oddsratio) noprint; class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ clodds=pl clparm=pl; score data=logistic.ames_train fitstat outroc=roc; title 'Modeling Bonus Eligibility';run;quit;data work.roc; set work.roc; cutoff = _PROB_; specif =1-_1MSPEC_; depth=(_POS_+_FALPOS_)/2051*100; precision=_POS_/(_POS_+_FALPOS_); acc=_POS_+_NEG_; lift=precision/0.4096;run;proc sgplot data=work.roc;*where 0.005<= depth <=0.50; series y=lift x=depth; refline 1.0/ axis=y; title1 "Lift Chart for Training Data"; xaxis label="Depth (%)"; yaxis label="Lift";run;quit;```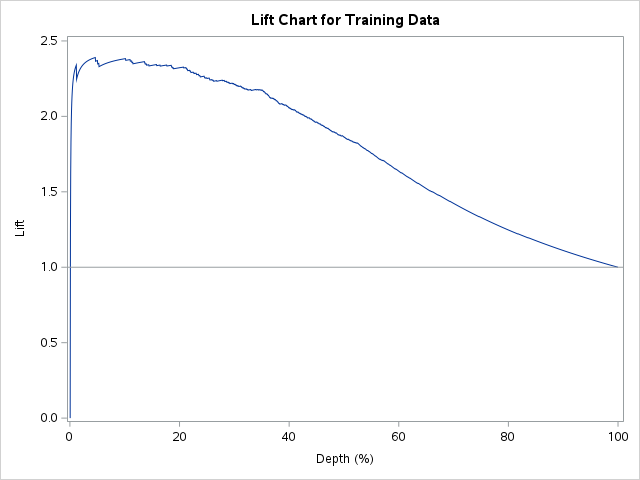{fig-align="center"}A common place to evaluate lift is at the population proportion. In our example above, the population proportion is approximately 0.41. At that point, we have a lift of approximately 2. In other words, if we were to pick the top 41% of homes identified by our model, we would be 2 times as likely to find a bonus eligible home as compared to randomly selecting from the population. This shows the value in our model in an interpretable way.:::## Accuracy & ErrorAccuracy and error rate are typically thought of when it comes to measuring the ability of a logistic regression model. Accuracy is essentially what percentage of events and non-events were predicted correctly.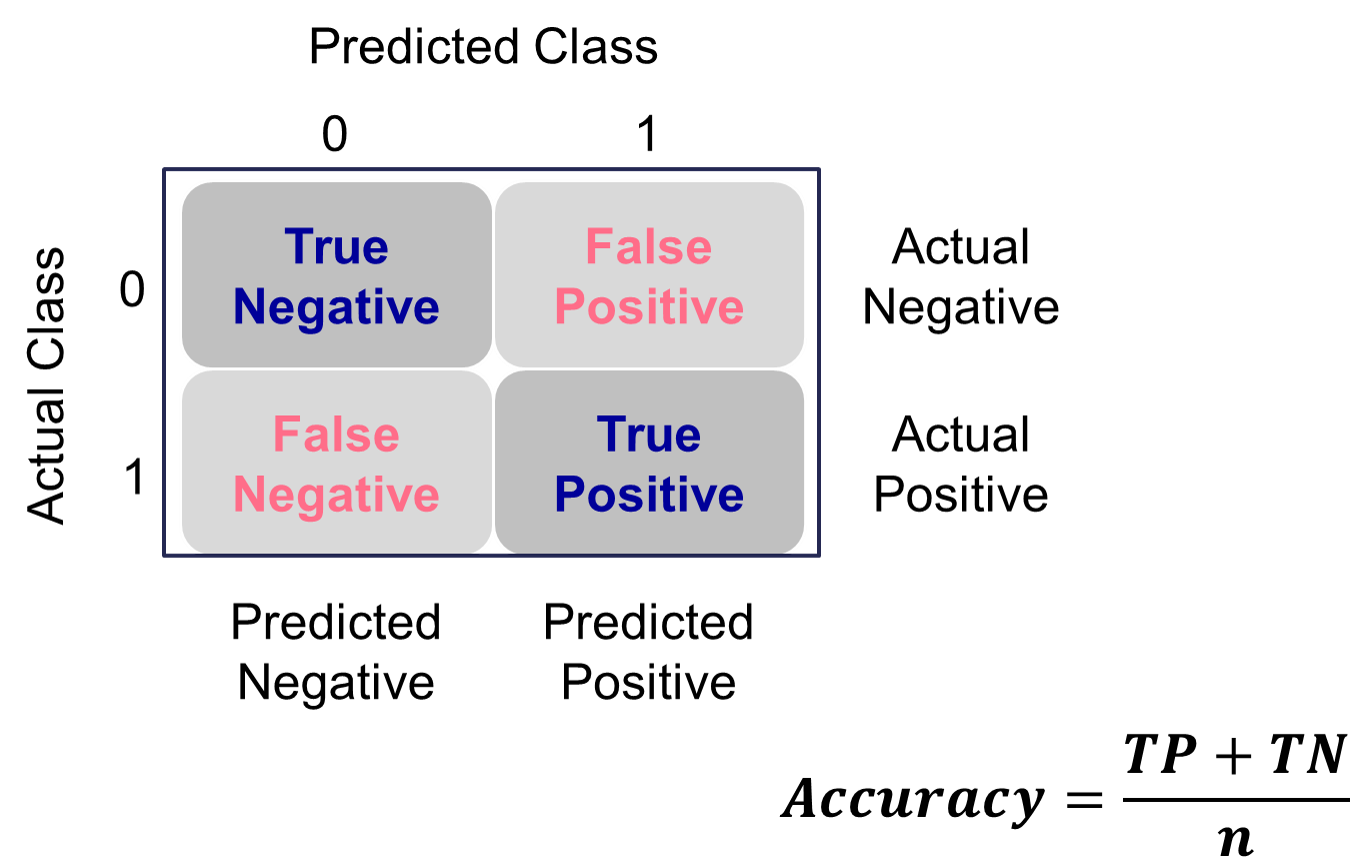{fig-align="center" width="6in"}The error would be the opposite of this.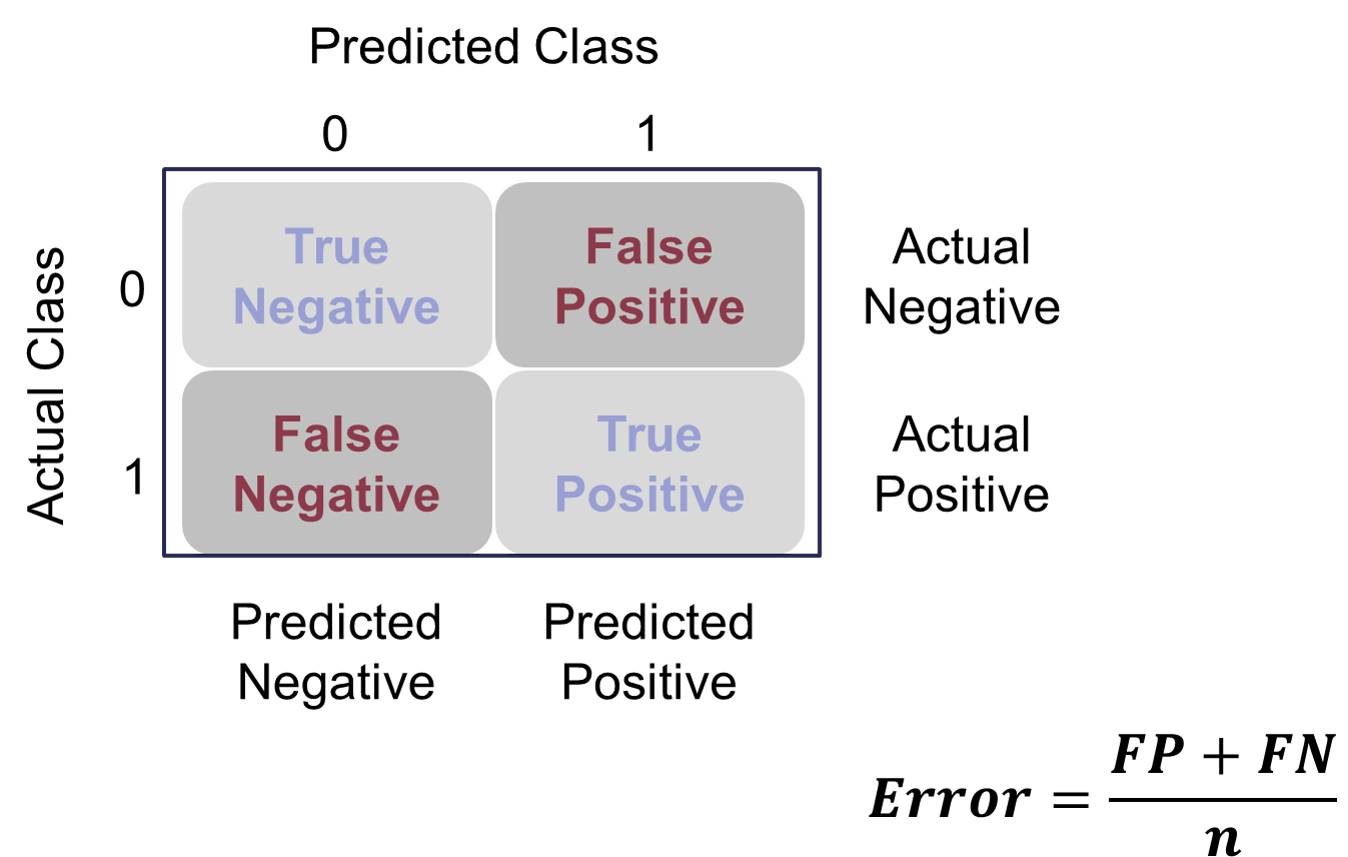{fig-align="center" width="6in"}However, caution should be used with these metrics as they can easily be fooled if *only* focusing on them. If your data has 10% events and 90% non-events, you can easily have a 90% accurate model by guessing non-events for every observation. Instead, having less accuracy might be better if we can predict both events and non-events. These numbers are still great to report! They are just not the best to decide which model is best.Let's see how to do this in each of our softwares!::: {.panel-tabset .nav-pills}## RR produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities.We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a `for` loop in R. However, the `measureit` function can do this for us. The inputs for this function are the predicted probabilities first, followed by the target variable. The `measure` option allows you to define additional measures to calculate at each cut-off. In the code below we ask for accuracy (`ACC`) and F1-score (`FSCR`). From there we combine these variables into a single dataframe and print the observations with the `print` function.```{r}logit_meas <-measureit(train$p_hat, train$Bonus, measure =c("ACC", "FSCR"))summary(logit_meas)acc_table <-data.frame(Cutoff = logit_meas$Cutoff, Acc = logit_meas$ACC)head(arrange(acc_table, desc(Acc)), n =10)```From the output we can see the accuracy is maximized at 86.69%. The predicted probability that this occurs at (the optimal cut-off) is defined as 0.531. In other words, if our model predicts a probability above 0.531 then we should call this an event. Any predicted probability below 0.531 should be called a non-event, according to the accuracy metric.There is more to model building than simply maximizing overall classification accuracy. These are good numbers to report, but not necessarily to choose models on.## PythonPython produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities.We want to look at all classification tables for all values of cut-offs between 0 and 1. We can easily loop through this calculation with a `for` loop in Python using the `accuracy_score` function. The input for the function are the target variable first, followed by the predicted probabilities. We loop through many cut-off values to find the optimal accuracy.```{python}from sklearn.metrics import accuracy_scoreaccuracy = np.array([])for y inrange(100): train['pred'] = train['p_hat'].map(lambda x: 1if x > y/100else0) value_a = accuracy_score(train['Bonus'], train['pred']) accuracy = np.append(accuracy, value_a)data = {'Accuracy': accuracy, 'Cut-off': range(100)}acc_s = pd.DataFrame(data)acc_s.sort_values(by = ['Accuracy'], ascending =False)```From the output we can see the accuracy is maximized at 86.64%. The predicted probability that this occurs at (the optimal cut-off) is defined as 0.53. In other words, if our model predicts a probability above 0.53 then we should call this an event. Any predicted probability below 0.53 should be called a non-event, according to the accuracy metric.There is more to model building than simply maximizing overall classification accuracy. These are good numbers to report, but not necessarily to choose models on.## SASPROC LOGISTIC produces classification tables for any cut-off that you determine. Remember that a cut-off is simply the point where you decide to predict an event and non-event from your predicted probabilities. The `ctable` option in the MODEL statement creates the classification table for us. The `pprob` option defines the cut-off (or range of cut-offs) for this classification table. We want to look at all classification tables for cut-offs ranging from a predicted probability of 0 to 0.98 by steps of 0.02. From there we use PROC SORT to rank these by the *Correct* variable produced in PROC LOGISTIC and print the first 10 observations with PROC PRINT.```{r}#| eval: falseods html select Classification;proc logistic data=logistic.ames_train plots(only)=(oddsratio); class House_Style Full_Bath Half_Bath Central_Air / param=ref; model Bonus(event='1') = Gr_Liv_Area House_Style Garage_Area Fireplaces Full_Bath Lot_Area Central_Air TotRms_AbvGrd Gr_Liv_Area|Fireplaces @2/ ctable pprob =0 to 0.98 by 0.02; ods output classification=classtable; title 'Modeling Bonus Eligibility';run;quit;proc sort data=classtable; by descending Correct;run;proc print data=classtable (obs =10);run;```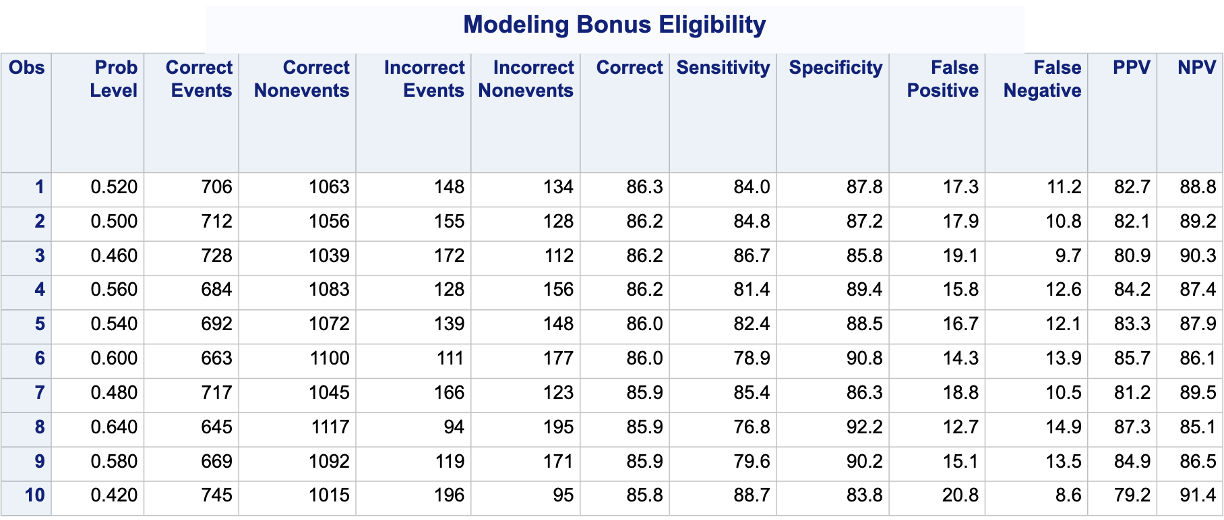{fig-align="center" width="6in"}From the output we can see the accuracy is maximized at 86.3%. The predicted probability that this occurs at (the optimal cut-off) is defined at 0.52. In other words, if our model predicts a probability above 0.52 then we should call this an event. Any predicted probability below 0.52 should be called a non-event, according to the accuracy metric.There is more to model building than simply maximizing overall classification accuracy. These are good numbers to report, but not necessarily to choose models on.:::# Optimal Cut-offClassification is a decision that is extraneous to statistical modeling. Although logistic regressions tend to work well in classification, it is a probability model and does not output events and non-events.Classification assumes cost for each observation is the same, which is rarely true. It is always better to consider the costs of false positives and false negatives when considering cut-offs in classification. The previous sections talk about many ways to determine "optimal" cut-offs when costs are either not known or not necessary. However, if costs are known, they should drive the cut-off decision rather than modeling metrics that do not account for cost.