These notes will primary focus on binary logistic regression. It is the most common type of logistic regression, and sets up the foundation for both ordinal and nominal logistic regression.
The linear probability model is not as widely used since probabilities do not tend to follow the properties of linearity in relation to their predictors. Also, the linear probability model possibly produces predictions outside of the bounds of 0 and 1 (where probabilities should be!). For completeness sake however, here is the linear probability model:
Linear Probability Model
Let’s first view what a linear probability model would look like plotted on our data and then we can build the model.
lp.model <-lm(Bonus ~ Gr_Liv_Area, data = train)with(train, plot(x = Gr_Liv_Area, y = Bonus,main ='OLS Regression?',xlab ='Greater Living Area (Sqft)',ylab ='Bonus Eligibility'))abline(lp.model)
Even though it doesn’t appear to really look like our data, let’s fit this linear probability model anyway for completeness sake.
Code
lp.model <-lm(Bonus ~ Gr_Liv_Area, data = train)summary(lp.model)
Call:
lm(formula = Bonus ~ Gr_Liv_Area, data = train)
Residuals:
Min 1Q Median 3Q Max
-2.70766 -0.29160 -0.09983 0.39432 0.86198
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.149e-01 2.776e-02 -14.94 <2e-16 ***
Gr_Liv_Area 5.534e-04 1.765e-05 31.36 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4044 on 2049 degrees of freedom
Multiple R-squared: 0.3243, Adjusted R-squared: 0.324
F-statistic: 983.6 on 1 and 2049 DF, p-value: < 2.2e-16
Code
qqnorm(rstandard(lp.model),ylab ="Standardized Residuals",xlab ="Normal Scores",main ="QQ-Plot of Residuals")qqline(rstandard(lp.model))
Code
plot(predict(lp.model), resid(lp.model), ylab="Residuals", xlab="Predicted Values", main="Residuals of Linear Probability Model") abline(0, 0)
As we can see from the charts above, the assumptions of ordinary least squares don’t really hold in this situation. Therefore, we should be careful interpreting the results of the model. Maybe a better model won’t have these problems?
Code
from matplotlib import pyplot as pltimport seaborn as snssns.lmplot(data = train, x ='Gr_Liv_Area', y ='Bonus', scatter =True)
Code
plt.show()
Even though it doesn’t appear to really look like our data, let’s fit this linear probability model anyway for completeness sake.
Code
import statsmodels.formula.api as smflp_model = smf.ols("Bonus ~ Gr_Liv_Area", data = train).fit()lp_model.summary()
OLS Regression Results
Dep. Variable:
Bonus
R-squared:
0.324
Model:
OLS
Adj. R-squared:
0.324
Method:
Least Squares
F-statistic:
983.6
Date:
Mon, 24 Jun 2024
Prob (F-statistic):
1.11e-176
Time:
19:32:33
Log-Likelihood:
-1052.4
No. Observations:
2051
AIC:
2109.
Df Residuals:
2049
BIC:
2120.
Df Model:
1
Covariance Type:
nonrobust
coef
std err
t
P>|t|
[0.025
0.975]
Intercept
-0.4149
0.028
-14.944
0.000
-0.469
-0.360
Gr_Liv_Area
0.0006
1.76e-05
31.362
0.000
0.001
0.001
Omnibus:
1.621
Durbin-Watson:
2.012
Prob(Omnibus):
0.445
Jarque-Bera (JB):
1.587
Skew:
0.068
Prob(JB):
0.452
Kurtosis:
3.013
Cond. No.
4.89e+03
Notes: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. [2] The condition number is large, 4.89e+03. This might indicate that there are strong multicollinearity or other numerical problems.
Code
import statsmodels.api as smasma.qqplot(lp_model.resid)plt.show()
As we can see from the charts above, the assumptions of ordinary least squares don’t really hold in this situation. Therefore, we should be careful interpreting the results of the model. Maybe a better model won’t have these problems?
Code
proc sgplot data=logistic.ames_train; reg x = Gr_Liv_Area y = Bonus; title 'OLS for Binary Response?'; xaxis label='Greater Living Area (Sqft)'; yaxis label='Bonus Eligible';run;
Even though it doesn’t appear to really look like our data, let’s fit this linear probability model anyway for completeness sake.
Code
proc reg data=logistic.ames_train plot(unpack)=diagnostics; model Bonus = Gr_Liv_Area;run;quit;
As we can see from the charts above, the assumptions of ordinary least squares don’t really hold in this situation. Therefore, we should be careful interpreting the results of the model. Maybe a better model won’t have these problems?
Binary Logistic Regression Model
Due to the limitations of the linear probability model, people typically just use the binary logistic regression model. The logistic regression model does not have the limitations of the linear probability model. The outcome of the logistic regression model is the probability of getting a 1 in a binary variable, \(E(y_i) = P(y_i = 1) = p_i\). That probability is calculated as follows:
This function has the desired properties for predicting probabilities. The predicted probability from the above equation will always be between 0 and 1. The parameter estimates do not enter the function linearly (this is a non-linear regression model), and the rate of change of the probability varies as the predictor variables vary as seen below.
Logistic Curve
To create a linear model, a link function is applied to the probabilities. The specific link function for logistic regression is called the logit function.
The relationship between the predictor variables and the logits are linear in nature as the logits themselves are unbounded. This structure looks much more like our linear regression model structure. However, logistic regression does not use ordinary least squares (OLS) to estimate the coefficients in our model. OLS requires residuals which the logistic regression model does not provide. The target variable is binary in nature, but the predictions are probabilities. Therefore, we cannot calculate a traditional residual. Instead, logistic regression uses maximum likelihood estimation.
Maximum likelihood estimation (MLE) is a very popular technique for estimating statistical models. It uses the assumed distribution (here logistic) to find the “most likely” values of the parameters to produce the data we see. In fact, it can be shown mathematically that the OLS solution in linear regression is the same as the MLE for linear regression. The likelihood function measures how probable a specific grid of \(\beta\) values is to have produced your data, so we want to MAXIMIZE that as seen in the plot below.
Maximum Likelihood Function Example
Let’s see how to run binary logistic regression in each of our softwares!
The glm function in R will provide us the ability to model binary logistic regressions. Similar to the lm function, you can specify a model formula. Notice the factor function on the Central_Air variable. This will convert this categorical variable into usable design variables for the modeling function.
The family = binomial(link = "logit") option is there to specify that we are building a logistic model. Generalized linear models (GLM) are a general class of models where logistic regression is a special case where the link function is the logit function. Use the summary function to look at the necessary output.
Code
logit.model <-glm(Bonus ~ Gr_Liv_Area +factor(Central_Air), data = train, family =binomial(link ="logit"))summary(logit.model)
Call:
glm(formula = Bonus ~ Gr_Liv_Area + factor(Central_Air), family = binomial(link = "logit"),
data = train)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.035e+01 6.422e-01 -16.12 < 2e-16 ***
Gr_Liv_Area 4.112e-03 1.962e-04 20.96 < 2e-16 ***
factor(Central_Air)Y 3.952e+00 5.180e-01 7.63 2.35e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2775.8 on 2050 degrees of freedom
Residual deviance: 1808.8 on 2048 degrees of freedom
AIC: 1814.8
Number of Fisher Scoring iterations: 6
Let’s examine the output above. Scanning down the output, you can see the actual logistic regression equation itself for each of the variables, including the design variable created for Central_Air with the factor function. At our significance level (we used an 0.005 significance level for this analysis based on the sample size) it appears that both of these variables are significant. We will address variable selection in the “Subset Selection and Diagnostics” section.
To perform a global Likelihood Ratio Test to see if any of the variables are significant overall you can run the following code.
Code
logit.model.r <-glm(Bonus ~1, data = train, family =binomial(link ="logit"))anova(logit.model, logit.model.r, test ='LRT')
The above code creates a second model without any variables. It then performs a Likelihood Ratio Test (LRT) on this model compared to the original model. The results of this test show the usefulness of all the variables. This is comparable to the global F-test in linear regression. The two models are significantly different (based on our significance level) which implies that at least one of the variables is significant. If these models weren’t significantly different then the variables would be adding no value statistically.
For the Central_Air variable, we only have one design variable, but if our variable had 3 or more categories, we would have multiple design variables. Categorical variables should not be evaluated solely based on their individual categorical design variable significance as those represent specific tests between combinations of categories. The variable overall must be evaluated for its usefulness to the model. We will produce that with the next piece of code below to check the Fireplaces variable.
Code
logit.model.f <-glm(Bonus ~ Gr_Liv_Area +factor(Central_Air) +factor(Fireplaces), data = train, family =binomial(link ="logit"))car::Anova(logit.model.f, test ='LR', type ='III')
The above code creates a second model with the Fireplaces categorical variable. It then uses a different Anova function from the car package (notice the capital A in Anova). This function performs a LRT comparing a model with and without a variable but leaving every other variable in there. Notice the options for test = 'LR' to get the LRT as well as the type = 'III' to get the Type 3 LRTs. This just means that the test only drops that specific variable when comparing to the full model. The results of this test show the usefulness of the Fireplaces variable. The two models are significantly different (based on our significance level) which implies that the Fireplaces variable (the only difference between comparing a model with and without the Fireplaces variable) is significant as a whole. If these models weren’t significantly different then the Fireplaces variable would be adding no value statistically.
Lastly we can get the odds ratios for each of the above mentioned variables with the following code:
Odds ratios are a great way of interpreting the output from a logistic regression. For example, let’s look at the Central_Air variable odds ratio. This tells us that homes with central air are 52 times as likely (in terms of odds) of being bonus eligible, on average, then homes without central air. To practice interpreting continuous variables, let’s look at the Gr_Liv_Area variable. Every additional square foot of living area leads to the home being 1.004 times as likely to be bonus eligible. This maybe a little harder to easily understand. Another way to put this would be that every additional square foot of living area increases the odds of the home being bonus eligible by 0.4% (100*(1.004 - 1)) on average.
The GLM.from_formula function and the fit attribute in Python from the statsmodels.genmod.generalized_linear_model package will provide us the ability to model binary logistic regressions. With this function you can specify a model formula, similar to R. Notice the C function on the Central_Air variable. This will convert this categorical variable into usable design variables for the modeling function.
The family = Binomial() option is there to specify that we are building a logistic model. Generalized linear models (GLM) are a general class of models where logistic regression is a special case where the link function is the logit function. Use the summary function to look at the necessary output.
Code
from statsmodels.genmod.families import Binomialfrom statsmodels.genmod.generalized_linear_model import GLMlog_model = GLM.from_formula('Bonus ~ Gr_Liv_Area + C(Central_Air)', data = train, family = Binomial()).fit()log_model.summary()
Generalized Linear Model Regression Results
Dep. Variable:
Bonus
No. Observations:
2051
Model:
GLM
Df Residuals:
2048
Model Family:
Binomial
Df Model:
2
Link Function:
Logit
Scale:
1.0000
Method:
IRLS
Log-Likelihood:
-904.42
Date:
Mon, 24 Jun 2024
Deviance:
1808.8
Time:
19:32:34
Pearson chi2:
1.98e+07
No. Iterations:
7
Pseudo R-squ. (CS):
0.3759
Covariance Type:
nonrobust
coef
std err
z
P>|z|
[0.025
0.975]
Intercept
-10.3546
0.642
-16.124
0.000
-11.613
-9.096
C(Central_Air)[T.Y]
3.9519
0.518
7.629
0.000
2.937
4.967
Gr_Liv_Area
0.0041
0.000
20.959
0.000
0.004
0.004
Let’s examine the output above. Scanning down the output, you can see the actual logistic regression equation itself for each of the variables, including the design variable created for Central_Air with the factor function. At our significance level (we used an 0.005 significance level for this analysis based on the sample size) it appears that both of these variables are significant. We will address variable selection in the “Subset Selection and Diagnostics” section.
Python also provides the Global Likelihood Ratio Test (‘LLR p-value’ in the output). The results of this test show the usefulness of all the variables. This is comparable to the global F-test in linear regression. The two models are significantly different (based on our significance level of 0.005) which implies that at least one of the variables is significant. If these models weren’t significantly different then the variables would be adding no value statistically.
For the Central_Air variable, we only have one design variable, but if our variable had 3 or more categories, we would have multiple design variables. Categorical variables should not be evaluated solely based on their individual categorical design variable significance as those represent specific tests between combinations of categories. The variable overall must be evaluated for its usefulness to the model. We will produce that with the next piece of code below to check the Fireplaces variable.
Warning: Maximum number of iterations has been exceeded.
Current function value: 0.425703
Iterations: 35
/Users/aric/Library/r-miniconda-arm64/envs/r-reticulate/lib/python3.9/site-packages/statsmodels/base/model.py:607: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
warnings.warn("Maximum Likelihood optimization failed to "
Now we have the likelihood values from the original model without fireplace using the llf attribute from the log_model object and the likelihood values from a model with the addition of the Fireplaces variable. From there we can calculate the LRT by hand using the code below.
Code
import scipy as spLR_statistic =-2*(reduced_ll-full_ll)print(LR_statistic)
The above code performs a LRT comparing a model with and without a variable but leaving every other variable in there. Notice the 4 degrees of freedom in the sp.stats.chi2.sf function. This is because of the 5 values for the Fireplaces variable. The degrees of freedom is the difference in number of \(\beta\) coefficients between the two models. If Fireplaces has 5 levels, then we only need 4 variables in our regression. The results of this test show the usefulness of the Fireplaces variable. The two models are significantly different (based on our significance level) which implies that the Fireplaces variable (the only difference between comparing a model with and without the Fireplaces variable) is significant as a whole. If these models weren’t significantly different then the Fireplaces variable would be adding no value statistically.
Lastly we can get the odds ratios for each of the above mentioned variables with the following code:
Odds ratios are a great way of interpreting the output from a logistic regression. For example, let’s look at the Central_Air variable odds ratio. This tells us that homes with central air are 52 times as likely (in terms of odds) of being bonus eligible, on average, then homes without central air. To practice interpreting continuous variables, let’s look at the Gr_Liv_Area variable. Every additional square foot of living area leads to the home being 1.004 times as likely to be bonus eligible. This maybe a little harder to easily understand. Another way to put this would be that every additional square foot of living area increases the odds of the home being bonus eligible by 0.4% (100*(1.004 - 1)) on average.
PROC LOGISTIC has a built in CLASS statement. This allows us to input categorical variables easily into our logistic regression. The Central_Air variable had 2 categories - Y and N. We will use the N as our reference category as you can see with the ref = option listed after the Central_Air variable. By default, SAS uses effects coding for all categorical variables. To switch to reference coding we use the param = ref option at the end of the CLASS statement.
For our odds ratios as well as parameter estimates, the profile likelihood estimation method is preferred to the Wald approximation. This is accomplished by using the clodds = pl and clparm = pl options.
Code
proc logistic data=logistic.ames_train plots(only)=(oddsratio); class Central_Air(ref='N') / param=ref; model Bonus(event='1') = Gr_Liv_Area Central_Air / clodds=pl clparm=pl; title 'Modeling Bonus Eligibility';run;quit;
Let’s examine the output above. Scanning down the output, you can see that SAS provided us with a summary of the number of observations read and used in the analysis as well as a frequency breakdown of the target variable.
The important piece of the output here is the model convergence status. Note that the model converged. This estimation is done through maximum likelihood estimation (MLE) so we need this convergence. We will address what happens when this doesn’t converge in the “Data Considerations” section.
SAS then provides some basic model metrics like the AIC and SC as well as the Global Likelihood Ratio Test. The small p-value here (we used an 0.005 significance level for this analysis based on the sample size) implies that at least one of the variables is useful in the prediction of bonus eligibility. The Type 3 Analysis table provides us with a variable by variable breakdown to see which of the variables prove helpful. At our significance level it appears that the variables are both significant. We will address variable selection in the “Subset Selection and Diagnostics” section.
The MLE table provides us with the actual logistic regression equation itself for each of the variables, including the design variables created for Central_Air with the CLASS statement.
The Association of Predicted Probabilities table provides us with many model metrics that we will discuss in the “Model Assessment” section.
Lastly we are provided with the odds ratios for each of the above mentioned variables. Odds ratios are a great way of interpreting the output from a logistic regression. For example, let’s look at the Central_Air variable odds ratio. This tells us that homes with central air are 52 times as likely (in terms of odds) of being bonus eligible, on average, then homes without central air. To practice interpreting continuous variables, let’s look at the Gr_Liv_Area variable. Every additional square foot of living area leads to the home being 1.004 times more likely to be bonus eligible. This maybe a little harder to easily understand. Another way to put this would be that every additional square foot of living area increases the odds of the home being bonus eligible by 0.4% (100*(1.004 - 1)) on average.
Testing Assumptions
Outside of independence of observations, the biggest assumption of logistic regression is that the continuous predictor variables are linearly related to the logit function (our transformation of the probability of our target). A great way to check this assumption is through Generalized Additive Models (GAMs).
Generalized additive models (GAM’s) can be used to help evaluate the linearity of the relationship between the continuous predictor variables and the logit. When GAM’s are applied to a logistic regression, the following is the new model:
\[
\log(\frac{p_i}{1-p_i}) = \beta_0 + f_1(x_1) + \cdots + f_k(x_k)
\] These functions applied to the continuous predictor variables need to be estimated. GAM’s use spline functions to estimate these. If these splines say a straight line is good, then the assumption is met. There are some options if the assumption is not met:
Use the GAM representation of the logistic regression model instead of the traditional logistic regression model.
Strategically bin the continuous predictor variable.
In the first approach, instead of using the logistic regression model as previously defined, the logistic GAM would be used for predictions. The GAM version of the logistic regression is less interpretable in the traditional sense of odds ratios. Instead, plots are used to show potentially complicated relationships.
In the second approach, the continuous variables are categorized and put in the original logistic framework in their categorical form. There are statistical approaches to doing this, but one could also use the GAM plots to decide on possible splits for binning the data.
Let’s see how to produce GAMs in each of our softwares!
For GAMs we can use the gam function in R. Similar to the glm function, you have a model formula to specify the full model. Categorical variables can still be handled with the factor function. The only difference is that we will test the continuous variables with splines to see if those splines produce anything significantly better than their linear representations. The s function is put on every one of the continuous variables. The family = and link = options are used to specify the logistic regression. The method = option is specified here as their are multiple approaches to fitting the GAM in R. We will use the REML approach.
From the above output we can see that Gr_Liv_Area and Central_Air are both still significant in this model. However, now the Gr_Liv_Area variable is a more complicated transformation. As seen in the graph above, it appears that Gr_Liv_Area has a nonlinear pattern with the logit. In fact, the edf (or estimated degrees of freedom) in the output above also shows us this. If the edf value was 1, the best spline was a linear relationship with the target (linearity assumption holds). However, since it is not equal to 1, we cannot say this. How close is close enough to 1? If you wanted a statistical test, we could compare a model with a linear representation of Gr_Liv_Area to the spline version with a Likelihood Ratio test.
The null hypothesis to the above test is that the two models are equal. This null hypothesis would imply that the linearity assumption would hold since the spline is not estimating anything more complicated. However, the p-value was extremely small and therefore the two models are not equal to other. This means that Gr_Liv_Area cannot just be modeled linearly with the logit.
From the plot above, it appears that Gr_Liv_Area has three main patterns - below 1300 sqft, between 1300 and 4000 sqft, and above 4000 sqft. But we want bins that are about the same in their effect. Let’s create a new variable along the cut points of < 1000, 1000-1500, 1500-3000, 300-4500, 4500+.
Now let’s rebuild the logistic regression model with this new categorical version of the Gr_Liv_Area variable.
Code
logit.model.bin <-glm(Bonus ~factor(Gr_Liv_Area_BIN) +factor(Central_Air),data = train, family =binomial(link ='logit'))summary(logit.model.bin)
Call:
glm(formula = Bonus ~ factor(Gr_Liv_Area_BIN) + factor(Central_Air),
family = binomial(link = "logit"), data = train)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -8.8210 1.1065 -7.972 1.56e-15 ***
factor(Gr_Liv_Area_BIN)(1e+03,1.5e+03] 4.5121 1.0052 4.489 7.16e-06 ***
factor(Gr_Liv_Area_BIN)(1.5e+03,3e+03] 6.6437 1.0049 6.611 3.81e-11 ***
factor(Gr_Liv_Area_BIN)(3e+03,4.5e+03] 21.1646 363.8508 0.058 0.95361
factor(Gr_Liv_Area_BIN)(4.5e+03, Inf] 5.5986 1.7331 3.230 0.00124 **
factor(Central_Air)Y 3.2224 0.4734 6.807 9.95e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2775.8 on 2050 degrees of freedom
Residual deviance: 1892.0 on 2045 degrees of freedom
AIC: 1904
Number of Fisher Scoring iterations: 14
From the above output, we can see that Gr_Liv_Area_BIN is still a significant variable in our model. The nice part about using a categorical representation for the variable instead of using the GAM for predictions is that we still have some interpretability on this variable using odds ratios for the categories.
For GAMs we can use the GLMGam.from_formula function in Python. Similar to the GLM.from_formula function, you have a model formula to specify the full model. Categorical variables can still be handled with the C function. The only difference is that we will test the continuous variables with splines to see if those splines produce anything significantly better than their linear representations. The BSplines function is put on every one of the continuous variables and then added into the smoother option in the GLMGam function. The family = option is used to specify the logistic regression.
Code
import statsmodels as smfrom statsmodels.gam.api import GLMGam, BSplinesx_spline = train['Gr_Liv_Area']bs = BSplines(x_spline, df =5, degree =3)gam_model = GLMGam.from_formula('Bonus ~ C(Central_Air)', data = train, smoother = bs, family = sm.api.families.Binomial()).fit()gam_model.summary()
Generalized Linear Model Regression Results
Dep. Variable:
Bonus
No. Observations:
2051
Model:
GLMGam
Df Residuals:
2045.00
Model Family:
Binomial
Df Model:
5.00
Link Function:
Logit
Scale:
1.0000
Method:
PIRLS
Log-Likelihood:
-846.65
Date:
Mon, 24 Jun 2024
Deviance:
1693.3
Time:
19:32:36
Pearson chi2:
1.89e+03
No. Iterations:
10
Pseudo R-squ. (CS):
0.4101
Covariance Type:
nonrobust
coef
std err
z
P>|z|
[0.025
0.975]
Intercept
-58.7286
11.955
-4.913
0.000
-82.160
-35.298
C(Central_Air)[T.Y]
3.5444
0.492
7.207
0.000
2.581
4.508
Gr_Liv_Area_s0
52.1509
12.337
4.227
0.000
27.970
76.332
Gr_Liv_Area_s1
59.8710
11.259
5.318
0.000
37.803
81.938
Gr_Liv_Area_s2
60.0950
13.303
4.517
0.000
34.022
86.168
Gr_Liv_Area_s3
54.0120
11.879
4.547
0.000
30.730
77.294
Code
gam_model.plot_partial(smooth_index =0)plt.show()
From the above output we can see that Gr_Liv_Area and Central_Air are both still significant in this model. However, now the Gr_Liv_Area variable is a more complicated transformation. As seen in the graph above, it appears that Gr_Liv_Area has a nonlinear pattern with the logit. If you wanted a statistical test, we could compare a model with a linear representation of Gr_Liv_Area to the spline version with a Likelihood Ratio test to see if any value is added from the spline.
The null hypothesis to the above test is that the two models are equal. This null hypothesis would imply that the linearity assumption would hold since the spline is not estimating anything more complicated. However, the p-value was extremely small and therefore the two models are not equal to other. This means that Gr_Liv_Area cannot just be modeled linearly with the logit.
From the plot above, it appears that Gr_Liv_Area has three main patterns - below 1300 sqft, between 1300 and 4000 sqft, and above 4000 sqft. But we want bins that are about the same in their effect. Let’s create a new variable along the cut points of < 1000, 1000-1500, 1500-3000, 300-4500, 4500+ with the cut function.
Now let’s rebuild the logistic regression model with this new categorical version of the Gr_Liv_Area variable.
Code
log_model_bin = smf.logit("Bonus ~ C(Gr_Liv_Area_BIN) + C(Central_Air)", data = train).fit()
Warning: Maximum number of iterations has been exceeded.
Current function value: 0.461249
Iterations: 35
/Users/aric/Library/r-miniconda-arm64/envs/r-reticulate/lib/python3.9/site-packages/statsmodels/base/model.py:607: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
warnings.warn("Maximum Likelihood optimization failed to "
From the above output, we can see that Gr_Liv_Area_BIN is still a significant variable in our model. The nice part about using a categorical representation for the variable instead of using the GAM for predictions is that we still have some interpretability on this variable using odds ratios for the categories.
For GAMs we can use PROC GAM. Similar to PROC LOGISTIC, we fit our MODEL statement with our full model. PROC GAM even has a CLASS statement for categorical variables. The only difference is that we will test the continuous variables with splines to see if those splines produce anything significantly better than their linear representations. The spline option is put on every one of the continuous variables. We want to leave the categorical variables alone so use the param option on those. The dist = and link = options are used to specify the logistic regression.
The ods statement here selects only the significance of the splines (ANODEV option) and the component plots (SmoothingComponentPlot option) since that is all we desire to test the assumption.
Code
ods html select ANODEV SmoothingComponentPlot;proc gam data=logistic.ames_train plots =components(clm commonaxes); class Central_Air(ref='N') / param = ref; model Bonus(event='1') =spline(Gr_Liv_Area, df =2) param(Central_Air) / dist = binomial link = logit;run;quit;
Here we can see that the relationship with Gr_Liv_Area is more complicated than just linear in terms of its relationship with the logit. If we saw a straight line here we would be able to conclude the linearity assumption held.
From the plot above, it appears that Gr_Liv_Area has three main patterns - below 1300 sqrt, between 1300 and 4000 sqft, and above 4000 sqft. But we want bins that are about the same in their effect. Let’s create a new variable along the cut points of < 1000, 1000-1500, 1500-3000, 300-4500, 4500+.
Code
proc format;value Gr_Liv_AreaFMT low -<1000="Small"1000-<1500="Small-Medium"1500-<3000="Medium"3000-<4500="Medium-Large"4500- high ="Large";run;proc logistic data=logistic.ames_train plots(only)=(oddsratio); format Gr_Liv_Area Gr_Liv_AreaFMT.; class Central_Air(ref='N') Gr_Liv_Area / param=ref; model Bonus(event='1') = Gr_Liv_Area Central_Air / clodds=pl clparm=pl; title 'Modeling Bonus Eligibility';run;quit;
From the above output, we can see that the binned version of Gr_Liv_Area is still a significant variable in our model. The nice part about using a categorical representation for the variable instead of using the GAM for predictions is that we still have some interpretability on this variable using odds ratios for the categories.
Predicted Values
Obviously, the predicted logit values really don’t help us too much. Instead we want to gather the predicted probabilities of the target variable categories. Luckily, the software we are looking at make this rather easy to do.
Let’s see how to produce these predicted probabilities in each of our softwares!
If you split your data into training and validation (and/or testing) you could score that data set using the predict function. Here we are creating a new data set of 5 observations to score instead. The predict function has three primary pieces - the model object (here called logit.model, the newdata = option, and the type = option. The newdata = option is where you specify the data set you want scored, while the type = option specifies the type of prediction you want. Here we want the response option since we are predicting the probabilities. If we wanted the predicted logit values we could use the option terms instead.
The visreg function below creates the effect plot, which will show us the logistic curve across different values of the continuous variable, here Gr_Liv_Area. It will show each of the categorical variable categories as a separate curve. If there is were more continuous variables they are just taken at a specified value - their average value.
Code
new_ames <-data.frame(Gr_Liv_Area =c(1500, 2000, 2250, 2500, 3500),Central_Air =c("N", "Y", "Y", "N", "Y"))new_ames <-data.frame(new_ames, 'Pred'=predict(logit.model, newdata = new_ames, type ="response"))library(visreg)visreg(logit.model, "Gr_Liv_Area", by ="Central_Air", scale ="response",overlay =TRUE,xlab ='Greater Living Area (Sqft)',ylab ='Bonus Eligibility')
Code
print(new_ames)
Gr_Liv_Area Central_Air Pred
1 1500 N 0.01498152
2 2000 Y 0.86084436
3 2250 Y 0.94534188
4 2500 N 0.48167577
5 3500 Y 0.99966165
The print function above looks at the scored data set. Notice that we added an additional column to our original data set we were scoring. This is the predicted probability of a 1. This is default in R. If you want the predicted probability of the 0 category, you can just subtract this prediction from 1.
If you split your data into training and validation (and/or testing) you could score that data set using the predict function. Here we are creating a new data set of 5 observations to score instead. The predict function on the model object (here called log_model) just needs the dataset to be scored (here called new_ames). By default, the predict function gives the predicted probabilities.
Gr_Liv_Area Central_Air Pred
0 1500 N 0.014982
1 2000 Y 0.860844
2 2250 Y 0.945342
3 2500 N 0.481676
4 3500 Y 0.999662
The print function above looks at the scored data set. Notice that we added an additional column to our original data set we were scoring. This is the predicted probability of a 1. This is default in Python. If you want the predicted probability of the 0 category, you can just subtract this prediction from 1.
The regplot function below creates the effect plot, which will show us the logistic curve across different values of the continuous variable, here Gr_Liv_Area. We overlay two of these curves, one for each of the categories of Central_Air. If there is were more continuous variables they are just taken at a specified value - their average value.
Code
plt.cla()fig, ax = plt.subplots()sns.regplot(data = train[train['Central_Air'] =='Y'], x ='Gr_Liv_Area', y ='Bonus', scatter =True, logistic =True, ax = ax)sns.regplot(data = train[train['Central_Air'] =='N'], x ='Gr_Liv_Area', y ='Bonus', scatter =True, logistic =True, ax = ax)plt.show()
If you split your data into training and validation (and/or testing) you could score that data set using PROC LOGISTIC’s built in SCORE statement. Here we are creating a new data set of 5 observations to score instead. The SCORE statement has two primary pieces - data = and out =. The data = piece is where you specify the data set you want scored, while the out = piece is the name of the new scored data set.
The ods statement below only selects the effect plot, which will show us the logistic curve across different values of the first continuous variable, here Gr_Liv_Area. It will show each of the categorical variable categories as a separate curve. The other continuous variables are just taken at their average value.
Code
data new_ames; input Gr_Liv_Area Central_Air $; datalines;1500 N2000 Y2250 Y2500 N3500 Y ;run;ods html select EFFECTPLOT;proc logistic data=logistic.ames_train plots(only)=(oddsratio effect); class Central_Air(ref='N') / param=ref; model Bonus(event='1') = Gr_Liv_Area Central_Air / clodds=pl clparm=pl; title 'Modeling Bonus Eligibility'; score data=new_ames out=ames_scored;run;quit;proc print data=ames_scored;run;
The PROC PRINT above looks at the scored data set. Notice that there are four additional columns that we have on our original data set we were scoring. The first two, F_Bonus and I_Bonus, represent the original target variable and the predicted target variable respectively. Specifically, they stand for FROM and INTO. SAS decides the predicted category rather crudely by assuming if the predicted probability of the category is above 0.5, then it predicts that category will occur. We will see in the “Model Assessment” section that 0.5 is rarely the optimal cut-off.
The final two categories are the predicted probabilities for each of the values of the target variable - P_0 and P_1. These are just the predicted probability of 0 and 1 in our target variable respectively.
---title: "Binary Logistic Regression"format: html: code-fold: show code-tools: trueeditor: visual---```{r}#| include: false#| warning: falselibrary(AmesHousing)ames <-make_ordinal_ames()library(tidyverse)ames <- ames %>%mutate(Bonus =ifelse(Sale_Price >175000, 1, 0))set.seed(123)ames <- ames %>%mutate(id =row_number())train <- ames %>%sample_frac(0.7)test <-anti_join(ames, train, by ='id')``````{python}#| include: falsetrain = r.traintest = r.test```# IntroductionThese notes will primary focus on binary logistic regression. It is the most common type of logistic regression, and sets up the foundation for both ordinal and nominal logistic regression.The linear probability model is not as widely used since probabilities do not tend to follow the properties of linearity in relation to their predictors. Also, the linear probability model possibly produces predictions outside of the bounds of 0 and 1 (where probabilities should be!). For completeness sake however, here is the linear probability model:# Linear Probability ModelLet's first view what a linear probability model would look like plotted on our data and then we can build the model.::: {.panel-tabset .nav-pills}## R```{r}lp.model <-lm(Bonus ~ Gr_Liv_Area, data = train)with(train, plot(x = Gr_Liv_Area, y = Bonus,main ='OLS Regression?',xlab ='Greater Living Area (Sqft)',ylab ='Bonus Eligibility'))abline(lp.model)```Even though it doesn't appear to really look like our data, let's fit this linear probability model anyway for completeness sake.```{r}lp.model <-lm(Bonus ~ Gr_Liv_Area, data = train)summary(lp.model)qqnorm(rstandard(lp.model),ylab ="Standardized Residuals",xlab ="Normal Scores",main ="QQ-Plot of Residuals")qqline(rstandard(lp.model))plot(predict(lp.model), resid(lp.model), ylab="Residuals", xlab="Predicted Values", main="Residuals of Linear Probability Model") abline(0, 0) ```As we can see from the charts above, the assumptions of ordinary least squares don't really hold in this situation. Therefore, we should be careful interpreting the results of the model. Maybe a better model won't have these problems?## Python```{python}from matplotlib import pyplot as pltimport seaborn as snssns.lmplot(data = train, x ='Gr_Liv_Area', y ='Bonus', scatter =True)plt.show()```Even though it doesn't appear to really look like our data, let's fit this linear probability model anyway for completeness sake.```{python}import statsmodels.formula.api as smflp_model = smf.ols("Bonus ~ Gr_Liv_Area", data = train).fit()lp_model.summary()``````{python}import statsmodels.api as smasma.qqplot(lp_model.resid)plt.show()```As we can see from the charts above, the assumptions of ordinary least squares don't really hold in this situation. Therefore, we should be careful interpreting the results of the model. Maybe a better model won't have these problems?## SAS```{r}#| eval: falseproc sgplot data=logistic.ames_train; reg x = Gr_Liv_Area y = Bonus; title 'OLS for Binary Response?'; xaxis label='Greater Living Area (Sqft)'; yaxis label='Bonus Eligible';run;```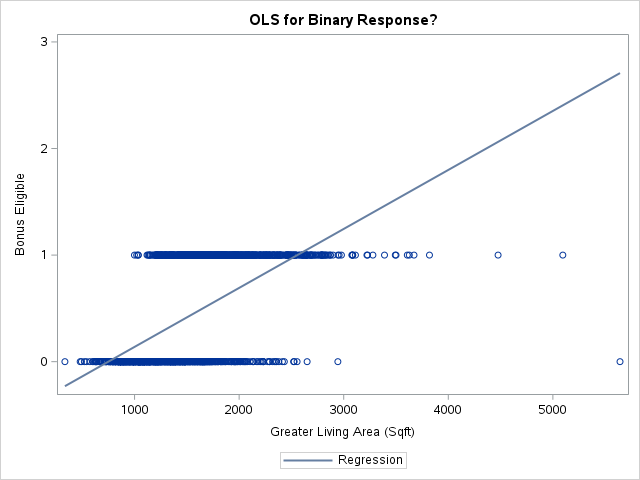{fig-align="center" width="6.67in"}Even though it doesn't appear to really look like our data, let's fit this linear probability model anyway for completeness sake.```{r}#| eval: falseproc reg data=logistic.ames_train plot(unpack)=diagnostics; model Bonus = Gr_Liv_Area;run;quit;```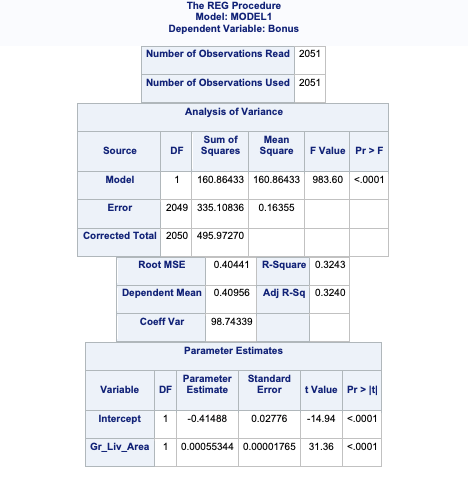{fig-align="center" width="6in"}{fig-align="center" width="6.67in"}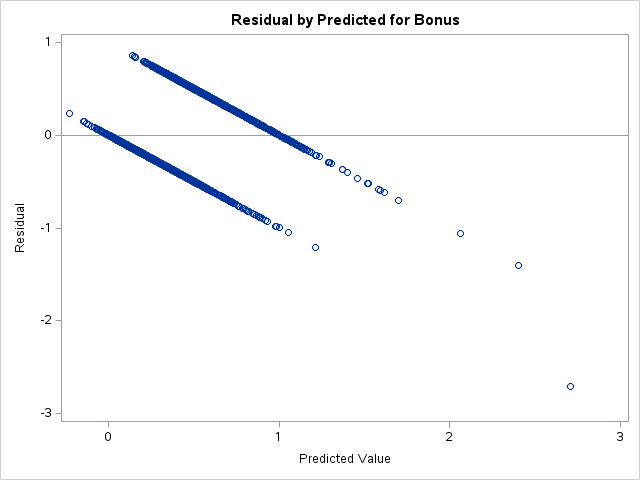{fig-align="center" width="6.67in"}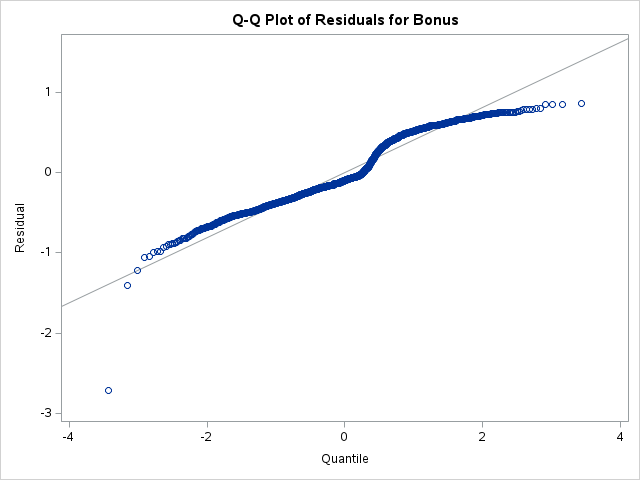{fig-align="center" width="6.67in"}As we can see from the charts above, the assumptions of ordinary least squares don't really hold in this situation. Therefore, we should be careful interpreting the results of the model. Maybe a better model won't have these problems?:::# Binary Logistic Regression ModelDue to the limitations of the linear probability model, people typically just use the binary logistic regression model. The logistic regression model does not have the limitations of the linear probability model. The outcome of the logistic regression model is the probability of getting a 1 in a binary variable, $E(y_i) = P(y_i = 1) = p_i$. That probability is calculated as follows:$$p_i = \frac{1}{1+e^{-(\beta_0 + \beta_1x_{1,i} + \cdots + \beta_k x_{k,i})}}$$This function has the desired properties for predicting probabilities. The predicted probability from the above equation will always be between 0 and 1. The parameter estimates do not enter the function linearly (this is a non-linear regression model), and the rate of change of the probability varies as the predictor variables vary as seen below.{fig-align="center" width="5in"}To create a linear model, a **link function** is applied to the probabilities. The specific link function for logistic regression is called the **logit** function.$$logit(p_i) = \log(\frac{p_i}{1-p_i}) = \beta_0 + \beta_1x_{1,i} + \cdots + \beta_k x_{k,i}$$The relationship between the predictor variables and the logits are linear in nature as the logits themselves are unbounded. This structure looks much more like our linear regression model structure. However, logistic regression does not use ordinary least squares (OLS) to estimate the coefficients in our model. OLS requires residuals which the logistic regression model does not provide. The target variable is binary in nature, but the predictions are probabilities. Therefore, we cannot calculate a traditional residual. Instead, logistic regression uses **maximum likelihood estimation**.Maximum likelihood estimation (MLE) is a very popular technique for estimating statistical models. It uses the assumed distribution (here logistic) to find the "most likely" values of the parameters to produce the data we see. In fact, it can be shown mathematically that the OLS solution in linear regression is the same as the MLE for linear regression. The likelihood function measures how probable a specific grid of $\beta$ values is to have produced your data, so we want to MAXIMIZE that as seen in the plot below.{fig-align="center" width="5in"}Let's see how to run binary logistic regression in each of our softwares!::: {.panel-tabset .nav-pills}## RThe `glm` function in R will provide us the ability to model binary logistic regressions. Similar to the `lm` function, you can specify a model formula. Notice the `factor` function on the *Central_Air* variable. This will convert this categorical variable into usable design variables for the modeling function.The `family = binomial(link = "logit")` option is there to specify that we are building a logistic model. Generalized linear models (GLM) are a general class of models where logistic regression is a special case where the link function is the logit function. Use the `summary` function to look at the necessary output.```{r}logit.model <-glm(Bonus ~ Gr_Liv_Area +factor(Central_Air), data = train, family =binomial(link ="logit"))summary(logit.model)```Let's examine the output above. Scanning down the output, you can see the actual logistic regression equation itself for each of the variables, including the design variable created for *Central_Air* with the `factor` function. At our significance level (we used an 0.005 significance level for this analysis based on the sample size) it appears that both of these variables are significant. We will address variable selection in the "Subset Selection and Diagnostics" section.To perform a global Likelihood Ratio Test to see if any of the variables are significant overall you can run the following code.```{r}logit.model.r <-glm(Bonus ~1, data = train, family =binomial(link ="logit"))anova(logit.model, logit.model.r, test ='LRT')```The above code creates a second model without any variables. It then performs a Likelihood Ratio Test (LRT) on this model compared to the original model. The results of this test show the usefulness of all the variables. This is comparable to the global F-test in linear regression. The two models are significantly different (based on our significance level) which implies that at least one of the variables is significant. If these models weren't significantly different then the variables would be adding no value statistically.For the *Central_Air* variable, we only have one design variable, but if our variable had 3 or more categories, we would have multiple design variables. Categorical variables should not be evaluated solely based on their individual categorical design variable significance as those represent specific tests between combinations of categories. The variable overall must be evaluated for its usefulness to the model. We will produce that with the next piece of code below to check the *Fireplaces* variable.```{r}logit.model.f <-glm(Bonus ~ Gr_Liv_Area +factor(Central_Air) +factor(Fireplaces), data = train, family =binomial(link ="logit"))car::Anova(logit.model.f, test ='LR', type ='III')```The above code creates a second model with the *Fireplaces* categorical variable. It then uses a different `Anova` function from the `car` package (notice the capital A in `Anova`). This function performs a LRT comparing a model with and without a variable but leaving every other variable in there. Notice the options for `test = 'LR'` to get the LRT as well as the `type = 'III'` to get the Type 3 LRTs. This just means that the test only drops that specific variable when comparing to the full model. The results of this test show the usefulness of the *Fireplaces* variable. The two models are significantly different (based on our significance level) which implies that the *Fireplaces* variable (the only difference between comparing a model with and without the *Fireplaces* variable) is significant as a whole. If these models weren't significantly different then the *Fireplaces* variable would be adding no value statistically.Lastly we can get the odds ratios for each of the above mentioned variables with the following code:```{r}#| message: falseexp(cbind(coef(logit.model), confint(logit.model)) )```Odds ratios are a great way of interpreting the output from a logistic regression. For example, let's look at the *Central_Air* variable odds ratio. This tells us that homes with central air are 52 times as likely (in terms of odds) of being bonus eligible, on average, then homes without central air. To practice interpreting continuous variables, let's look at the *Gr_Liv_Area* variable. Every additional square foot of living area leads to the home being 1.004 times as likely to be bonus eligible. This maybe a little harder to easily understand. Another way to put this would be that every additional square foot of living area increases the odds of the home being bonus eligible by 0.4% (100\*(1.004 - 1)) on average.## PythonThe `GLM.from_formula` function and the `fit` attribute in Python from the `statsmodels.genmod.generalized_linear_model` package will provide us the ability to model binary logistic regressions. With this function you can specify a model formula, similar to R. Notice the `C` function on the *Central_Air* variable. This will convert this categorical variable into usable design variables for the modeling function.The `family = Binomial()` option is there to specify that we are building a logistic model. Generalized linear models (GLM) are a general class of models where logistic regression is a special case where the link function is the logit function. Use the `summary` function to look at the necessary output.```{python}from statsmodels.genmod.families import Binomialfrom statsmodels.genmod.generalized_linear_model import GLMlog_model = GLM.from_formula('Bonus ~ Gr_Liv_Area + C(Central_Air)', data = train, family = Binomial()).fit()log_model.summary()```Let's examine the output above. Scanning down the output, you can see the actual logistic regression equation itself for each of the variables, including the design variable created for *Central_Air* with the `factor` function. At our significance level (we used an 0.005 significance level for this analysis based on the sample size) it appears that both of these variables are significant. We will address variable selection in the "Subset Selection and Diagnostics" section.Python also provides the Global Likelihood Ratio Test ('LLR p-value' in the output). The results of this test show the usefulness of all the variables. This is comparable to the global F-test in linear regression. The two models are significantly different (based on our significance level of 0.005) which implies that at least one of the variables is significant. If these models weren't significantly different then the variables would be adding no value statistically.For the *Central_Air* variable, we only have one design variable, but if our variable had 3 or more categories, we would have multiple design variables. Categorical variables should not be evaluated solely based on their individual categorical design variable significance as those represent specific tests between combinations of categories. The variable overall must be evaluated for its usefulness to the model. We will produce that with the next piece of code below to check the *Fireplaces* variable.```{python}reduced_ll = log_model.llffull_ll = smf.logit("Bonus ~ Gr_Liv_Area + C(Central_Air) + C(Fireplaces)", data = train).fit().llf```Now we have the likelihood values from the original model without fireplace using the `llf` attribute from the `log_model` object and the likelihood values from a model with the addition of the *Fireplaces* variable. From there we can calculate the LRT by hand using the code below.```{python}import scipy as spLR_statistic =-2*(reduced_ll-full_ll)print(LR_statistic)p_val = sp.stats.chi2.sf(LR_statistic, 4)print(p_val)```The above code performs a LRT comparing a model with and without a variable but leaving every other variable in there. Notice the 4 degrees of freedom in the `sp.stats.chi2.sf` function. This is because of the 5 values for the *Fireplaces* variable. The degrees of freedom is the difference in number of $\beta$ coefficients between the two models. If *Fireplaces* has 5 levels, then we only need 4 variables in our regression. The results of this test show the usefulness of the *Fireplaces* variable. The two models are significantly different (based on our significance level) which implies that the *Fireplaces* variable (the only difference between comparing a model with and without the *Fireplaces* variable) is significant as a whole. If these models weren't significantly different then the *Fireplaces* variable would be adding no value statistically.Lastly we can get the odds ratios for each of the above mentioned variables with the following code:```{python}import numpy as npnp.exp(log_model.params[1:3])```Odds ratios are a great way of interpreting the output from a logistic regression. For example, let's look at the *Central_Air* variable odds ratio. This tells us that homes with central air are 52 times as likely (in terms of odds) of being bonus eligible, on average, then homes without central air. To practice interpreting continuous variables, let's look at the *Gr_Liv_Area* variable. Every additional square foot of living area leads to the home being 1.004 times as likely to be bonus eligible. This maybe a little harder to easily understand. Another way to put this would be that every additional square foot of living area increases the odds of the home being bonus eligible by 0.4% (100\*(1.004 - 1)) on average.```{python}100*(np.exp(log_model.params[1:3]) -1)```## SASPROC LOGISTIC has a built in CLASS statement. This allows us to input categorical variables easily into our logistic regression. The *Central_Air* variable had 2 categories - Y and N. We will use the N as our reference category as you can see with the `ref =` option listed after the *Central_Air* variable. By default, SAS uses effects coding for all categorical variables. To switch to reference coding we use the `param = ref` option at the end of the CLASS statement.For our odds ratios as well as parameter estimates, the profile likelihood estimation method is preferred to the Wald approximation. This is accomplished by using the `clodds = pl` and `clparm = pl` options.```{r}#| eval: falseproc logistic data=logistic.ames_train plots(only)=(oddsratio); class Central_Air(ref='N') / param=ref; model Bonus(event='1') = Gr_Liv_Area Central_Air / clodds=pl clparm=pl; title 'Modeling Bonus Eligibility';run;quit;```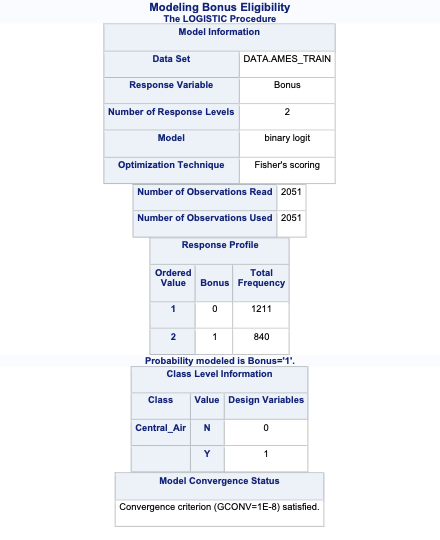{fig-align="center" width="6in"}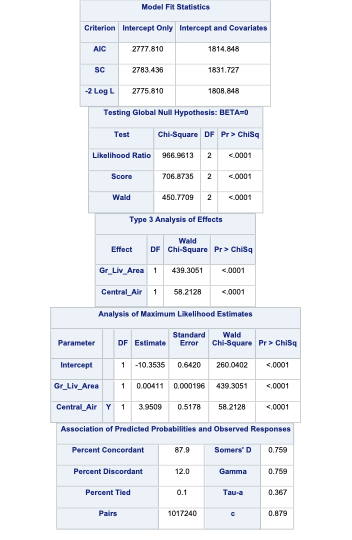{fig-align="center" width="6in"}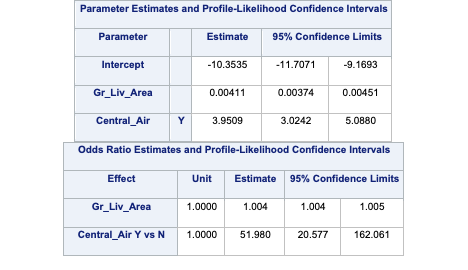{fig-align="center" width="6in"}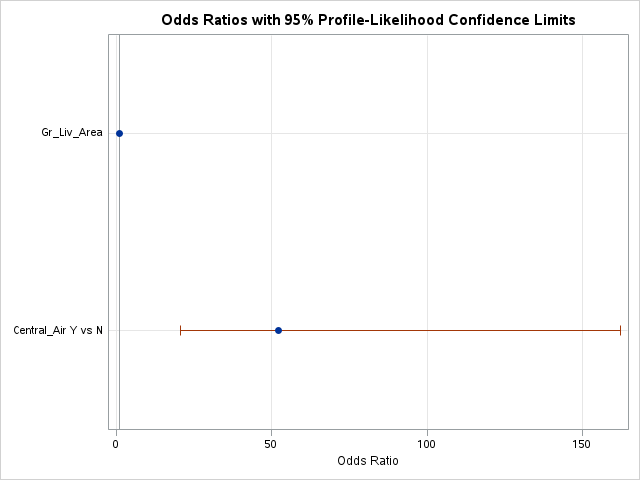{fig-align="center" width="6.67in"}Let's examine the output above. Scanning down the output, you can see that SAS provided us with a summary of the number of observations read and used in the analysis as well as a frequency breakdown of the target variable.The important piece of the output here is the **model convergence status**. Note that the model converged. This estimation is done through maximum likelihood estimation (MLE) so we need this convergence. We will address what happens when this doesn't converge in the "Data Considerations" section.SAS then provides some basic model metrics like the AIC and SC as well as the Global Likelihood Ratio Test. The small p-value here (we used an 0.005 significance level for this analysis based on the sample size) implies that at least one of the variables is useful in the prediction of bonus eligibility. The Type 3 Analysis table provides us with a variable by variable breakdown to see which of the variables prove helpful. At our significance level it appears that the variables are both significant. We will address variable selection in the "Subset Selection and Diagnostics" section.The MLE table provides us with the actual logistic regression equation itself for each of the variables, including the design variables created for *Central_Air* with the CLASS statement.The Association of Predicted Probabilities table provides us with many model metrics that we will discuss in the "Model Assessment" section.Lastly we are provided with the odds ratios for each of the above mentioned variables. Odds ratios are a great way of interpreting the output from a logistic regression. For example, let's look at the *Central_Air* variable odds ratio. This tells us that homes with central air are 52 times as likely (in terms of odds) of being bonus eligible, on average, then homes without central air. To practice interpreting continuous variables, let's look at the *Gr_Liv_Area* variable. Every additional square foot of living area leads to the home being 1.004 times more likely to be bonus eligible. This maybe a little harder to easily understand. Another way to put this would be that every additional square foot of living area increases the odds of the home being bonus eligible by 0.4% (100\*(1.004 - 1)) on average.:::# Testing AssumptionsOutside of independence of observations, the biggest assumption of logistic regression is that the continuous predictor variables are linearly related to the logit function (our transformation of the probability of our target). A great way to check this assumption is through Generalized Additive Models (GAMs).Generalized additive models (GAM's) can be used to help evaluate the linearity of the relationship between the continuous predictor variables and the logit. When GAM's are applied to a logistic regression, the following is the new model:$$\log(\frac{p_i}{1-p_i}) = \beta_0 + f_1(x_1) + \cdots + f_k(x_k)$$ These functions applied to the continuous predictor variables need to be estimated. GAM's use spline functions to estimate these. If these splines say a straight line is good, then the assumption is met. There are some options if the assumption is not met:1. Use the GAM representation of the logistic regression model instead of the traditional logistic regression model.2. Strategically bin the continuous predictor variable.In the first approach, instead of using the logistic regression model as previously defined, the logistic GAM would be used for predictions. The GAM version of the logistic regression is less interpretable in the traditional sense of odds ratios. Instead, plots are used to show potentially complicated relationships.In the second approach, the continuous variables are categorized and put in the original logistic framework in their categorical form. There are statistical approaches to doing this, but one could also use the GAM plots to decide on possible splits for binning the data.Let's see how to produce GAMs in each of our softwares!::: {.panel-tabset .nav-pills}## RFor GAMs we can use the `gam` function in R. Similar to the `glm` function, you have a model formula to specify the full model. Categorical variables can still be handled with the `factor` function. The only difference is that we will test the continuous variables with splines to see if those splines produce anything significantly better than their linear representations. The `s` function is put on every one of the continuous variables. The `family =` and `link =` options are used to specify the logistic regression. The `method =` option is specified here as their are multiple approaches to fitting the GAM in R. We will use the `REML` approach.```{r}#| message: falselibrary(mgcv)fit.gam <- mgcv::gam(Bonus ~s(Gr_Liv_Area) +factor(Central_Air),data = train, family =binomial(link ='logit'),method ='REML')summary(fit.gam)plot(fit.gam)```From the above output we can see that *Gr_Liv_Area* and *Central_Air* are both still significant in this model. However, now the *Gr_Liv_Area* variable is a more complicated transformation. As seen in the graph above, it appears that *Gr_Liv_Area* has a nonlinear pattern with the logit. In fact, the `edf` (or estimated degrees of freedom) in the output above also shows us this. If the `edf` value was 1, the best spline was a linear relationship with the target (linearity assumption holds). However, since it is not equal to 1, we cannot say this. How close is close enough to 1? If you wanted a statistical test, we could compare a model with a linear representation of *Gr_Liv_Area* to the spline version with a Likelihood Ratio test.```{r}anova(logit.model, fit.gam, test="LRT")```The null hypothesis to the above test is that the two models are equal. This null hypothesis would imply that the linearity assumption would hold since the spline is not estimating anything more complicated. However, the p-value was extremely small and therefore the two models are *not* equal to other. This means that *Gr_Liv_Area* cannot just be modeled linearly with the logit.From the plot above, it appears that *Gr_Liv_Area* has three main patterns - below 1300 sqft, between 1300 and 4000 sqft, and above 4000 sqft. But we want bins that are about the same in their effect. Let's create a new variable along the cut points of \< 1000, 1000-1500, 1500-3000, 300-4500, 4500+.```{r}train <- train %>%mutate(Gr_Liv_Area_BIN =cut(Gr_Liv_Area, breaks =c(-Inf,1000,1500,3000,4500,Inf)))```Now let's rebuild the logistic regression model with this new categorical version of the *Gr_Liv_Area* variable.```{r}logit.model.bin <-glm(Bonus ~factor(Gr_Liv_Area_BIN) +factor(Central_Air),data = train, family =binomial(link ='logit'))summary(logit.model.bin)```From the above output, we can see that *Gr_Liv_Area_BIN* is still a significant variable in our model. The nice part about using a categorical representation for the variable instead of using the GAM for predictions is that we still have some interpretability on this variable using odds ratios for the categories.## PythonFor GAMs we can use the `GLMGam.from_formula` function in Python. Similar to the `GLM.from_formula` function, you have a model formula to specify the full model. Categorical variables can still be handled with the `C` function. The only difference is that we will test the continuous variables with splines to see if those splines produce anything significantly better than their linear representations. The `BSplines` function is put on every one of the continuous variables and then added into the `smoother` option in the `GLMGam` function. The `family =` option is used to specify the logistic regression.```{python}import statsmodels as smfrom statsmodels.gam.api import GLMGam, BSplinesx_spline = train['Gr_Liv_Area']bs = BSplines(x_spline, df =5, degree =3)gam_model = GLMGam.from_formula('Bonus ~ C(Central_Air)', data = train, smoother = bs, family = sm.api.families.Binomial()).fit()gam_model.summary()``````{python}gam_model.plot_partial(smooth_index =0)plt.show()```From the above output we can see that *Gr_Liv_Area* and *Central_Air* are both still significant in this model. However, now the *Gr_Liv_Area* variable is a more complicated transformation. As seen in the graph above, it appears that *Gr_Liv_Area* has a nonlinear pattern with the logit. If you wanted a statistical test, we could compare a model with a linear representation of *Gr_Liv_Area* to the spline version with a Likelihood Ratio test to see if any value is added from the spline.```{python}reduced_ll = log_model.llffull_ll = gam_model.llfLR_statistic =-2*(reduced_ll-full_ll)print(LR_statistic)p_val = sp.stats.chi2.sf(LR_statistic, 3)print(p_val)```The null hypothesis to the above test is that the two models are equal. This null hypothesis would imply that the linearity assumption would hold since the spline is not estimating anything more complicated. However, the p-value was extremely small and therefore the two models are *not* equal to other. This means that *Gr_Liv_Area* cannot just be modeled linearly with the logit.From the plot above, it appears that *Gr_Liv_Area* has three main patterns - below 1300 sqft, between 1300 and 4000 sqft, and above 4000 sqft. But we want bins that are about the same in their effect. Let's create a new variable along the cut points of \< 1000, 1000-1500, 1500-3000, 300-4500, 4500+ with the `cut` function.```{python}import pandas as pdtrain['Gr_Liv_Area_BIN'] = pd.cut(train['Gr_Liv_Area'], [0, 1000, 1500, 3000, 4500, 10000])```Now let's rebuild the logistic regression model with this new categorical version of the *Gr_Liv_Area* variable.```{python}log_model_bin = smf.logit("Bonus ~ C(Gr_Liv_Area_BIN) + C(Central_Air)", data = train).fit()log_model_bin.summary()```From the above output, we can see that *Gr_Liv_Area_BIN* is still a significant variable in our model. The nice part about using a categorical representation for the variable instead of using the GAM for predictions is that we still have some interpretability on this variable using odds ratios for the categories.## SASFor GAMs we can use PROC GAM. Similar to PROC LOGISTIC, we fit our MODEL statement with our full model. PROC GAM even has a CLASS statement for categorical variables. The only difference is that we will test the continuous variables with splines to see if those splines produce anything significantly better than their linear representations. The `spline` option is put on every one of the continuous variables. We want to leave the categorical variables alone so use the `param` option on those. The `dist =` and `link =` options are used to specify the logistic regression.The `ods` statement here selects only the significance of the splines (`ANODEV` option) and the component plots (`SmoothingComponentPlot` option) since that is all we desire to test the assumption.```{r}#| eval: falseods html select ANODEV SmoothingComponentPlot;proc gam data=logistic.ames_train plots =components(clm commonaxes); class Central_Air(ref='N') / param = ref; model Bonus(event='1') =spline(Gr_Liv_Area, df =2) param(Central_Air) / dist = binomial link = logit;run;quit;```{fig-align="center" width="6in"}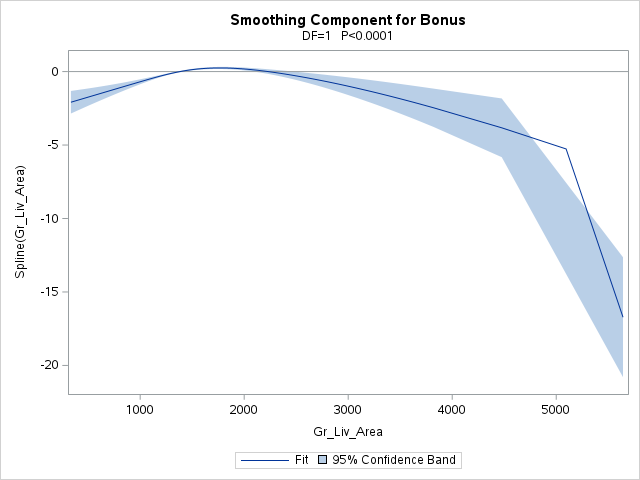{fig-align="center"}Here we can see that the relationship with *Gr_Liv_Area* is more complicated than just linear in terms of its relationship with the logit. If we saw a straight line here we would be able to conclude the linearity assumption held.From the plot above, it appears that *Gr_Liv_Area* has three main patterns - below 1300 sqrt, between 1300 and 4000 sqft, and above 4000 sqft. But we want bins that are about the same in their effect. Let's create a new variable along the cut points of \< 1000, 1000-1500, 1500-3000, 300-4500, 4500+.```{r}#| eval: falseproc format;value Gr_Liv_AreaFMT low -<1000="Small"1000-<1500="Small-Medium"1500-<3000="Medium"3000-<4500="Medium-Large"4500- high ="Large";run;proc logistic data=logistic.ames_train plots(only)=(oddsratio); format Gr_Liv_Area Gr_Liv_AreaFMT.; class Central_Air(ref='N') Gr_Liv_Area / param=ref; model Bonus(event='1') = Gr_Liv_Area Central_Air / clodds=pl clparm=pl; title 'Modeling Bonus Eligibility';run;quit;```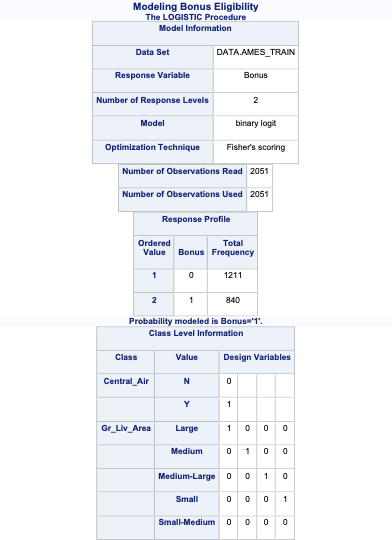{fig-align="center" width="6in"}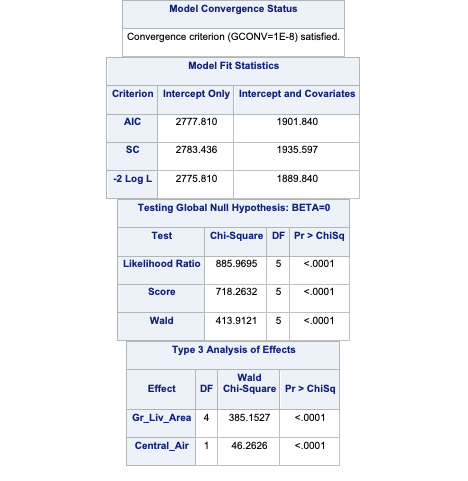{fig-align="center" width="6in"}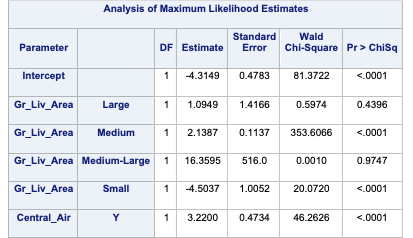{fig-align="center" width="6in"}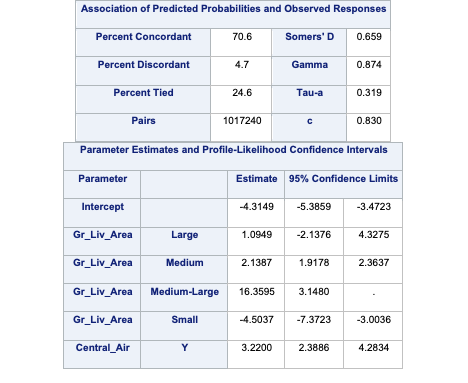{fig-align="center" width="6in"}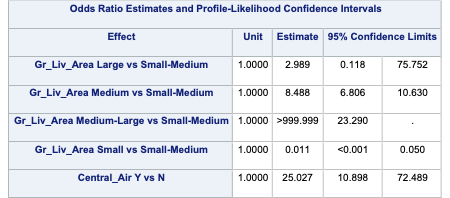{fig-align="center" width="6in"}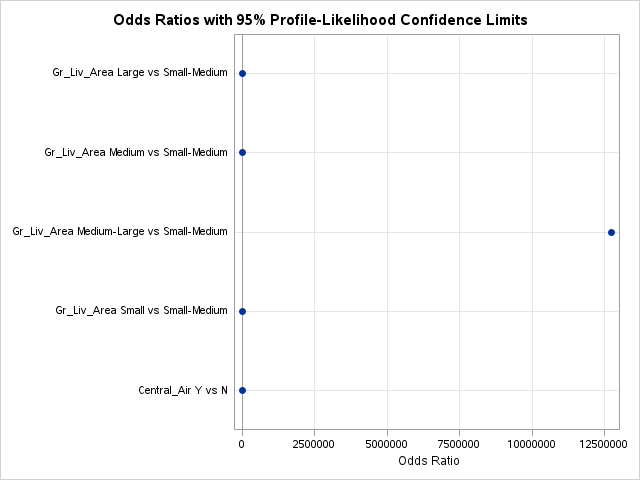{fig-align="center" width="6.67in"}From the above output, we can see that the binned version of *Gr_Liv_Area* is still a significant variable in our model. The nice part about using a categorical representation for the variable instead of using the GAM for predictions is that we still have some interpretability on this variable using odds ratios for the categories.:::# Predicted ValuesObviously, the predicted logit values really don't help us too much. Instead we want to gather the predicted probabilities of the target variable categories. Luckily, the software we are looking at make this rather easy to do.Let's see how to produce these predicted probabilities in each of our softwares!::: {.panel-tabset .nav-pills}## RIf you split your data into training and validation (and/or testing) you could score that data set using the `predict` function. Here we are creating a new data set of 5 observations to score instead. The `predict` function has three primary pieces - the model object (here called `logit.model`, the `newdata =` option, and the `type =` option. The `newdata =` option is where you specify the data set you want scored, while the `type =` option specifies the type of prediction you want. Here we want the `response` option since we are predicting the probabilities. If we wanted the predicted logit values we could use the option `terms` instead.The `visreg` function below creates the effect plot, which will show us the logistic curve across different values of the continuous variable, here *Gr_Liv_Area*. It will show each of the categorical variable categories as a separate curve. If there is were more continuous variables they are just taken at a specified value - their average value.```{r}new_ames <-data.frame(Gr_Liv_Area =c(1500, 2000, 2250, 2500, 3500),Central_Air =c("N", "Y", "Y", "N", "Y"))new_ames <-data.frame(new_ames, 'Pred'=predict(logit.model, newdata = new_ames, type ="response"))library(visreg)visreg(logit.model, "Gr_Liv_Area", by ="Central_Air", scale ="response",overlay =TRUE,xlab ='Greater Living Area (Sqft)',ylab ='Bonus Eligibility')print(new_ames)```The `print` function above looks at the scored data set. Notice that we added an additional column to our original data set we were scoring. This is the predicted probability of a 1. This is default in R. If you want the predicted probability of the 0 category, you can just subtract this prediction from 1.## PythonIf you split your data into training and validation (and/or testing) you could score that data set using the `predict` function. Here we are creating a new data set of 5 observations to score instead. The `predict` function on the model object (here called `log_model`) just needs the dataset to be scored (here called `new_ames`). By default, the predict function gives the predicted probabilities.```{python}new_data = [[1500, 'N'], [2000, 'Y'], [2250, 'Y'], [2500, 'N'], [3500, 'Y']]new_ames = pd.DataFrame(new_data, columns = ['Gr_Liv_Area', 'Central_Air'])new_ames['Pred'] = log_model.predict(new_ames)print(new_ames)```The `print` function above looks at the scored data set. Notice that we added an additional column to our original data set we were scoring. This is the predicted probability of a 1. This is default in Python. If you want the predicted probability of the 0 category, you can just subtract this prediction from 1.The `regplot` function below creates the effect plot, which will show us the logistic curve across different values of the continuous variable, here *Gr_Liv_Area*. We overlay two of these curves, one for each of the categories of *Central_Air*. If there is were more continuous variables they are just taken at a specified value - their average value.```{python}plt.cla()fig, ax = plt.subplots()sns.regplot(data = train[train['Central_Air'] =='Y'], x ='Gr_Liv_Area', y ='Bonus', scatter =True, logistic =True, ax = ax)sns.regplot(data = train[train['Central_Air'] =='N'], x ='Gr_Liv_Area', y ='Bonus', scatter =True, logistic =True, ax = ax)plt.show()```## SASIf you split your data into training and validation (and/or testing) you could score that data set using PROC LOGISTIC's built in SCORE statement. Here we are creating a new data set of 5 observations to score instead. The SCORE statement has two primary pieces - `data =` and `out =`. The `data =` piece is where you specify the data set you want scored, while the `out =` piece is the name of the new scored data set.The `ods` statement below only selects the effect plot, which will show us the logistic curve across different values of the first continuous variable, here *Gr_Liv_Area*. It will show each of the categorical variable categories as a separate curve. The other continuous variables are just taken at their average value.```{r}#| eval: falsedata new_ames; input Gr_Liv_Area Central_Air $; datalines;1500 N2000 Y2250 Y2500 N3500 Y ;run;ods html select EFFECTPLOT;proc logistic data=logistic.ames_train plots(only)=(oddsratio effect); class Central_Air(ref='N') / param=ref; model Bonus(event='1') = Gr_Liv_Area Central_Air / clodds=pl clparm=pl; title 'Modeling Bonus Eligibility'; score data=new_ames out=ames_scored;run;quit;proc print data=ames_scored;run;```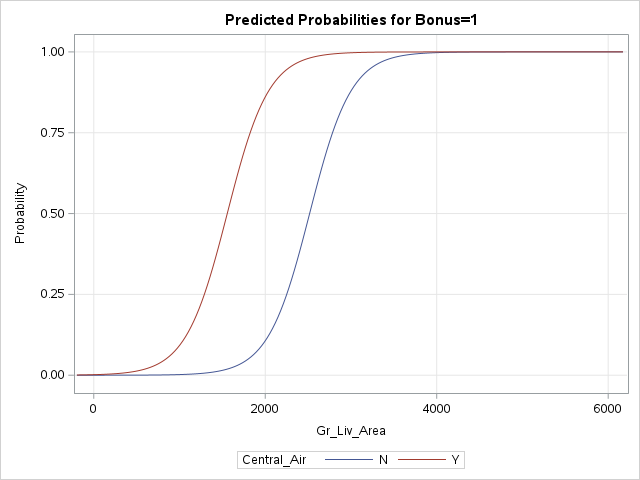{fig-align="center" width="6.67in"}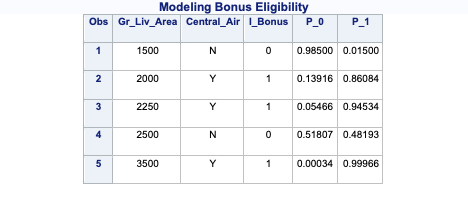{fig-align="center" width="6in"}The PROC PRINT above looks at the scored data set. Notice that there are four additional columns that we have on our original data set we were scoring. The first two, *F_Bonus* and *I_Bonus*, represent the original target variable and the predicted target variable respectively. Specifically, they stand for *FROM* and *INTO*. SAS decides the predicted category rather crudely by assuming if the predicted probability of the category is above 0.5, then it predicts that category will occur. We will see in the "Model Assessment" section that 0.5 is rarely the optimal cut-off.The final two categories are the predicted probabilities for each of the values of the target variable - *P_0* and *P_1*. These are just the predicted probability of 0 and 1 in our target variable respectively.:::