Feature creation and selection is one of the most important pieces to any modeling process. It is no different for credit score modeling. Before selecting the variables, we need to transform them. Specifically in credit score modeling, we need to take our continuous variables and bin them into categorical versions.
Variable Grouping
Scorecards end up with only just bins within a variable. There are two primary objectives when deciding on how to bin the variables:
Eliminate weak variables or those that do not conform to good business logic.
Group the strongest variables’ attribute levels (values) in order to produce a model in the scorecard format.
Binning continuous variables help simplify analysis. We no longer need to explain coefficients that imply some notion of constant effect or linearity, but instead are just comparisons of categories. This process of binning also models non-linearity in an easily interpretable way. We are not restricted to linearity of the continuous variables as some models assume. Outliers are also easily accounted for as they are typically contained within the smallest or largest bin. Lastly, missing values are no longer a problem and do not need imputation. Missing values can get their own bin making all observations available to be modeled.
There are a variety of different approaches to statistically bin variables. We will focus on the two most popular ones here:
Prebinning and Combining of Bins
Decision / Conditional Inference Trees
The first is by prebinning the variables followed by the grouping of these bins. Imagine you had a variable whose range is from 3 to 63. This approach would first break this variable into quantile bins. Softwares typically use anywhere from 20 to 100 equally sized quantiles for this initial step. From there, we use chi-square tests to compare each adjacent pair of bins. If the bins are statistically the same with respect to the target variable using two by two contingency table Chi-square tests (Mantel-Haenzel for example), then we combine the bins. We repeat this process until no more adjacent pairs of bins can be statistically combined. Below is a visual of this process.
The second common approach is through decision / conditional inference trees. The classical CART decision tree uses the Gini statistic to find the best splits for a single variable predicting the target variable. In this scenario, you have one single predictor variable as the only variable in the decision tree. Each possible split is evaluated and determined based on the Gini statistic to make the split that occurs have the highest measure of purity. This process is repeated until no further splits are possible. An example of this is show below.
Some softwares and packages use conditional inference trees instead of decision trees. These are a variation on the common CART decision tree. CART methods for decision trees potentially have inherent bias - variables with more levels are more likely to be split on if split using the Gini and entropy criterion. Conditional inference trees on the other hand add an extra step to this process. Conditional inference trees evaluate which variable is most significant first, then evaluate what is the best split of a continuous variable through the Chi-square decision tree approach on that specific variable only, not all variables. They repeat this process until no more significant places in the variable are left to be split. How does this apply to binning though? When binning a continuous variable, we are predicting the target variable using only our one continuous variable in the conditional inference tree. It evaluates if the variable is significant at predicting the target variable. If so, it finds the most significant statistical split using Chi-square tests in between each value of the continuous variable and then comparing the two groups formed by this split. After finding the most significant split you have two continuous variables - one below the split and one above. The process repeats itself until the algorithm can no longer find significant splits leading to the definition of your bins. Below is a visual of this process.
Cut-offs (or cut points) from the decision tree algorithms might be rather rough. Sometimes we override the automatically generated cut points to more closely conform to business rules. These overrides might make the bins sub-optimal, but hopefully not too much to impact the analysis.
Imagine a similar scenario for linear regression. Suppose you had two models with the first model having an \(R^2 = 0.8\) and the second model having an \(R^2 = 0.78\). However, the second model made more intuitive business sense than the first. You would probably choose the second model willing to sacrifice a small amount of predictive power for a model that made more intuitive sense. The same can be thought of when slightly altering the bins from these two approaches described above.
Let’s see how each of our softwares approaches binning continuous variables!
Before any binning is done, we need to split our data into training and testing because the binning evaluates relationships between the target variable and the predictor variables. This is easily done in Python using the train_test_split function from sklearn and the model_selection package. The test_size = option identifies the proportion of observations to be sampled and put in the test dataset. It was set as 25% of the number of rows in the dataset. The random_state = option specifies the seed so we can reproduce our results. Lastly, we use the head element of our dataframe to look at the first 5 rows.
Code
import pandas as pdfrom sklearn.model_selection import train_test_splittrain, test = train_test_split(accepts, test_size =0.25, random_state =1234)train.head(n =5)
Now that we have our dataset, we can start binning. The function OptBinning from the optbinning package can do either of the approaches detailed above. It also provides an additional layer of optimization on top of the approaches so it can try to maximize metrics of fit with the bins. By default, it maximizes the information value (IV) discussed in the sections below. We will look at binning the bureau_score variable with the bad target variable. The OptBinning function asks for the name and data type (dtpye = option) of the variable we are binning. Next, we use the .fit capabilities on our predictor and target variable (saved as X and y). The splits function reports the splits of the variable.
Code
import numpy as npfrom optbinning import OptimalBinning
(CVXPY) Dec 19 04:35:35 PM: Encountered unexpected exception importing solver GLOP:
RuntimeError('Unrecognized new version of ortools (9.11.4210). Expected < 9.10.0. Please open a feature request on cvxpy to enable support for this version.')
(CVXPY) Dec 19 04:35:35 PM: Encountered unexpected exception importing solver PDLP:
RuntimeError('Unrecognized new version of ortools (9.11.4210). Expected < 9.10.0. Please open a feature request on cvxpy to enable support for this version.')
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
To see more metrics about each of the splits we can use the binning_table function and build() capabilities to view the metrics. There are a lot of metrics in this table that are discussed in the next section.
The R package that you choose will determine the technique that is used for the binning of the continuous variables. The scorecard package more closely aligns with the approach of prebinning the variable and combining the bins. The smbinning package as shown below uses the conditional inference tree approach.
The smbinning function inside the smbinning package is the primary function to bin continuous variables. Our data set has a variable bad that flags when an observation has a default. However, the smbinning function needs a variable that defines the people in our data set that did not have the event - those who did not default. Below we create this new good variable in our training data set.
Code
train$good <-abs(train$bad -1)table(train$good)
0 1
900 3477
We also need to make the categorical variables in our data set into factor variables in R so the function will not automatically assume they are numeric just because they have numerical values. We can do this with the as.factor function.
Now we are ready to bin our variables. Let’s go through an example of binning the bureau_score variable using the smbinning function. The three main inputs to the smbinning function are the df = option which defines the data frame for your data, the y = option that defines the target variable by name, and the x = option that defines the predictor variable to be binned by name. To observe where the splits took place we can look at the ivtable or cut elements from our results. We will discuss all the values in the ivtable output in the next section.
Code
library(smbinning)
Loading required package: sqldf
Loading required package: gsubfn
Loading required package: proto
Loading required package: RSQLite
Loading required package: partykit
Loading required package: grid
Loading required package: libcoin
Loading required package: mvtnorm
Loading required package: Formula
Code
result <-smbinning(df = train, y ="good", x ="bureau_score")result$ivtable
Weight of evidence (WOE) measures the strength of the attributes (bins) of a variable in separating events and non-events in a binary target variable. In credit scoring, that implies separating bad and good accounts respectively.
Weight of evidence is based on comparing the proportion of goods to bads at each bin level and is calculated as follows for each bin within a variable:
The distribution of goods for each bin is the number of goods in that bin divided by the total number of goods across all bins. The distribution of bads for each bin is the number of bads in that bin divided by the total number of bads across all bins. An example is shown below:
WOE summarizes the separation between events and non-events (bads and goods) as shown in the following table:
For WOE we are looking for big differences in WOE between bins.
Ideally, we would like to see monotonic increases for variables that have ordered bins. This isn’t always required as long as the WOE pattern in the bins makes business sense. However, if a variable’s bins go back and forth between positive and negative WOE values across bins, then the variable typically has trouble separating goods and bads. Graphically, the WOE values for all the bins in the bureau_score variable look as follows with the line plot below:
The histogram in the plot above also displays the distribution of events and non-events as the WoE values are changing. WOE approximately zero implies the distribution of non-events (goods) are approximately equal to the distribution of events (bads) so that bin doesn’t do a good job of separating these events and non-events. WOE of positives values implies the bin identifies observations that are non-events (goods), while WOE of negative values implies bin identifies observations that are events (bads).
One quick side note. WOE values can take a value of infinity or negative infinity when quasi-complete separation exists in a category (zero events or non-events). Some people adjust the WOE calculation to include a small smoothing parameter to make the numerator or denominator of the WOE calculation not equal to zero.
Let’s see how to get the weight of evidence values in each of our softwares!
The function OptBinning from the optbinning package can do either of the approaches detailed above. It also provides an additional layer of optimization on top of the approaches so it can try to maximize metrics of fit with the bins. We will look at binning the bureau_score variable with the good target variable. The OptBinning function asks for the name and data type (dtpye = option) of the variable we are binning. Next, we use the .fit capabilities on our predictor and target variable (saved as x and y). To see more metrics about each of the splits we can use the binning_table function and build() capabilities to view the metrics.
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
The weight of evidence values are listed in the WoE column and follow a similar calculation although we used different bin values for the hand calculation above. We can easily get the plot of the WOE values using the .plot function with the metric = "woe" option. The resulting plot is the same as the WOE plot above.
Code
iv_table.plot(metric ="woe")
You can get weight of evidence values for a factor variable as well without needing to rebin the values. This is done using the OptBinning function on the purpose variable as shown below, now with a dtype = option set to categorical:
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
The smbinning function inside the smbinning package is the primary function to bin continuous variables. Let’s go through an example of binning the bureau_score variable using the smbinning function. The three main inputs to the smbinning function are the df = option which defines the data frame for your data, the y = option that defines the target variable by name, and the x = option that defines the predictor variable to be binned by name.
As we previously saw, the ivtable element contains a summary of the splits as well as some information regarding each split including weight of evidence.
Code
result <-smbinning(df = train, y ="good", x ="bureau_score")result$ivtable
The weight of evidence values are listed in the WoE column and the same values as shown above. We can easily get the plot of the WOE values using the smbinning.plot function with the option = "WoE" option.
You can get weight of evidence values for a factor variable as well without needing to rebin the values. This is done using the smbinning.factor function on the purpose variable as shown below:
Code
result <-smbinning.factor(df = train, y ="good", x ="purpose")result$ivtable
Cutpoint CntRec CntGood CntBad CntCumRec CntCumGood CntCumBad PctRec
1 = 'LEASE' 1458 1170 288 1458 1170 288 0.3331
2 = 'LOAN' 2919 2307 612 4377 3477 900 0.6669
3 Missing 0 0 0 4377 3477 900 0.0000
4 Total 4377 3477 900 NA NA NA 1.0000
GoodRate BadRate Odds LnOdds WoE IV
1 0.8025 0.1975 4.0625 1.4018 0.0503 0.0008
2 0.7903 0.2097 3.7696 1.3270 -0.0246 0.0004
3 NaN NaN NaN NaN NaN NaN
4 0.7944 0.2056 3.8633 1.3515 0.0000 0.0012
Information Value (IV) & Variable Selection
Weight of evidence summarizes the individual categories or bins of a variable. However, we need a measure of how well all the categories in a variable do at separating the events from non-events. That is what information value (IV) is for. IV uses the WOE from each category as a piece of its calculation:
\[
IV = \sum_{i=1}^L (Dist.Good_i - Dist.Bad_i)\times \log(\frac{Dist.Good}{Dist.Bad})
\]
In credit modeling, IV is used in some instances to actually select which variables belong in the model. Here are some typical IV ranges for determining the strength of a predictor variable at predicting the target variable:
\(0 \le IV < 0.02\) - Not predictor
\(0.02 \le IV < 0.1\) - Weak predictor
\(0.1 \le IV < 0.25\) - Moderate (medium) predictor
\(0.25 \le IV\) - Strong predictor
Variables with information values greater than 0.1 are typically used in credit modeling.
Some resources will say that IV values greater than 0.5 might signal over-predicting of the target. In other words, maybe the variable is too strong of a predictor because of how that variable was originally constructed. For example, if all previous loan decisions have been made only on bureau score, then of course that variable would be highly predictive and possibly the only significant variable. In these situations, good practice is to build one model with only bureau score and another model without bureau score but with other important factors. We then ensemble these models together.
Let’s see how to get the information values for our variables in each of our softwares!
The function OptBinning from the optbinning package can do either of the approaches detailed above. It also provides an additional layer of optimization on top of the approaches so it can try to maximize metrics of fit with the bins. We will look at binning the bureau_score variable with the good target variable. The OptBinning function asks for the name and data type (dtpye = option) of the variable we are binning. Next, we use the .fit capabilities on our predictor and target variable (saved as X and y). To see more metrics about each of the splits we can use the binning_table function and build() capabilities to view the metrics.
As we previously saw, the binning_table element contains a summary of the splits as well as some information regarding each split including information value.
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
The information value is listed in the IV column. The IV numbers in each of the rows for the bins is the component of the IV from each of the categories. The final row is the sum of the previous rows which is the overall variable IV.
Another way to view the information value for every variable in the dataset is to use the BinningProcess function. The main input to this function is the list of column names you want evaluated. We have training data selected without the target variable, bad, or the weighting variable, weight. The categorical_variables = option is used to specify which variables in the data are categorical instead of continuous. We can also use the selection_criteria option to define what variables we would want to include in a follow-up model. Here, we are only choosing the variables with IV values above 0.1. We then use the same .fit format where you define the variables with the X object and the y object to define the target variable. The function then calculates the IV for each variable in the dataset with the target variable.
To view these information values for each variable we can just print out a table of the results by calling the summary object. Here we just print out the splits with the IV values instead of all the summary statistics.
As we can see from the output above, the strong predictors of default are bureau_score, tot_rev_line, rev_util, and age_oldest_tr. The moderate or medium predictors are tot_derog, ltv, tot_tr, tot_rev_debt, down_pyt, tot_income, and tot_rev_tr. These would be the variables typically used in credit modeling due to having IV scores above 0.1.
The smbinning function inside the smbinning package is the primary function to bin continuous variables. Let’s go through an example of binning the bureau_score variable using the smbinning function. The three main inputs to the smbinning function are the df = option which defines the data frame for your data, the y = option that defines the target variable by name, and the x = option that defines the predictor variable to be binned by name.
As we previously saw, the ivtable element contains a summary of the splits as well as some information regarding each split including information value.
Code
result <-smbinning(df = train, y ="good", x ="bureau_score")result$ivtable
The information value is listed in the IV column and the last row. The IV numbers in each of the rows for the bins is the component of the IV from each of the categories. The final row is the sum of the previous rows which is the overall variable IV.
Another way to view the information value for every variable in the dataset is to use the smbinning.sumiv function. The only two inputs to this function are the data = option where you define the dataset and the y = option to define the target variable. The function then calculates the IV for each variable in the dataset with the target variable.
To view these information values for each variable we can just print out a table of the results by calling the object by name. We can also use the smbinning.sumiv.plot function on the object to view them in a plot.
Code
iv_summary <-smbinning.sumiv(df = train, y ="good")
Code
iv_summary
Char IV Process
11 bureau_score 0.8310 Numeric binning OK
9 tot_rev_line 0.4989 Numeric binning OK
5 age_oldest_tr 0.2948 Numeric binning OK
3 tot_derog 0.2390 Numeric binning OK
18 ltv 0.1861 Numeric binning OK
4 tot_tr 0.1784 Numeric binning OK
10 rev_util 0.1248 Numeric binning OK
8 tot_rev_debt 0.1092 Numeric binning OK
14 down_pyt 0.0880 Numeric binning OK
16 loan_term 0.0543 Numeric binning OK
13 msrp 0.0436 Numeric binning OK
12 purch_price 0.0332 Numeric binning OK
20 used_ind 0.0195 Factor binning OK
1 bankruptcy 0.0019 Factor binning OK
15 purpose 0.0012 Factor binning OK
2 app_id NA No significant splits
6 tot_open_tr NA No significant splits
7 tot_rev_tr NA No significant splits
17 loan_amt NA No significant splits
19 tot_income NA No significant splits
21 bad NA Uniques values < 5
22 weight NA Uniques values < 5
Code
smbinning.sumiv.plot(iv_summary)
As we can see from the output above, the strong predictors of default are bureau_score, tot_rev_line, and rev_util. The moderate or medium predictors are age_oldest_tr, tot_derog, ltv, and tot_tr. These would be the variables typically used in credit modeling due to having IV scores above 0.1.
---title: "Variable Binning and Selection"format: html: code-fold: show code-tools: trueeditor: visual---# Feature CreationFeature creation and selection is one of the most important pieces to any modeling process. It is no different for credit score modeling. Before selecting the variables, we need to transform them. Specifically in credit score modeling, we need to take our continuous variables and bin them into categorical versions.# Variable GroupingScorecards end up with only just bins within a variable. There are two primary objectives when deciding on how to bin the variables:1. Eliminate weak variables or those that do not conform to good business logic.2. Group the strongest variables' attribute levels (values) in order to produce a model in the scorecard format.Binning continuous variables help simplify analysis. We no longer need to explain coefficients that imply some notion of constant effect or linearity, but instead are just comparisons of categories. This process of binning also models non-linearity in an easily interpretable way. We are not restricted to linearity of the continuous variables as some models assume. Outliers are also easily accounted for as they are typically contained within the smallest or largest bin. Lastly, missing values are no longer a problem and do not need imputation. Missing values can get their own bin making all observations available to be modeled.There are a variety of different approaches to statistically bin variables. We will focus on the two most popular ones here:1. Prebinning and Combining of Bins2. Decision / Conditional Inference TreesThe first is by prebinning the variables followed by the grouping of these bins. Imagine you had a variable whose range is from 3 to 63. This approach would first break this variable into quantile bins. Softwares typically use anywhere from 20 to 100 equally sized quantiles for this initial step. From there, we use chi-square tests to compare each adjacent pair of bins. If the bins are statistically the same with respect to the target variable using two by two contingency table Chi-square tests (Mantel-Haenzel for example), then we combine the bins. We repeat this process until no more adjacent pairs of bins can be statistically combined. Below is a visual of this process.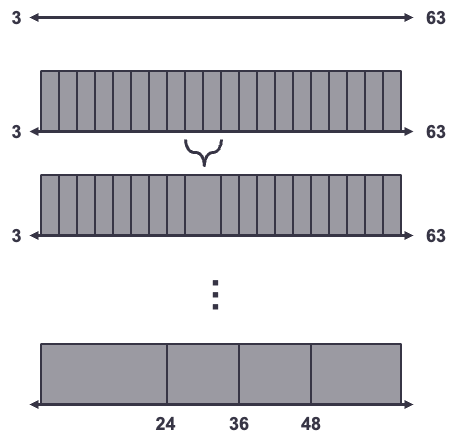{fig-align="center" width="5in"}The second common approach is through decision / conditional inference trees. The classical CART decision tree uses the Gini statistic to find the best splits for a single variable predicting the target variable. In this scenario, you have one single predictor variable as the only variable in the decision tree. Each possible split is evaluated and determined based on the Gini statistic to make the split that occurs have the highest measure of purity. This process is repeated until no further splits are possible. An example of this is show below.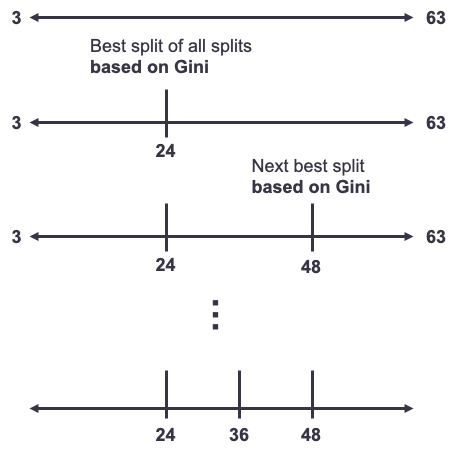{fig-align="center" width="4.77in"}Some softwares and packages use conditional inference trees instead of decision trees. These are a variation on the common CART decision tree. CART methods for decision trees potentially have inherent bias - variables with more levels are more likely to be split on if split using the Gini and entropy criterion. Conditional inference trees on the other hand add an extra step to this process. Conditional inference trees evaluate which variable is most significant first, then evaluate what is the best split of a continuous variable through the Chi-square decision tree approach on that specific variable only, not all variables. They repeat this process until no more significant places in the variable are left to be split. How does this apply to binning though? When binning a continuous variable, we are predicting the target variable using only our one continuous variable in the conditional inference tree. It evaluates if the variable is significant at predicting the target variable. If so, it finds the most significant statistical split using Chi-square tests in between each value of the continuous variable and then comparing the two groups formed by this split. After finding the most significant split you have two continuous variables - one below the split and one above. The process repeats itself until the algorithm can no longer find significant splits leading to the definition of your bins. Below is a visual of this process.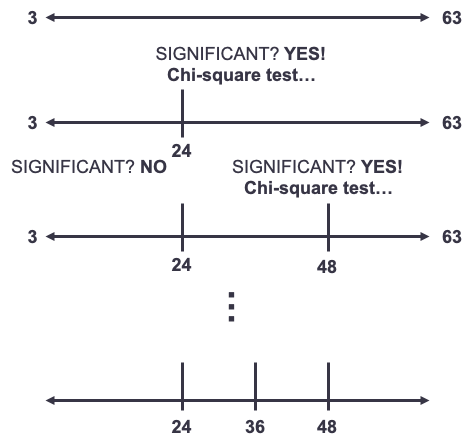{fig-align="center" width="5in"}Cut-offs (or cut points) from the decision tree algorithms might be rather rough. Sometimes we override the automatically generated cut points to more closely conform to business rules. These overrides might make the bins sub-optimal, but hopefully not too much to impact the analysis.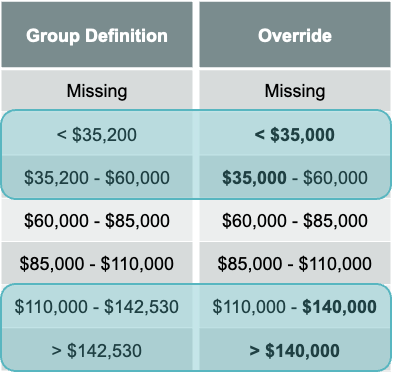{fig-align="center" width="5in"}Imagine a similar scenario for linear regression. Suppose you had two models with the first model having an $R^2 = 0.8$ and the second model having an $R^2 = 0.78$. However, the second model made more intuitive business sense than the first. You would probably choose the second model willing to sacrifice a small amount of predictive power for a model that made more intuitive sense. The same can be thought of when slightly altering the bins from these two approaches described above.Let's see how each of our softwares approaches binning continuous variables!```{r}#| include: falsesetwd("~/Dropbox/IAA/Courses/IAA/Financial Analytics/Code Files/FA-new/data/")#setwd("~/Users/ariclabarr/My Drive/Presentations/ODSC/2024 East/ODSC East Training - Credit Scoring/ODSC-Markdown/data/")accepts <-read.csv(file ="accepts.csv", header =TRUE)```::: {.panel-tabset .nav-pills}## Python```{python}#| include: false#| message: false#| error: false#| warning: falseimport pandas as pdaccepts = pd.read_csv("~/Dropbox/IAA/Courses/IAA/Financial Analytics/Code Files/FA-new/data/accepts.csv")```Before any binning is done, we need to split our data into training and testing because the binning evaluates relationships between the target variable and the predictor variables. This is easily done in Python using the `train_test_split` function from `sklearn` and the `model_selection` package. The `test_size =` option identifies the proportion of observations to be sampled and put in the test dataset. It was set as 25% of the number of rows in the dataset. The `random_state =` option specifies the seed so we can reproduce our results. Lastly, we use the `head` element of our dataframe to look at the first 5 rows.```{python}#| warning: false#| message: false#| error: falseimport pandas as pdfrom sklearn.model_selection import train_test_splittrain, test = train_test_split(accepts, test_size =0.25, random_state =1234)train.head(n =5)```Now that we have our dataset, we can start binning. The function `OptBinning` from the `optbinning` package can do either of the approaches detailed above. It also provides an additional layer of optimization on top of the approaches so it can try to maximize metrics of fit with the bins. By default, it maximizes the information value (IV) discussed in the sections below. We will look at binning the *bureau_score* variable with the *bad* target variable. The `OptBinning` function asks for the name and data type (`dtpye =` option) of the variable we are binning. Next, we use the `.fit` capabilities on our predictor and target variable (saved as `X` and `y`). The `splits` function reports the splits of the variable.```{python}#| warning: false#| message: false#| error: falseimport numpy as npfrom optbinning import OptimalBinningX = train["bureau_score"]y = train["bad"]optbin = OptimalBinning(name ="bureau_score", dtype ="numerical")optbin.fit(X, y)optbin.splits```To see more metrics about each of the splits we can use the `binning_table` function and `build()` capabilities to view the metrics. There are a lot of metrics in this table that are discussed in the next section.```{python}#| warning: false#| message: false#| error: falseiv_table = optbin.binning_tableiv_table.build()```## RFirst, to make sure that our results are comparable between software we need to import our train and test datasets from Python into R.```{r}library(reticulate)train <- py$traintest <- py$test```The R package that you choose will determine the technique that is used for the binning of the continuous variables. The `scorecard` package more closely aligns with the approach of prebinning the variable and combining the bins. The `smbinning` package as shown below uses the conditional inference tree approach.The `smbinning` function inside the `smbinning` package is the primary function to bin continuous variables. Our data set has a variable *bad* that flags when an observation has a default. However, the `smbinning` function needs a variable that defines the people in our data set that did **not** have the event - those who did not default. Below we create this new *good* variable in our training data set.```{r}train$good <-abs(train$bad -1)table(train$good)```We also need to make the categorical variables in our data set into factor variables in R so the function will not automatically assume they are numeric just because they have numerical values. We can do this with the `as.factor` function.```{r}train$bankruptcy <-as.factor(train$bankruptcy)train$used_ind <-as.factor(train$used_ind)train$purpose <-as.factor(train$purpose)```Now we are ready to bin our variables. Let's go through an example of binning the *bureau_score* variable using the `smbinning` function. The three main inputs to the `smbinning` function are the `df =` option which defines the data frame for your data, the `y =` option that defines the target variable by name, and the `x =` option that defines the predictor variable to be binned by name. To observe where the splits took place we can look at the `ivtable` or `cut` elements from our results. We will discuss all the values in the `ivtable` output in the next section.```{r}library(smbinning)result <-smbinning(df = train, y ="good", x ="bureau_score")result$ivtableresult$cuts```:::# Weight of Evidence (WOE)Weight of evidence (WOE) measures the strength of the attributes (bins) of a variable in separating events and non-events in a binary target variable. In credit scoring, that implies separating bad and good accounts respectively.Weight of evidence is based on comparing the proportion of goods to bads at each bin level and is calculated as follows for each bin within a variable:$$WOE_i = \log(\frac{Dist. Good_i}{Dist.Bad_i})$$The distribution of goods for each bin is the number of goods in that bin divided by the total number of goods across all bins. The distribution of bads for each bin is the number of bads in that bin divided by the total number of bads across all bins. An example is shown below: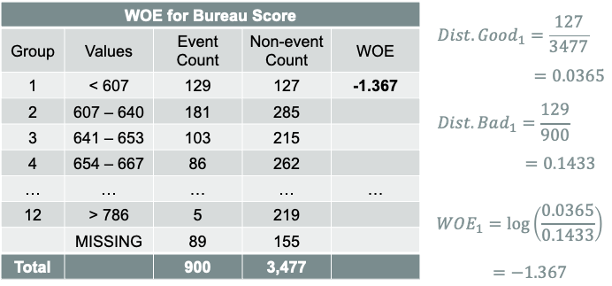{fig-align="center" width="80%"}WOE summarizes the separation between events and non-events (bads and goods) as shown in the following table: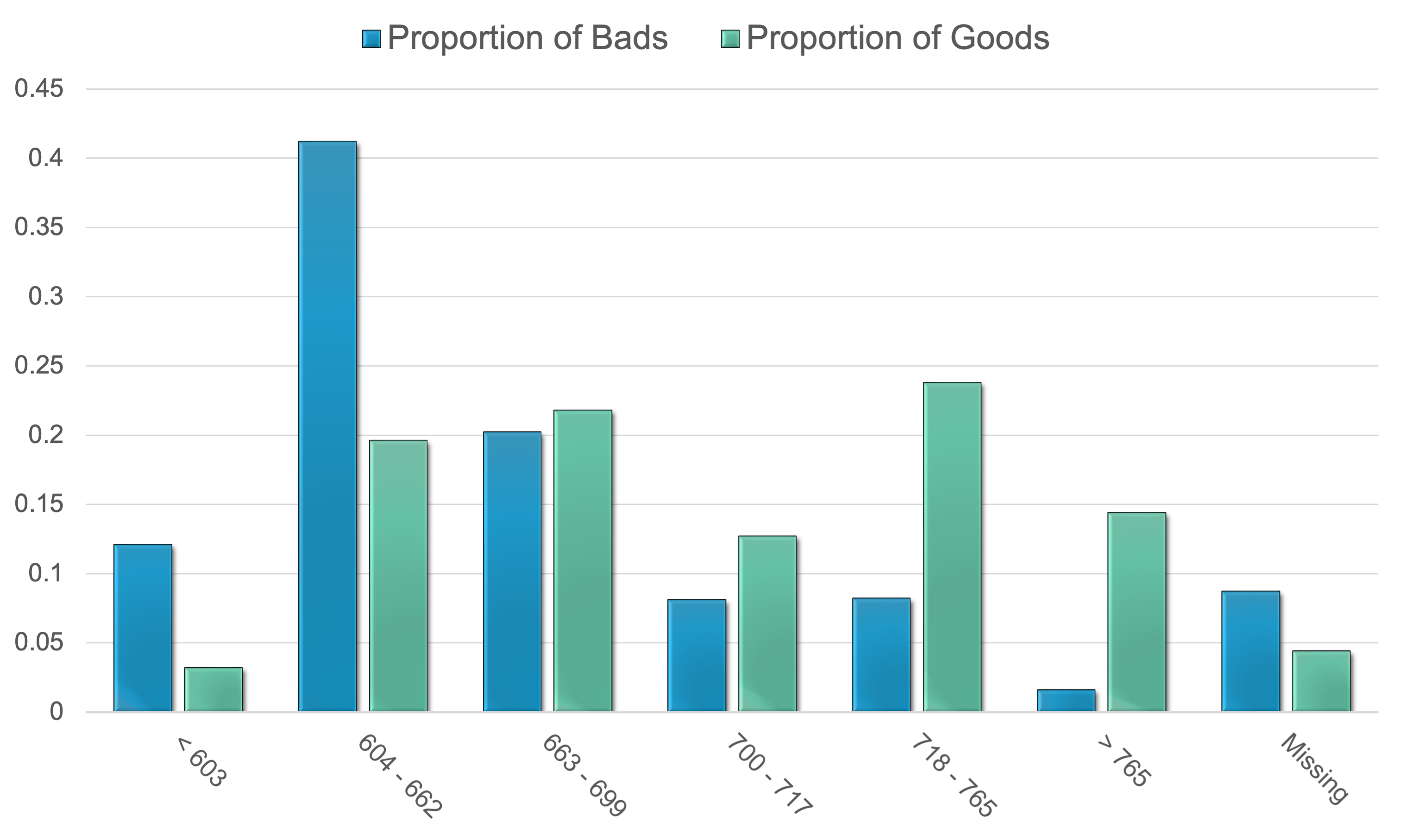{fig-align="center"}For WOE we are looking for big differences in WOE between bins.Ideally, we would like to see monotonic increases for variables that have ordered bins. This isn't always required as long as the WOE pattern in the bins makes business sense. However, if a variable's bins go back and forth between positive and negative WOE values across bins, then the variable typically has trouble separating goods and bads. Graphically, the WOE values for all the bins in the *bureau_score* variable look as follows with the line plot below:```{python}#| echo: false#| message: false#| warning: false#| error: falseiv_table.plot(metric ="woe")```The histogram in the plot above also displays the distribution of events and non-events as the WoE values are changing. WOE approximately zero implies the distribution of non-events (goods) are approximately equal to the distribution of events (bads) so that bin doesn't do a good job of separating these events and non-events. WOE of positives values implies the bin identifies observations that are non-events (goods), while WOE of negative values implies bin identifies observations that are events (bads).One quick side note. WOE values can take a value of infinity or negative infinity when quasi-complete separation exists in a category (zero events or non-events). Some people adjust the WOE calculation to include a small smoothing parameter to make the numerator or denominator of the WOE calculation not equal to zero.Let's see how to get the weight of evidence values in each of our softwares!::: {.panel-tabset .nav-pills}## PythonThe function `OptBinning` from the `optbinning` package can do either of the approaches detailed above. It also provides an additional layer of optimization on top of the approaches so it can try to maximize metrics of fit with the bins. We will look at binning the *bureau_score* variable with the *good* target variable. The `OptBinning` function asks for the name and data type (`dtpye =` option) of the variable we are binning. Next, we use the `.fit` capabilities on our predictor and target variable (saved as *x* and *y*). To see more metrics about each of the splits we can use the `binning_table` function and `build()` capabilities to view the metrics.```{python}#| message: false#| warning: false#| error: falseX = train["bureau_score"]y = train["bad"]optbin = OptimalBinning(name ="bureau_score", dtype ="numerical")optbin.fit(X, y)iv_table = optbin.binning_tableiv_table.build()```The weight of evidence values are listed in the WoE column and follow a similar calculation although we used different bin values for the hand calculation above. We can easily get the plot of the WOE values using the `.plot` function with the `metric = "woe"` option. The resulting plot is the same as the WOE plot above.```{python}#| message: false#| warning: false#| error: falseiv_table.plot(metric ="woe")```You can get weight of evidence values for a factor variable as well without needing to rebin the values. This is done using the `OptBinning` function on the *purpose* variable as shown below, now with a `dtype =` option set to categorical:```{python}#| message: false#| warning: false#| error: falseX = train["purpose"]y = train["bad"]optbin = OptimalBinning(name ="purpose", dtype ="categorical")optbin.fit(X, y)iv_table = optbin.binning_tableiv_table.build()```## RThe `smbinning` function inside the `smbinning` package is the primary function to bin continuous variables. Let's go through an example of binning the *bureau_score* variable using the `smbinning` function. The three main inputs to the `smbinning` function are the `df =` option which defines the data frame for your data, the `y =` option that defines the target variable by name, and the `x =` option that defines the predictor variable to be binned by name.As we previously saw, the `ivtable` element contains a summary of the splits as well as some information regarding each split including weight of evidence.```{r}#| message: false#| warning: false#| error: falseresult <-smbinning(df = train, y ="good", x ="bureau_score")result$ivtable```The weight of evidence values are listed in the WoE column and the same values as shown above. We can easily get the plot of the WOE values using the `smbinning.plot` function with the `option = "WoE"` option.```{r}#| message: false#| warning: false#| error: falsesmbinning.plot(result,option="WoE",sub="Bureau Score")```You can get weight of evidence values for a factor variable as well without needing to rebin the values. This is done using the `smbinning.factor` function on the *purpose* variable as shown below:```{r}#| message: false#| warning: false#| error: falseresult <-smbinning.factor(df = train, y ="good", x ="purpose")result$ivtable```:::# Information Value (IV) & Variable SelectionWeight of evidence summarizes the individual categories or bins of a variable. However, we need a measure of how well all the categories in a variable do at separating the events from non-events. That is what information value (IV) is for. IV uses the WOE from each category as a piece of its calculation:$$IV = \sum_{i=1}^L (Dist.Good_i - Dist.Bad_i)\times \log(\frac{Dist.Good}{Dist.Bad})$$In credit modeling, IV is used in some instances to actually select which variables belong in the model. Here are some typical IV ranges for determining the strength of a predictor variable at predicting the target variable:- $0 \le IV < 0.02$ - Not predictor- $0.02 \le IV < 0.1$ - Weak predictor- $0.1 \le IV < 0.25$ - Moderate (medium) predictor- $0.25 \le IV$ - Strong predictorVariables with information values greater than 0.1 are typically used in credit modeling.Some resources will say that IV values greater than 0.5 might signal over-predicting of the target. In other words, maybe the variable is too strong of a predictor because of how that variable was originally constructed. For example, if all previous loan decisions have been made only on bureau score, then of course that variable would be highly predictive and possibly the only significant variable. In these situations, good practice is to build one model with only bureau score and another model without bureau score but with other important factors. We then ensemble these models together.Let's see how to get the information values for our variables in each of our softwares!::: {.panel-tabset .nav-pills}## PythonThe function `OptBinning` from the `optbinning` package can do either of the approaches detailed above. It also provides an additional layer of optimization on top of the approaches so it can try to maximize metrics of fit with the bins. We will look at binning the *bureau_score* variable with the *good* target variable. The `OptBinning` function asks for the name and data type (`dtpye =` option) of the variable we are binning. Next, we use the `.fit` capabilities on our predictor and target variable (saved as `X` and `y`). To see more metrics about each of the splits we can use the `binning_table` function and `build()` capabilities to view the metrics.As we previously saw, the `binning_table` element contains a summary of the splits as well as some information regarding each split including information value.```{python}#| warning: false#| error: false#| message: falseX = train["bureau_score"]y = train["bad"]optbin = OptimalBinning(name ="bureau_score", dtype ="numerical")optbin.fit(X, y)iv_table = optbin.binning_tableiv_table.build()```The information value is listed in the IV column. The IV numbers in each of the rows for the bins is the component of the IV from each of the categories. The final row is the sum of the previous rows which is the overall variable IV.Another way to view the information value for every variable in the dataset is to use the `BinningProcess` function. The main input to this function is the list of column names you want evaluated. We have training data selected without the target variable, *bad*, or the weighting variable, *weight*. The `categorical_variables =` option is used to specify which variables in the data are categorical instead of continuous. We can also use the `selection_criteria` option to define what variables we would want to include in a follow-up model. Here, we are only choosing the variables with IV values above 0.1. We then use the same `.fit` format where you define the variables with the `X` object and the `y` object to define the target variable. The function then calculates the IV for each variable in the dataset with the target variable.To view these information values for each variable we can just print out a table of the results by calling the `summary` object. Here we just print out the splits with the IV values instead of all the summary statistics.```{python}#| warning: false#| error: false#| message: falsefrom optbinning import BinningProcesscolnames =list(train.columns[0:20])X = train[colnames]selection_criteria = {"iv": {"min": 0.1, "max": 1}}bin_proc = BinningProcess(colnames, selection_criteria = selection_criteria, categorical_variables = ["bankruptcy", "purpose", "used_ind"])iv_all = bin_proc.fit(X, y).summary()iv_all[iv_all.columns[0:6]].sort_values(by = ["iv"], ascending =False)```As we can see from the output above, the strong predictors of default are *bureau_score*, *tot_rev_line*, *rev_util*, and *age_oldest_tr*. The moderate or medium predictors are *tot_derog*, *ltv*, *tot_tr, tot_rev_debt*, *down_pyt*, *tot_income*, and *tot_rev_tr*. These would be the variables typically used in credit modeling due to having IV scores above 0.1.## RThe `smbinning` function inside the `smbinning` package is the primary function to bin continuous variables. Let's go through an example of binning the *bureau_score* variable using the `smbinning` function. The three main inputs to the `smbinning` function are the `df =` option which defines the data frame for your data, the `y =` option that defines the target variable by name, and the `x =` option that defines the predictor variable to be binned by name.As we previously saw, the `ivtable` element contains a summary of the splits as well as some information regarding each split including information value.```{r}#| message: false#| error: false#| warning: falseresult <-smbinning(df = train, y ="good", x ="bureau_score")result$ivtable```The information value is listed in the IV column and the last row. The IV numbers in each of the rows for the bins is the component of the IV from each of the categories. The final row is the sum of the previous rows which is the overall variable IV.Another way to view the information value for every variable in the dataset is to use the `smbinning.sumiv` function. The only two inputs to this function are the `data =` option where you define the dataset and the `y =` option to define the target variable. The function then calculates the IV for each variable in the dataset with the target variable.To view these information values for each variable we can just print out a table of the results by calling the object by name. We can also use the `smbinning.sumiv.plot` function on the object to view them in a plot.```{r}#| message: false#| warning: false#| error: false#| eval: falseiv_summary <-smbinning.sumiv(df = train, y ="good")``````{r}#| message: false#| warning: false#| error: false#| include: falseiv_summary <-smbinning.sumiv(df = train, y ="good")``````{r}#| message: false#| warning: false#| error: falseiv_summarysmbinning.sumiv.plot(iv_summary)```As we can see from the output above, the strong predictors of default are *bureau_score*, *tot_rev_line*, and *rev_util*. The moderate or medium predictors are *age_oldest_tr*, *tot_derog*, *ltv*, and *tot_tr*. These would be the variables typically used in credit modeling due to having IV scores above 0.1.:::