Now that we have transformed our variables for modeling, we can start with the process of building our model. In building credit models, we first build an initial credit scoring model. In each of the models that we build we must take the following three steps:
Build the model
Evaluate the model
Convert the model to a scorecard
The scorecard is typically based on a logistic regression model:
In the above equation, \(p\) is the probability of default given the inputs in the model. However, instead of using the original variables for the model, credit scoring models and their complimenting scorecards are based on binned variables as their foundation.
Instead of using the original variables for the model, scorecard models have the binned variables as their foundation. There are two different approaches to handling this:
WoE approach - use the WOE scores as new continuous variables
Binned approach - use binned variables as new variables
These two approaches can be best seen by looking at some observations from our dataset as seen below:
There are advantages and disadvantages of both techniques.
For the WoE approach, all of the variables are treated as continuous which reduces the size of the model. All of these variables are now on the same WoE scale which makes the variables comparable in terms of their variable importance (the logistic regression coefficients here). This is the default approach in Python’s OptBinning package detailed below.
For the binned approach, the variables are all now categorical in nature. That means that we have many more variables since they have to be coded (one-hot encoding for example) to get them into the model. However, this approach is the programmed approach in R which makes the implementation much easier in that software.
As we saw previously, another way to view the information value for every variable in the dataset is to use the BinningProcess function. The main input to this function is the list of column names you want evaluated. We have training data selected without the target variable, bad, or the weighting variable, weight. The categorical_variables = option is used to specify which variables in the data are categorical instead of continuous. We can also use the selection_criteria option to define what variables we would want to include in a follow-up model. Here, we are only choosing the variables with IV values above 0.1. We then use the same .fit format where you define the variables with the X object and the y object to define the target variable. The function then calculates the IV for each variable in the dataset with the target variable. It also serves as an input to the Scorecard function that will build our model.
After the BinningProcess object, we set the estimator (the model itself) to the LogisticRegression function from sklearn.linear_model. The BinningProcess object will create the WoE input variables to be put into the LogisticRegression model.
Both the BinningProcess and LogisticRegression serve as inputs to the Scorecard function. The other inputs to the Scorecard function define how you want to create the scorecard points. We are using the pdo_odds approach which is detailed further in the next section.
After that we use the .fit framework as we have done previously to build our model. The sample_weight option corrects the model for the oversampling of the defaulters that was used in the creation of the dataset.
Code
import numpy as npimport pandas as pdfrom sklearn.linear_model import LogisticRegressionfrom optbinning import BinningProcess
(CVXPY) Dec 19 04:35:55 PM: Encountered unexpected exception importing solver GLOP:
RuntimeError('Unrecognized new version of ortools (9.11.4210). Expected < 9.10.0. Please open a feature request on cvxpy to enable support for this version.')
(CVXPY) Dec 19 04:35:55 PM: Encountered unexpected exception importing solver PDLP:
RuntimeError('Unrecognized new version of ortools (9.11.4210). Expected < 9.10.0. Please open a feature request on cvxpy to enable support for this version.')
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
To view the actual coefficients from the logistic regression for each of the variables we can use the .table(style = "detailed") function on the Scorecard object.
The smbinning.gen function will create binned, factor variables in R based on the results from the smbinning function. The df = option defines the dataset. The ivout = option defines the specific results for the variable of interest as you can only do this function one variable at a time. The chrname = function defines the names of the new binned variable in your dataset. Instead of looping through the variables in the dataset, we are going through one at a time to see what the function is doing.
Code
library(smbinning)smb_bureau_score <-smbinning(df = train, y ="good", x ="bureau_score")smb_tot_rev_line <-smbinning(df = train, y ="good", x ="tot_rev_line")smb_rev_util <-smbinning(df = train, y ="good", x ="rev_util")smb_age_oldest_tr <-smbinning(df = train, y ="good", x ="age_oldest_tr")smb_tot_derog <-smbinning(df = train, y ="good", x ="tot_derog")smb_ltv <-smbinning(df = train, y ="good", x ="ltv")smb_tot_tr <-smbinning(df = train, y ="good", x ="tot_tr")train <-smbinning.gen(df = train, ivout = smb_bureau_score, chrname ="bureau_score_bin")train <-smbinning.gen(df = train, ivout = smb_tot_rev_line, chrname ="tot_rev_line_bin")train <-smbinning.gen(df = train, ivout = smb_rev_util, chrname ="rev_util_bin")train <-smbinning.gen(df = train, ivout = smb_age_oldest_tr, chrname ="age_oldest_tr_bin")train <-smbinning.gen(df = train, ivout = smb_tot_derog, chrname ="tot_derog_bin")train <-smbinning.gen(df = train, ivout = smb_ltv, chrname ="ltv_bin")train <-smbinning.gen(df = train, ivout = smb_tot_tr, chrname ="tot_tr_bin")head(train, n =5)
As we can see above, we now have a dataset with extra columns at the end representing the binned versions of our variables.
With these variables now created, we can add them to the logistic regression in R. The glm function in R will provide us the ability to model binary logistic regressions. Similar to most modeling functions in R, you can specify a model formula. The family = binomial(link = "logit") option is there to specify that we are building a logistic model. Generalized Linear models (GLM) are a general class of models where logistic regression is a special case where the link function is the logit function. The weights = option corrects the model for the oversampling of the defaulters that was used in the creation of the dataset.
Use the summary function to look at the necessary output. We will not show it here to save output space due to all of the variables and their categories in our model.
Code
summary(initial_score)
Now that we have our logistic credit scoring model built we can evaluate them before adding on the scorecard points.
Model Evaluation
Credit models are evaluated as most classification models. Overall model performance is typically evaluated on area under the ROC curve as well as the K-S statistic.
Luckily, the optbinning package has great functionality for evaluating model performance. The plot_auc_roc and plot_ks functions provides many summary statistics and plots to evaluate our models. First, we must get the predictions from our model by creating a new variable y_pred in our dataset from the predict_proba element of our Scorecard model object. We want the second column (denoted with a [:, 1] so we can get the probability of a 1 (a good). This new y_pred variable is one of the inputs of the evaluation functions.
First we will plot the ROC curve using the plot_auc_roc function. The only inputs are the target variable and the predicted probabilities we just calculated.
Code
from matplotlib import pyplot as pltfrom optbinning.scorecard import plot_auc_roc, plot_ksy_pred = scorecard.predict_proba(X)[:, 1]plot_auc_roc(y, y_pred)plt.show()
Next we use the same inputs but change the function to the plot_ks function to the KS plot.
Code
plot_ks(y, y_pred)plt.show()
From the plot above we see both the value of the KS statistic as well as the optimal cut-off from the probabilities of the model based on the Youden J statistic. From the plot above, a predicted probability above 0.06 would be flagged as a defaulter. In the next section we will see how to apply scores to these probabilities.
Luckily, the smbinning package has great functionality for evaluating model performance. The smbinning.metrics function provides many summary statistics and plots to evaluate our models. First, we must get the predictions from our model by creating a new variable pred in our dataset from the fitted.values element of our glm model object. This new pred variable is one of the inputs of the smbinning.metrics function. The dataset = option defines our dataset. The prediction = option is where we define the variable in the dataset with the predictions from our model. The actualclass = option defines the target variable from our dataset. The report = 1 option prints out a report with a variety of summary statistics as shown below:
The report provides multiple pieces of model evaluation. At the top it provides the KS and AUC metrics for the model. Next, the report summarizes metrics from the classification matrix. At the top of this section it provides the optimal cut-off level based on the Youden J statistic. At this cut-off it provides the number of true positives, false positives, true negatives, false negatives, total positives, and total negatives. The last section of the report provides many business performance metrics such as sensitivity, specificity, precision, and many more as seen above.
By using the plot = option in the smbinning.metrics function you can plot either the KS plot or ROC curve.
From the plot above we see both the value of the KS statistic as well as the optimal cut-off from the probabilities of the model based on the Youden J statistic. From the plot above, a predicted probability above 0.93 would be flagged as a non-defaulter. In the next section we will see how to apply scores to these probabilities.
Just in case you were curious how the traditional approach to developing variables using WOE values would have performed instead of the “modern” approach of using the binned variables, here is a comparison:
As you can see, they are very similar in their performance.
Scaling the Scorecard
The last step of the credit modeling process is building the scorecard itself. To create the scorecard we need to relate the predicted odds from our logistic regression model to the scorecard. The relationship between the odds and scores is represented by a linear function:
\[
Score = Offset + Factor \times \log(odds)
\]
All that we need to define is the amount of points to double the odds (called PDO) and the corresponding scorecard points. From there we have the following extra equation:
Through some basic algebra, the solution to the \(Factor\) and \(Offset\) is shown to be:
\[
Factor = \frac{PDO}{\log(2)}
\]
\[
Offset = Score - Factor \times \log(odds)
\]
For example, if a scorecard were scaled where the developer wanted odds of 50:1 at 600 points and wanted the PDO = 20. Through the above equations we calculate \(Factor = 28.85\) and \(Offset = 487.12\). Therefore, the corresponding score for each predicted odds from the logistic regression model is calculated as:
\[
Score = 487.12 + 28.85\times \log(odds)
\]
For this example, we would then calculate the score for each individual in our dataset. Notice how the above equation has the \(\log(odds)\) which is the prediction from a logistic regression model \(\log(odds) = \hat{\beta}_0 + \hat{\beta}_1 x_1 \cdots\). This is one of the reasons logistic regression is still very popular in the credit modeling world.
The next step in the scorecard is to allocate the scorecard points to each of the categories (bins) in each of the variables. The points that are allocated to the \(i^{th}\) bin of variable \(j\) are computed as follows:
The \(WOE_{i,j}\) is the weight of evidence of the \(i^{th}\) bin of variable \(j\). The coefficient of the variable \(j\), \(\hat{\beta}_j\), as well as the intercept \(\hat{\beta}_0\), come from the logistic regression model. \(L\) is the number of variables in the model.
Now that we have our scorecard, we can use those options we previous talked about in the Scorecard function to define the pdo, odds, and scorecard_points to help define our scorecard. Now all we have to do is use the table function on our Scorecard object with a style = "summary" option to get the points for each category of each variable.
Now that we have our model, we can use the smbinning.scaling function to help create our scores. The input to this function are the model object first, here initial_score, followed by the pdo, score, and odds options similar to what we defined above. We will use the same values as we did above for each of these.
Next, we use the smbinning.scoring.gen function to take these scaling calculations from the smbinning.scaling function and create a dataset with our scores. The only inputs for this function are the object from our smbinning.scaling function and our dataset.
Looking at the last few columns from our newly created dataset, we have a points column for each variable in our model along with a final Score variable that contains the final scorecard score for each observation.
Looking at the histogram below we see that our good customers tend to have higher scores than our bad customers. The vertical dashed lines represent the average score for each group. This is exactly what we are looking for!
This initial credit scoring model based only on the applicants who got loans (accepted applicants) is called a behavioral scorecard because it models the behavior of your current loans.
---title: "Building Scorecard"format: html: code-fold: show code-tools: trueeditor: visual---```{python}#| include: false#| message: false#| error: false#| warning: falseimport pandas as pdaccepts = pd.read_csv("~/Dropbox/IAA/Courses/IAA/Financial Analytics/Code Files/FA-new/data/accepts.csv")from sklearn.model_selection import train_test_splittrain, test = train_test_split(accepts, test_size =0.25, random_state =1234)``````{r}#| include: false#| message: false#| error: false#| warning: falselibrary(reticulate)train <- py$traintest <- py$testtrain$good <-abs(train$bad -1)train$bankruptcy <-as.factor(train$bankruptcy)train$used_ind <-as.factor(train$used_ind)train$purpose <-as.factor(train$purpose)```# Logistic Regression ExampleNow that we have transformed our variables for modeling, we can start with the process of building our model. In building credit models, we first build an initial credit scoring model. In each of the models that we build we must take the following three steps:1. Build the model2. Evaluate the model3. Convert the model to a scorecardThe scorecard is typically based on a logistic regression model:$$logit(p) = \log(\frac{p}{1-p}) = \beta_0 + \beta_1 x_1 + \cdots + \beta_k x_k$$In the above equation, $p$ is the probability of default given the inputs in the model. However, instead of using the original variables for the model, credit scoring models and their complimenting scorecards are based on binned variables as their foundation.Instead of using the original variables for the model, scorecard models have the binned variables as their foundation. There are two different approaches to handling this:1. WoE approach - use the WOE scores as new continuous variables2. Binned approach - use binned variables as new variablesThese two approaches can be best seen by looking at some observations from our dataset as seen below: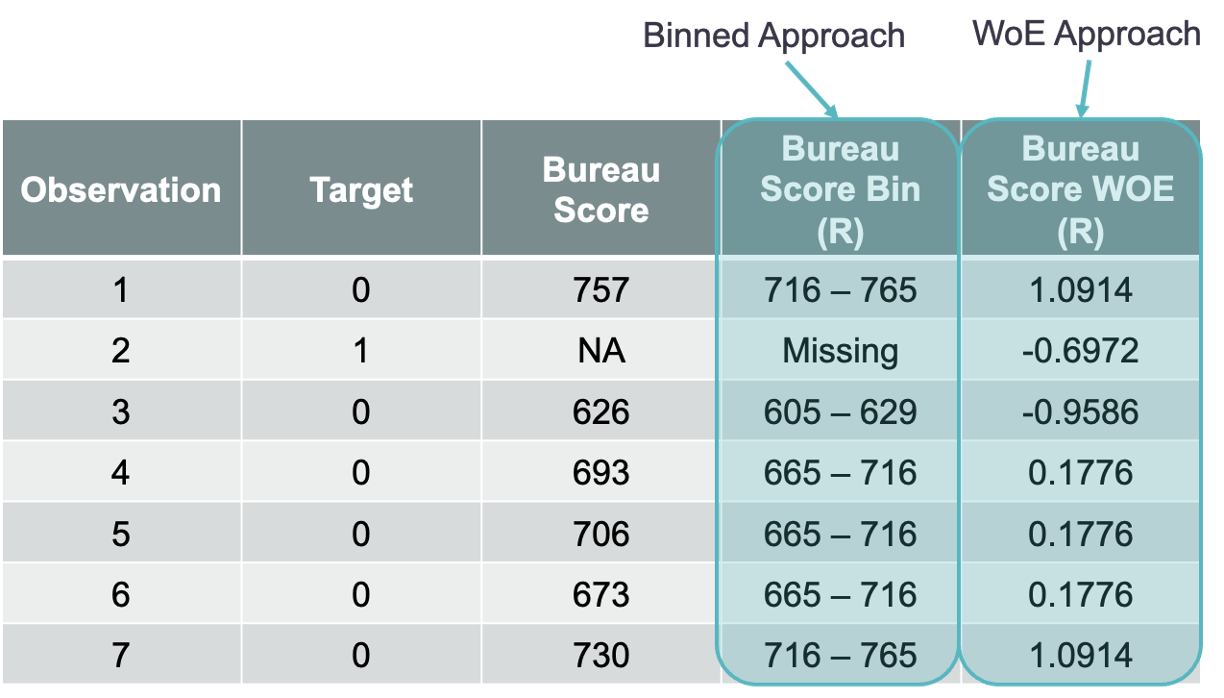{fig-align="center" width="80%"}There are advantages and disadvantages of both techniques.For the WoE approach, all of the variables are treated as continuous which reduces the size of the model. All of these variables are now on the same WoE scale which makes the variables comparable in terms of their variable importance (the logistic regression coefficients here). This is the default approach in Python's `OptBinning` package detailed below.For the binned approach, the variables are all now categorical in nature. That means that we have many more variables since they have to be coded (one-hot encoding for example) to get them into the model. However, this approach is the programmed approach in R which makes the implementation much easier in that software.::: {.panel-tabset .nav-pills}## PythonAs we saw previously, another way to view the information value for every variable in the dataset is to use the `BinningProcess` function. The main input to this function is the list of column names you want evaluated. We have training data selected without the target variable, *bad*, or the weighting variable, *weight*. The `categorical_variables =` option is used to specify which variables in the data are categorical instead of continuous. We can also use the `selection_criteria` option to define what variables we would want to include in a follow-up model. Here, we are only choosing the variables with IV values above 0.1. We then use the same `.fit` format where you define the variables with the `X` object and the `y` object to define the target variable. The function then calculates the IV for each variable in the dataset with the target variable. It also serves as an input to the `Scorecard` function that will build our model.After the `BinningProcess` object, we set the estimator (the model itself) to the `LogisticRegression` function from `sklearn.linear_model`. The `BinningProcess` object will create the WoE input variables to be put into the `LogisticRegression` model.Both the `BinningProcess` and `LogisticRegression` serve as inputs to the `Scorecard` function. The other inputs to the `Scorecard` function define how you want to create the scorecard points. We are using the `pdo_odds` approach which is detailed further in the next section.After that we use the `.fit` framework as we have done previously to build our model. The `sample_weight` option corrects the model for the oversampling of the defaulters that was used in the creation of the dataset.```{python}#| message: false#| error: false#| warning: falseimport numpy as npimport pandas as pdfrom sklearn.linear_model import LogisticRegressionfrom optbinning import BinningProcessfrom optbinning import Scorecardcolnames =list(train.columns[0:20])X = train[colnames]y = train["bad"]selection_criteria = {"iv": {"min": 0.1, "max": 1}}bin_proc = BinningProcess(colnames, selection_criteria = selection_criteria, categorical_variables = ["bankruptcy", "purpose", "used_ind"])estimator = LogisticRegression(solver ="lbfgs")scorecard = Scorecard(binning_process = bin_proc, estimator = estimator, scaling_method ="pdo_odds", scaling_method_params = {"pdo": 20, "scorecard_points": 600, "odds": 50})scorecard.fit(X, y, sample_weight = train["weight"])```To view the actual coefficients from the logistic regression for each of the variables we can use the `.table(style = "detailed")` function on the `Scorecard` object.```{python}#| message: false#| error: false#| warning: falsescorecard.table(style ="detailed")```## RThe `smbinning.gen` function will create binned, factor variables in R based on the results from the `smbinning` function. The `df =` option defines the dataset. The `ivout =` option defines the specific results for the variable of interest as you can only do this function one variable at a time. The `chrname =` function defines the names of the new binned variable in your dataset. Instead of looping through the variables in the dataset, we are going through one at a time to see what the function is doing.```{r}#| message: false#| error: false#| warning: falselibrary(smbinning)smb_bureau_score <-smbinning(df = train, y ="good", x ="bureau_score")smb_tot_rev_line <-smbinning(df = train, y ="good", x ="tot_rev_line")smb_rev_util <-smbinning(df = train, y ="good", x ="rev_util")smb_age_oldest_tr <-smbinning(df = train, y ="good", x ="age_oldest_tr")smb_tot_derog <-smbinning(df = train, y ="good", x ="tot_derog")smb_ltv <-smbinning(df = train, y ="good", x ="ltv")smb_tot_tr <-smbinning(df = train, y ="good", x ="tot_tr")train <-smbinning.gen(df = train, ivout = smb_bureau_score, chrname ="bureau_score_bin")train <-smbinning.gen(df = train, ivout = smb_tot_rev_line, chrname ="tot_rev_line_bin")train <-smbinning.gen(df = train, ivout = smb_rev_util, chrname ="rev_util_bin")train <-smbinning.gen(df = train, ivout = smb_age_oldest_tr, chrname ="age_oldest_tr_bin")train <-smbinning.gen(df = train, ivout = smb_tot_derog, chrname ="tot_derog_bin")train <-smbinning.gen(df = train, ivout = smb_ltv, chrname ="ltv_bin")train <-smbinning.gen(df = train, ivout = smb_tot_tr, chrname ="tot_tr_bin")head(train, n =5)```As we can see above, we now have a dataset with extra columns at the end representing the binned versions of our variables.With these variables now created, we can add them to the logistic regression in R. The `glm` function in R will provide us the ability to model binary logistic regressions. Similar to most modeling functions in R, you can specify a model formula. The `family = binomial(link = "logit")` option is there to specify that we are building a logistic model. Generalized Linear models (GLM) are a general class of models where logistic regression is a special case where the link function is the logit function. The `weights =` option corrects the model for the oversampling of the defaulters that was used in the creation of the dataset.```{r}#| message: false#| error: false#| warning: falseinitial_score <-glm(data = train, good ~ bureau_score_bin + tot_rev_line_bin + rev_util_bin + age_oldest_tr_bin + tot_derog_bin + ltv_bin#tot_tr_bin , weights = train$weight, family =binomial(link ="logit"))```Use the `summary` function to look at the necessary output. We will not show it here to save output space due to all of the variables and their categories in our model.```{r}#| message: false#| error: false#| warning: false#| eval: falsesummary(initial_score)```:::Now that we have our logistic credit scoring model built we can evaluate them before adding on the scorecard points.# Model EvaluationCredit models are evaluated as most classification models. Overall model performance is typically evaluated on area under the ROC curve as well as the K-S statistic.Let's see how to perform this in our software!::: {.panel-tabset .nav-pills}## PythonLuckily, the `optbinning` package has great functionality for evaluating model performance. The `plot_auc_roc` and `plot_ks` functions provides many summary statistics and plots to evaluate our models. First, we must get the predictions from our model by creating a new variable *y_pred* in our dataset from the `predict_proba` element of our `Scorecard` model object. We want the second column (denoted with a `[:, 1]` so we can get the probability of a 1 (a good). This new *y_pred* variable is one of the inputs of the evaluation functions.First we will plot the ROC curve using the `plot_auc_roc` function. The only inputs are the target variable and the predicted probabilities we just calculated.```{python}#| message: false#| error: false#| warning: falsefrom matplotlib import pyplot as pltfrom optbinning.scorecard import plot_auc_roc, plot_ksy_pred = scorecard.predict_proba(X)[:, 1]plot_auc_roc(y, y_pred)plt.show()```Next we use the same inputs but change the function to the `plot_ks` function to the KS plot.```{python}#| message: false#| error: false#| warning: falseplot_ks(y, y_pred)plt.show()```From the plot above we see both the value of the KS statistic as well as the optimal cut-off from the probabilities of the model based on the Youden J statistic. From the plot above, a predicted probability above 0.06 would be flagged as a defaulter. In the next section we will see how to apply scores to these probabilities.## RLuckily, the `smbinning` package has great functionality for evaluating model performance. The `smbinning.metrics` function provides many summary statistics and plots to evaluate our models. First, we must get the predictions from our model by creating a new variable *pred* in our dataset from the `fitted.values` element of our `glm` model object. This new *pred* variable is one of the inputs of the `smbinning.metrics` function. The `dataset =` option defines our dataset. The `prediction =` option is where we define the variable in the dataset with the predictions from our model. The `actualclass =` option defines the target variable from our dataset. The `report = 1` option prints out a report with a variety of summary statistics as shown below:```{r}#| message: false#| error: false#| warning: falsetrain$pred <- initial_score$fitted.valuessmbinning.metrics(dataset = train, prediction ="pred", actualclass ="good", report =1)```The report provides multiple pieces of model evaluation. At the top it provides the KS and AUC metrics for the model. Next, the report summarizes metrics from the classification matrix. At the top of this section it provides the optimal cut-off level based on the Youden J statistic. At this cut-off it provides the number of true positives, false positives, true negatives, false negatives, total positives, and total negatives. The last section of the report provides many business performance metrics such as sensitivity, specificity, precision, and many more as seen above.By using the `plot =` option in the `smbinning.metrics` function you can plot either the KS plot or ROC curve.```{r}#| message: false#| error: false#| warning: falsesmbinning.metrics(dataset = train, prediction ="pred", actualclass ="good", report =0, plot ="ks")smbinning.metrics(dataset = train, prediction ="pred", actualclass ="good", report =0, plot ="auc")```From the plot above we see both the value of the KS statistic as well as the optimal cut-off from the probabilities of the model based on the Youden J statistic. From the plot above, a predicted probability above 0.93 would be flagged as a non-defaulter. In the next section we will see how to apply scores to these probabilities.:::Just in case you were curious how the traditional approach to developing variables using WOE values would have performed instead of the "modern" approach of using the binned variables, here is a comparison:{fig-align="center" width="80%"}As you can see, they are very similar in their performance.# Scaling the ScorecardThe last step of the credit modeling process is building the scorecard itself. To create the scorecard we need to relate the predicted odds from our logistic regression model to the scorecard. The relationship between the odds and scores is represented by a linear function:$$Score = Offset + Factor \times \log(odds)$$All that we need to define is the amount of points to double the odds (called PDO) and the corresponding scorecard points. From there we have the following extra equation:$$Score + PDO = Offset + Factor \times \log(2 \times odds)$$Through some basic algebra, the solution to the $Factor$ and $Offset$ is shown to be:$$Factor = \frac{PDO}{\log(2)}$$$$Offset = Score - Factor \times \log(odds)$$For example, if a scorecard were scaled where the developer wanted odds of 50:1 at 600 points and wanted the PDO = 20. Through the above equations we calculate $Factor = 28.85$ and $Offset = 487.12$. Therefore, the corresponding score for each predicted odds from the logistic regression model is calculated as:$$Score = 487.12 + 28.85\times \log(odds)$$For this example, we would then calculate the score for each individual in our dataset. Notice how the above equation has the $\log(odds)$ which is the prediction from a logistic regression model $\log(odds) = \hat{\beta}_0 + \hat{\beta}_1 x_1 \cdots$. This is one of the reasons logistic regression is still very popular in the credit modeling world.The next step in the scorecard is to allocate the scorecard points to each of the categories (bins) in each of the variables. The points that are allocated to the $i^{th}$ bin of variable $j$ are computed as follows:$$Points_{i,j} = -(WOE_{i,j} \times \hat{\beta}_j + \frac{\hat{\beta}_0}{L}) \times Factor + \frac{Offset}{L}$$The $WOE_{i,j}$ is the weight of evidence of the $i^{th}$ bin of variable $j$. The coefficient of the variable $j$, $\hat{\beta}_j$, as well as the intercept $\hat{\beta}_0$, come from the logistic regression model. $L$ is the number of variables in the model.Let's see this in our software!::: {.panel-tabset .nav-pills}## PythonNow that we have our scorecard, we can use those options we previous talked about in the `Scorecard` function to define the `pdo`, `odds`, and `scorecard_points` to help define our scorecard. Now all we have to do is use the `table` function on our `Scorecard` object with a `style = "summary"` option to get the points for each category of each variable.```{python}#| message: false#| error: false#| warning: falsescorecard.table(style ="summary")```## RNow that we have our model, we can use the `smbinning.scaling` function to help create our scores. The input to this function are the model object first, here *initial_score*, followed by the `pdo`, `score`, and `odds` options similar to what we defined above. We will use the same values as we did above for each of these.Next, we use the `smbinning.scoring.gen` function to take these scaling calculations from the `smbinning.scaling` function and create a dataset with our scores. The only inputs for this function are the object from our `smbinning.scaling` function and our dataset.```{r}#| message: false#| error: false#| warning: falsebin_model <-smbinning.scaling(initial_score, pdo =20, score =600, odds =50)train_bin <-smbinning.scoring.gen(bin_model, dataset = train)head(train_bin[,32:38], n =5)```Looking at the last few columns from our newly created dataset, we have a points column for each variable in our model along with a final *Score* variable that contains the final scorecard score for each observation.:::Looking at the histogram below we see that our good customers tend to have higher scores than our bad customers. The vertical dashed lines represent the average score for each group. This is exactly what we are looking for!```{python}#| message: false#| warning: false#| error: false#| echo: falsescore = scorecard.score(X)mask = y ==0plt.hist(score[mask], label="Non-defaulters", color="b", alpha=0.35)plt.hist(score[~mask], label="Defaulters", color="r", alpha=0.35)plt.xlabel("score")plt.legend()plt.show()```This initial credit scoring model based **only** on the applicants who got loans (accepted applicants) is called a **behavioral scorecard** because it models the behavior of your current loans.