Generalized Additive Models (GAM’s) provide a general framework for adding of non-linear functions together instead of the typical linear structure of linear regression. GAM’s can be used for either continuous or categorical target variables. The structure of GAM’s are the following:
The \(f_i(x_i)\) functions are complex, nonlinear functions on the predictor variables. GAM’s add these complex, yet individual functions together. This allows for many complex relationships to try and model with to potentially predict your target variable better. We will examine a few different forms of GAM’s below.
Piecewise Linear Regression
The slope of the linear relationship between a predictor variable and a target variable can change over different values of the predictor variable. The typical straight-line model \(\hat{y} = \beta_0 + \beta_1x_1\) will not be a good fit for this type of data.
Here is an example of a data set that exhibits this behavior - comprehensive strength of concrete and the proportion of water mixed with cement. The comprehensive strength decreases at a much faster rate for batches with a greater than 70% water/cement ratio.
Linear Regression
Piecewise Linear Regression
If you were to fit a linear regression as the first image above, it wouldn’t represent the data very well. However, this is perfect for a piecewise linear regression. Piecewise linear regression is a model where there are different straight-line relationships for different intervals in the predictor variable. The following piecewise linear regression is for two slopes:
The \(k\) value in the equation above is called the knot value for \(x_1\). The \(x_2\) variable is defined as a value of 1 when \(x_1 > k\) and a value of 0 when \(x_1 \le k\). With \(x_2\) defined this way, when \(x_1 \le k\), the equation becomes \(y = \beta_0 + \beta_1x_1 + \varepsilon\). When \(x1 > k\), the equation gets a new intercept and slope: \(y = (\beta_0 - k\beta_2) + (\beta_1 + \beta_2)x_1 + \varepsilon\).
Piecewise linear regression is built with typical linear regression functions with only some creation of new variables. In R, we can use the lm function on this cement data set. We are predicting STRENGTH using the RATIO variable as well the X2STAR variable which is \((x_1 - k)x_2\).
Code
cement.lm <-lm(STRENGTH ~ RATIO + X2STAR, data = cement)summary(cement.lm)
Call:
lm(formula = STRENGTH ~ RATIO + X2STAR, data = cement)
Residuals:
Min 1Q Median 3Q Max
-0.72124 -0.09753 -0.00163 0.24297 0.49393
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.79198 0.67696 11.510 7.62e-09 ***
RATIO -0.06633 0.01123 -5.904 2.89e-05 ***
X2STAR -0.10119 0.02812 -3.598 0.00264 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3286 on 15 degrees of freedom
Multiple R-squared: 0.9385, Adjusted R-squared: 0.9303
F-statistic: 114.4 on 2 and 15 DF, p-value: 8.257e-10
Code
ggplot(cement, aes(x = RATIO, y = STRENGTH)) +geom_point() +geom_line(data = cement, aes(x = RATIO, y = cement.lm$fitted.values)) +ylim(0,6)
We can see in the plot above how at the knot value of 70, the slope and intercept of the regression line changes.
The previous example dealt with piecewise functions that are continuous - the lines stay attached. However, you could make a small adjustment to the model to make the linear discontinuous:
With the addition of the same \(x_2\) variable as previously defined on its own instead of attached to the \((x_1-k)\) piece, the lines are no longer attached.
Code
cement.lm <-lm(STRENGTH ~ RATIO + X2STAR + X2, data = cement)summary(cement.lm)
Call:
lm(formula = STRENGTH ~ RATIO + X2STAR + X2, data = cement)
Residuals:
Min 1Q Median 3Q Max
-0.53167 -0.15513 0.06171 0.17239 0.49451
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.04975 0.68558 10.283 6.6e-08 ***
RATIO -0.05240 0.01174 -4.463 0.000536 ***
X2STAR -0.07888 0.02686 -2.937 0.010830 *
X2 -0.60388 0.26877 -2.247 0.041302 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2916 on 14 degrees of freedom
Multiple R-squared: 0.9548, Adjusted R-squared: 0.9451
F-statistic: 98.57 on 3 and 14 DF, p-value: 1.188e-09
Code
qplot(RATIO, STRENGTH, group = X2, geom =c('point', 'smooth'), method ='lm', data = cement, ylim =c(0,6))
Piecewise linear regression is built with typical linear regression functions with only some creation of new variables. In Python, we can use the ols function from statsmodels.formula.api on this cement data set. We are predicting STRENGTH using the RATIO variable as well the X2STAR variable which is \((x_1-k)x_2\).
Code
import statsmodels.formula.api as smffrom matplotlib import pyplot as pltimport seaborn as snscement_lm = smf.ols("STRENGTH ~ RATIO + X2STAR", data = cement).fit()cement_lm.summary()
OLS Regression Results
Dep. Variable:
STRENGTH
R-squared:
0.938
Model:
OLS
Adj. R-squared:
0.930
Method:
Least Squares
F-statistic:
114.4
Date:
Fri, 25 Oct 2024
Prob (F-statistic):
8.26e-10
Time:
13:50:02
Log-Likelihood:
-3.8688
No. Observations:
18
AIC:
13.74
Df Residuals:
15
BIC:
16.41
Df Model:
2
Covariance Type:
nonrobust
coef
std err
t
P>|t|
[0.025
0.975]
Intercept
7.7920
0.677
11.510
0.000
6.349
9.235
RATIO
-0.0663
0.011
-5.904
0.000
-0.090
-0.042
X2STAR
-0.1012
0.028
-3.598
0.003
-0.161
-0.041
Omnibus:
1.877
Durbin-Watson:
2.303
Prob(Omnibus):
0.391
Jarque-Bera (JB):
1.074
Skew:
-0.597
Prob(JB):
0.585
Kurtosis:
2.930
Cond. No.
582.
Notes: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
We can see in the plot above how at the knot value of 70, the slope and intercept of the regression line changes.
The previous example dealt with piecewise functions that are continuous - the lines stay attached. However, you could make a small adjustment to the model to make the linear discontinuous:
With the addition of the same \(x_2\) variable as previously defined on its own instead of attached to the \((x_1-k)\) piece, the lines are no longer attached.
Code
cement_lm = smf.ols("STRENGTH ~ RATIO + X2STAR + X2", data = cement).fit()cement_lm.summary()
OLS Regression Results
Dep. Variable:
STRENGTH
R-squared:
0.955
Model:
OLS
Adj. R-squared:
0.945
Method:
Least Squares
F-statistic:
98.57
Date:
Fri, 25 Oct 2024
Prob (F-statistic):
1.19e-09
Time:
13:50:03
Log-Likelihood:
-1.0976
No. Observations:
18
AIC:
10.20
Df Residuals:
14
BIC:
13.76
Df Model:
3
Covariance Type:
nonrobust
coef
std err
t
P>|t|
[0.025
0.975]
Intercept
7.0498
0.686
10.283
0.000
5.579
8.520
RATIO
-0.0524
0.012
-4.463
0.001
-0.078
-0.027
X2STAR
-0.0789
0.027
-2.937
0.011
-0.136
-0.021
X2
-0.6039
0.269
-2.247
0.041
-1.180
-0.027
Omnibus:
0.555
Durbin-Watson:
2.336
Prob(Omnibus):
0.758
Jarque-Bera (JB):
0.446
Skew:
-0.340
Prob(JB):
0.800
Kurtosis:
2.634
Cond. No.
678.
Notes: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Although the plot above looks like the line pieces are attached, that is just the visualization of the plot itself. There is no prediction between the two lines.
The piecewise linear regression equation can be extended to have as many pieces as you want. An example with three lines (two knots) is as follows:
One of the problems with this structure is that we have to define the knot values ourselves. The next set of models can help do that for us!
MARS (and EARTH)
Multivariate adaptive regression splines (MARS) is a non-parametric technique that still has a linear form to the model (additive) but has nonlinearities and interaction between variables. Essentially, MARS uses piecewise regression approach to split into pieces then potentially uses either linear or nonlinear patterns for each piece.
MARS first looks for the point in the range of a predictor \(x_i\) where two linear functions on either side of the point provides the least squared error (linear regression).
The algorithm continues on each piece of the piecewise function until many knots are found.
Example of Growing Number of Knots
This will eventually overfit your data. However, the algorithm then works backwards to “prune” (or remove) the knots that do not contribute significantly to out of sample accuracy. This out of sample accuracy calculation is performed by using the generalized cross-validation (GCV) procedure - a computational short-cut for leave-one-out cross-validation. The algorithm does this for all of the variables in the data set and combines the outcomes together.
The actual MARS algorithm is trademarked by Salford Systems, so instead the common implementation in most softwares is enhanced adaptive regression through hinges - called EARTH.
Let’s see how to do this in each of our softwares!
Let’s go back to our Ames housing data set and the variables we were working with in the previous section. One of the variables in our data set is Garage_Area. It doesn’t have a straight-forward relationship with our target variable Sale_Price as seen by the plot below.
Code
ggplot(training, aes(x = Garage_Area, y = Sale_Price)) +geom_point()
Let’s fit the EARTH algorithm between Garage_Area and Sale_Price. In the earth package is the earth function. The input is similar to most modeling functions in R, a formula to relate predictor variables to a target variable and an option to define the data set being used. We will then look at a summary of the output.
Code
library(earth)mars1 <-earth(Sale_Price ~ Garage_Area, data = training)summary(mars1)
Call: earth(formula=Sale_Price~Garage_Area, data=training)
coefficients
(Intercept) 124159.039
h(286-Garage_Area) -60.257
h(Garage_Area-286) 297.277
h(Garage_Area-521) -483.642
h(Garage_Area-576) 733.859
h(Garage_Area-758) -356.460
h(Garage_Area-1043) -490.873
Selected 7 of 7 terms, and 1 of 1 predictors
Termination condition: RSq changed by less than 0.001 at 7 terms
Importance: Garage_Area
Number of terms at each degree of interaction: 1 6 (additive model)
GCV 3427475346 RSS 6.94092e+12 GRSq 0.4492014 RSq 0.4556309
From the output above we see 6 pieces of the function defined by 5 knots. Those five knots correspond to the Garage_Area - ___ values above. The coefficients attached to each of those pieces are the same as what we would have in piecewise linear regression. The bottom of the output also shows the generalized \(R^2\) value as well as the typical \(R^2\) value.
To visualize the piecewise relationship between Garage_Area and Sale_Price we can plot the predicted values on the scatterplot from above.
Code
ggplot(training, aes(x = Garage_Area, y = Sale_Price)) +geom_point() +geom_line(data = training, aes(x = Garage_Area, y = mars1$fitted.values), color ="blue")
We can see that the Sale_Price of the home stays relative steady for small values of Garage_Area but then increases to a point, before it begins to level off again.
Now let’s build the algorithm on all the variables in the data set that we have. The Sale_Price ~ . notation tells the earth function to use all the variables in the data set to predict the Sale_Price.
Code
mars2 <-earth(Sale_Price ~ ., data = training)summary(mars2)
Call: earth(formula=Sale_Price~., data=training)
coefficients
(Intercept) 319493.46
Central_AirY 20289.49
h(4-Bedroom_AbvGr) 9214.66
h(Bedroom_AbvGr-4) -23009.05
h(Year_Built-1977) 1275.57
h(2004-Year_Built) -336.64
h(Year_Built-2004) 5315.57
h(13869-Lot_Area) -2.09
h(Lot_Area-13869) 0.22
h(First_Flr_SF-1600) 104.91
h(2402-First_Flr_SF) -71.56
h(First_Flr_SF-2402) -176.61
h(1523-Second_Flr_SF) -53.13
h(Second_Flr_SF-1523) 426.63
h(Half_Bath-1) -45378.31
h(2-Fireplaces) -14408.56
h(Fireplaces-2) -26072.58
h(Garage_Area-539) 101.97
h(Garage_Area-1043) -294.30
h(Gr_Liv_Area-2049) 65.21
h(Gr_Liv_Area-3194) -159.79
Selected 21 of 24 terms, and 10 of 14 predictors
Termination condition: Reached nk 29
Importance: First_Flr_SF, Second_Flr_SF, Year_Built, Garage_Area, ...
Number of terms at each degree of interaction: 1 20 (additive model)
GCV 1033819964 RSS 2.036439e+12 GRSq 0.8338641 RSq 0.8402842
Now that all of the variables have been added in, we see a lot of them remaining in the model to predict Sale_Price. There are knot values defined for all of the variables that are in the model. Right below the knot values in the output above we see that only 10 of the 14 original variables were used in the final model. Two lines below that we see variables listed by importance. We will look at this more below. Not surprisingly, the \(R^2\) and generalized \(R^2\) has increased with the addition of all these new variables. Notice how Garage_Area has different knot values then when we ran the algorithm on Garage_Area alone. That is because the algorithm prunes the knots with all of the variables in the model. Apparently, some of the other variables being in the model means we don’t need as many knots in the Garage_Area variable.
Let’s talk more about that variable importance metric in the above output. For each model size (1 term, 2 terms, etc.) there is one “subset” model - the best model for that size. EARTH ranks variables by how many of these “best models” of each size that variable appears in. The more subsets (or “best models”) that a variable appears in, the more important the variable. We can get this full output using the evimp function on our earth model object.
The nsubsets above is the number of subsets that the variable appears in. The rss above stands for residual sum of squares (or sum of squares error) is a scaled version of the decrease in residual sum of squares relative to the previous subset. Since it is scaled, the top variable always has a value of 100 while the remaining ones decrease from there. The gcv value is an approximation of rss on leave-one-out cross-validation and is also scaled.
At the writing of these notes, there was not a stable version of the MARS / EARTH algorithm that worked in the latest versions of numpy and scipy. The py-earth contributed package for scikit-learn has not been updated since 2017.
Interpretability of relationships between predictor variables and the target variable starts to get more complicated with the EARTH (or MARS) algorithm. You can plot the relationship as we see above, but those relationships can still be rather complicated and hard to explain to a client.
Smoothing
Generalized additive models can be made up of any non-parametric function of the predictor variables. Another popular technique is to use smoothing functions so the piecewise linear regressions are not so jagged. The following are different types of smoothing functions:
LOESS (localized regression)
Smoothing splines & regression splines
LOESS
Locally estimated scatterplot smoothing (LOESS) is a popular smoothing technique. The idea of LOESS is to perform weighted linear regression in small windows of a scatterplot of data between two variables. This weighted linear regression is done around each point as the window moves from the low end of the scatterplot values to the high end. An example is shown below:
LOESS Regression
The predictions of the these regression lines in each window are connected together to form the smoothed curve through the scatterplot as shown above.
Smoothing Splines
Smoothing splines take a different approach as compared to LOESS. Smoothing splines have a knot at every single observation for piecewise regression which leads to overfitting. There is a penalty parameter used to counterbalance the “wiggle” of the spline curve.
Smoothing splines try to find the function \(s(x_i)\) that optimally fits \(x_i\) to the target variable through the following equation:
By thinking of \(s(x_i)\) as a prediction of \(y\), the front half of the equation is equal to the sum of squared errors in your model. The second half of the equation above has the \(\lambda\) penalty applied to the integral of the second derivative of the smoothing function. To conceptually think of this second derivative we can think of it as the “slope of slopes” which is large when the curve has a lot of “wiggle”. The optimal value of the \(\lambda\) penalty is estimated with another approximation of leave-one-out cross-validation.
Regression splines are just a computationally nicer version of smoothing splines so they will not be covered in detail here.
Let’s see how to do GAM’s with splines in each of our softwares!
Continuing to use our Ames housing data set, we will build a gam using the mgcv package in R. Similar to previous functions the inputs are the formula for the model and the data = option to define the data set. We will also use the summary function to view the output. Inside of the formula, we use the s function to inform the gam function to which variables should have splines fit to them.
Code
library(mgcv)gam1 <- mgcv::gam(Sale_Price ~s(Garage_Area), data = training)summary(gam1)
From the output above we see two different sections - a section for coefficients that are not involved in splines and a section for smoothing terms. The p-value attached to the spline of Garage_Area shows the significance of that variable to the model as a whole. Similar to the EARTH algorithm, we can view a plot of the relationship between the variable and its predictions of the target. Here we use the plot function on the gam model object.
Code
plot(gam1)
This nonlinear and complex relationship between Garage_Area and Sale_Price is similar to the plot we saw earlier with EARTH. This shouldn’t be too surprising. Both algorithms are trying to relate these two variables together, just in different ways.
Let’s build out a GAM with all of the variables in our data set. The categorical variables are entered as either character variables or with the factor function. The continuous variables are defined with the spline function s.
Code
gam2 <- mgcv::gam(Sale_Price ~s(Bedroom_AbvGr, k =5) +s(Year_Built) +s(Mo_Sold) +s(Lot_Area) +s(First_Flr_SF) +s(Second_Flr_SF) +s(Garage_Area) +s(Gr_Liv_Area) +s(TotRms_AbvGrd) + Street + Central_Air +factor(Fireplaces) +factor(Full_Bath) +factor(Half_Bath) , method ='REML', data = training)summary(gam2)
The top half of the output has the variables not in splines, while the bottom half has the spline variables.
There are some variables with high p-values that could be removed from the model. One of the benefits of the gam function from the mgcv package is the select option. If we set select = TRUE then the model will penalize variables’ edf values. You can think of an edf value almost like a polynomial term. The selection technique will zero out this edf value - essentially, zeroing out the variable itself.
An example is shown below where the Mo_Sold variable is essentially zeroed from the model.
Code
sel.gam2 <- mgcv::gam(Sale_Price ~s(Bedroom_AbvGr, k =5) +s(Year_Built) +s(Mo_Sold) +s(Lot_Area) +s(First_Flr_SF) +s(Second_Flr_SF) +s(Garage_Area) +s(Gr_Liv_Area) +s(TotRms_AbvGrd) + Street + Central_Air +factor(Fireplaces) +factor(Full_Bath) +factor(Half_Bath) , method ='REML', select =TRUE, data = training)summary(sel.gam2)
Continuing to use our Ames housing data set, we will build a GAM using the GLMGam and BSplines functions from the stasmodels.gam.api package in Python. Similar to previous functions the inputs are the formula for the model and the data = option to define the data set. We will also use the smoother option to let the GLMGam function know which variables are being splined. The BSplines function used as an input to the GLMGam function is where we define the variables we want splined and to what degree we are splining them.
From the output above we see the p-values attached to the spline values of Garage_Area shows the significance of that variable to the model as a whole. Similar to the EARTH algorithm, we can view a plot of the relationship between the variable and its predictions of the target. Here we use the plot function on the gam model object.
Let’s build out a GAM with all of the variables in our data set. The categorical variables are entered as either character variables or with the C function. The continuous variables are defined with the spline function BSplines.
The top half of the output has the variables not in splines, while the bottom half has the spline variables. There are some variables with high p-values that could be removed from the model.
Summary
In summary, GAM’s are good models to use for prediction, but explanation becomes more difficult and complex. Some of the advantages of using GAM’s:
Allows nonlinear relationships without trying out many transformations manually
Improved predictions
Limited “interpretation” still available
Computationally fast for small numbers of variables
There are some disadvantages though:
Interactions are possible, but computationally intensive
Not good for large number of variables so prescreening is needed
---title: "Generalized Additive Models"format: html: code-fold: show code-tools: trueeditor: visual---```{r}#| warning: false#| include: false#| error: false#| message: falselibrary(AmesHousing)ames <-make_ordinal_ames()library(tidyverse)ames <- ames %>%mutate(id =row_number())set.seed(4321)training <- ames %>%sample_frac(0.7)testing <-anti_join(ames, training, by ='id')training <- training %>%select(Sale_Price, Bedroom_AbvGr, Year_Built, Mo_Sold, Lot_Area, Street, Central_Air, First_Flr_SF, Second_Flr_SF, Full_Bath, Half_Bath, Fireplaces, Garage_Area, Gr_Liv_Area, TotRms_AbvGrd)``````{python}#| include: false#| warning: false#| error: false#| message: falsetraining = r.trainingtesting = r.testing```# General StructureGeneralized Additive Models (GAM's) provide a general framework for adding of non-linear functions together instead of the typical linear structure of linear regression. GAM's can be used for either continuous or categorical target variables. The structure of GAM's are the following:$$y = \beta_0 + f_1(x_1) + \cdots + f_p(x_p) + \varepsilon$$The $f_i(x_i)$ functions are complex, nonlinear functions on the predictor variables. GAM's add these complex, yet individual functions together. This allows for many complex relationships to try and model with to potentially predict your target variable better. We will examine a few different forms of GAM's below.# Piecewise Linear RegressionThe slope of the linear relationship between a predictor variable and a target variable can change over different values of the predictor variable. The typical straight-line model $\hat{y} = \beta_0 + \beta_1x_1$ will not be a good fit for this type of data.Here is an example of a data set that exhibits this behavior - comprehensive strength of concrete and the proportion of water mixed with cement. The comprehensive strength decreases at a much faster rate for batches with a greater than 70% water/cement ratio.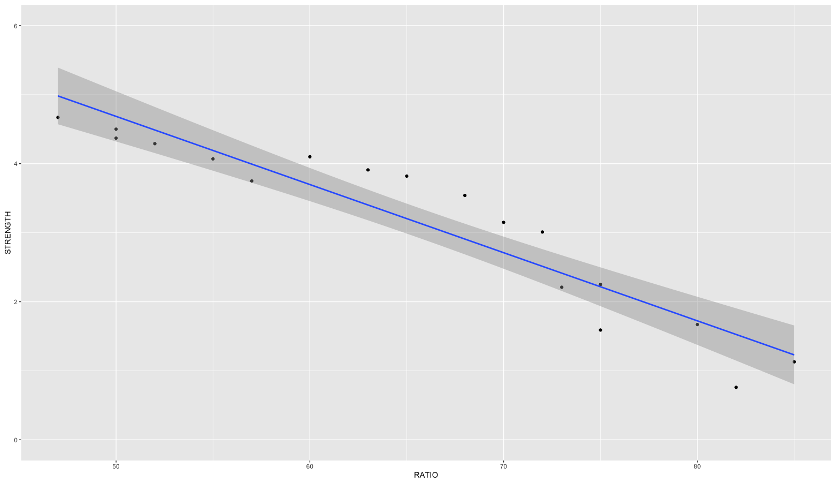{fig-align="center" width="6in"}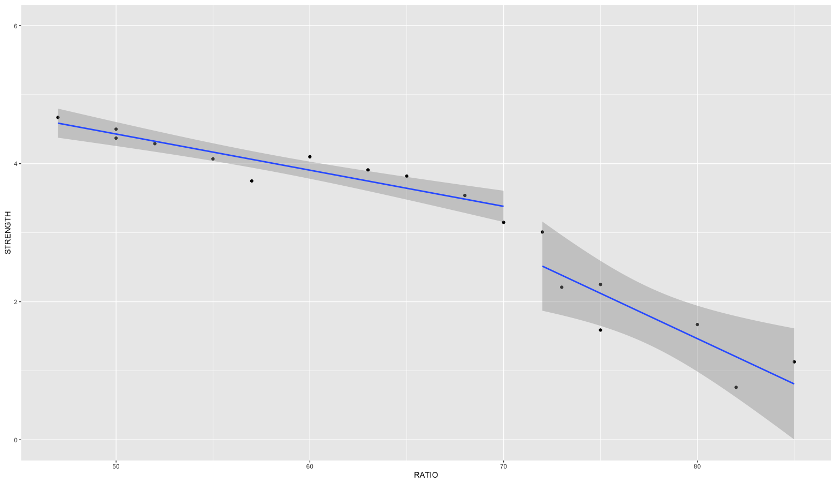{fig-align="center" width="6in"}If you were to fit a linear regression as the first image above, it wouldn't represent the data very well. However, this is perfect for a **piecewise linear regression**. Piecewise linear regression is a model where there are different straight-line relationships for different intervals in the predictor variable. The following piecewise linear regression is for two slopes:$$y = \beta_0 + \beta_1x_1 + \beta_2(x_1-k)x_2 + \varepsilon$$The $k$ value in the equation above is called the **knot value** for $x_1$. The $x_2$ variable is defined as a value of 1 when $x_1 > k$ and a value of 0 when $x_1 \le k$. With $x_2$ defined this way, when $x_1 \le k$, the equation becomes $y = \beta_0 + \beta_1x_1 + \varepsilon$. When $x1 > k$, the equation gets a new intercept and slope: $y = (\beta_0 - k\beta_2) + (\beta_1 + \beta_2)x_1 + \varepsilon$.Let's see this in each of our softwares!::: {.panel-tabset .nav-pills}## RPiecewise linear regression is built with typical linear regression functions with only some creation of new variables. In R, we can use the `lm` function on this cement data set. We are predicting `STRENGTH` using the `RATIO` variable as well the `X2STAR` variable which is $(x_1 - k)x_2$.```{r}#| warning: false#| error: false#| message: false#| include: falsecement <-read.csv("data/cement.csv", header =TRUE)``````{r}#| warning: false#| error: false#| message: falsecement.lm <-lm(STRENGTH ~ RATIO + X2STAR, data = cement)summary(cement.lm)ggplot(cement, aes(x = RATIO, y = STRENGTH)) +geom_point() +geom_line(data = cement, aes(x = RATIO, y = cement.lm$fitted.values)) +ylim(0,6)```We can see in the plot above how at the knot value of 70, the slope and intercept of the regression line changes.The previous example dealt with piecewise functions that are continuous - the lines stay attached. However, you could make a small adjustment to the model to make the linear discontinuous:$$y = \beta_0 + \beta_1x_1 + \beta_2(x_1 - k)x_2 + \beta_3x_2 + \varepsilon$$With the addition of the same $x_2$ variable as previously defined on its own instead of attached to the $(x_1-k)$ piece, the lines are no longer attached.```{r}#| warning: false#| error: false#| message: falsecement.lm <-lm(STRENGTH ~ RATIO + X2STAR + X2, data = cement)summary(cement.lm)qplot(RATIO, STRENGTH, group = X2, geom =c('point', 'smooth'), method ='lm', data = cement, ylim =c(0,6))```## Python```{python}#| warning: false#| error: false#| message: false#| include: falsecement = r.cement```Piecewise linear regression is built with typical linear regression functions with only some creation of new variables. In Python, we can use the `ols` function from `statsmodels.formula.api` on this cement data set. We are predicting `STRENGTH` using the `RATIO` variable as well the `X2STAR` variable which is $(x_1-k)x_2$.```{python}#| warning: false#| error: false#| message: falseimport statsmodels.formula.api as smffrom matplotlib import pyplot as pltimport seaborn as snscement_lm = smf.ols("STRENGTH ~ RATIO + X2STAR", data = cement).fit()cement_lm.summary()plt.cla()fig, ax = plt.subplots(figsize=(6, 4))sns.scatterplot(x ='RATIO', y='STRENGTH', data = cement, ax = ax)x_pred = cement['RATIO']y_pred = cement_lm.fittedvaluessns.lineplot(x = x_pred, y = y_pred, ax = ax)plt.show()```We can see in the plot above how at the knot value of 70, the slope and intercept of the regression line changes.The previous example dealt with piecewise functions that are continuous - the lines stay attached. However, you could make a small adjustment to the model to make the linear discontinuous:$$y = \beta_0 + \beta_1x_1 + \beta_2(x_1-k)x_2 + \beta_3x_2 + \varepsilon$$With the addition of the same $x_2$ variable as previously defined on its own instead of attached to the $(x_1-k)$ piece, the lines are no longer attached.```{python}#| warning: false#| error: false#| message: falsecement_lm = smf.ols("STRENGTH ~ RATIO + X2STAR + X2", data = cement).fit()cement_lm.summary()plt.cla()fig, ax = plt.subplots(figsize=(6, 4))sns.scatterplot(x ='RATIO', y='STRENGTH', data = cement, ax = ax)x_pred = cement['RATIO']y_pred = cement_lm.fittedvaluessns.lineplot(x = x_pred, y = y_pred, ax = ax)plt.show()```Although the plot above looks like the line pieces are attached, that is just the visualization of the plot itself. There is no prediction between the two lines.:::The piecewise linear regression equation can be extended to have as many pieces as you want. An example with three lines (two knots) is as follows:$$y = \beta_0 +\beta_1x_1 + \beta_2(x_1-k_1)x_2 + \beta_3(x_1-k_2)x_3 + \varepsilon$$One of the problems with this structure is that we have to define the knot values ourselves. The next set of models can help do that for us!# MARS (and EARTH)Multivariate adaptive regression splines (MARS) is a non-parametric technique that still has a linear form to the model (additive) but has nonlinearities and interaction between variables. Essentially, MARS uses piecewise regression approach to split into pieces then potentially uses either linear or nonlinear patterns for each piece.MARS first looks for the point in the range of a predictor $x_i$ where two linear functions on either side of the point provides the least squared error (linear regression).```{r}#| echo: false#| warning: false#| error: false#| message: falsecement.lm <-lm(STRENGTH ~ RATIO + X2STAR, data = cement)ggplot(cement, aes(x = RATIO, y = STRENGTH)) +geom_point() +geom_line(data = cement, aes(x = RATIO, y = cement.lm$fitted.values)) +ylim(0,6)```The algorithm continues on each piece of the piecewise function until many knots are found.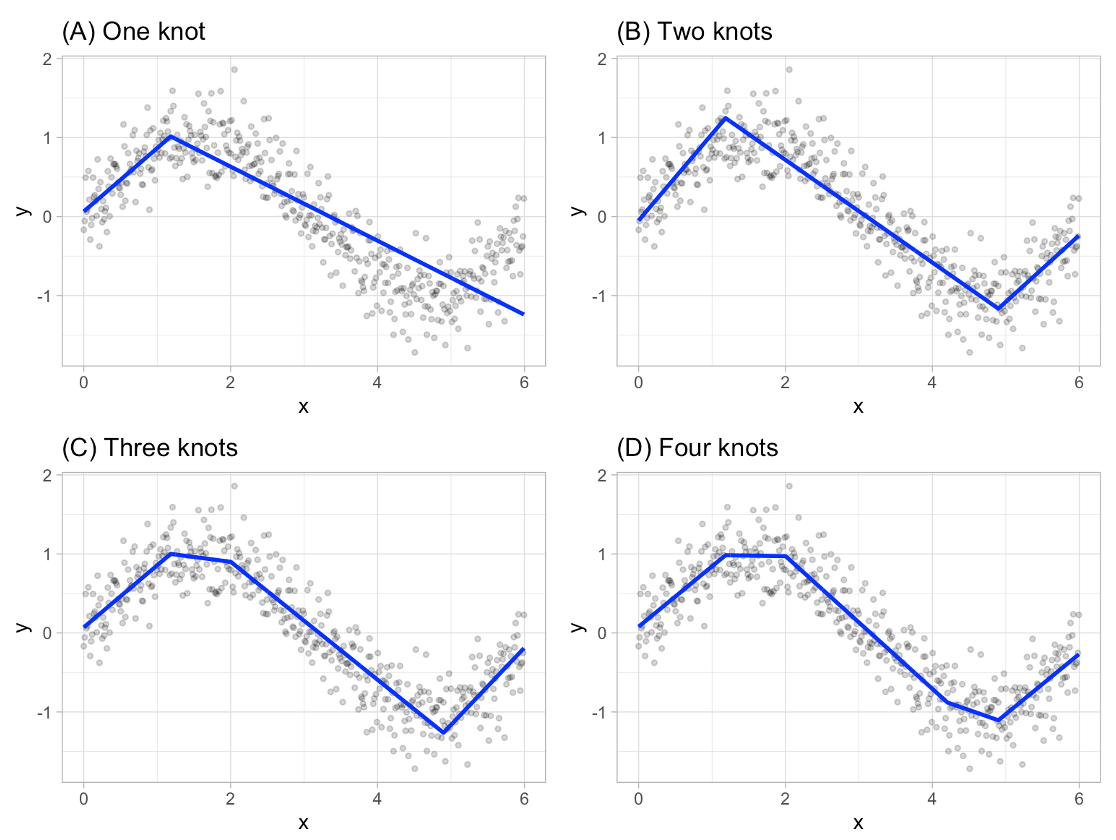{fig-align="center" width="6in"}This will eventually overfit your data. However, the algorithm then works backwards to "prune" (or remove) the knots that do not contribute significantly to out of sample accuracy. This out of sample accuracy calculation is performed by using the **generalized cross-validation** (GCV) procedure - a computational short-cut for leave-one-out cross-validation. The algorithm does this for all of the variables in the data set and combines the outcomes together.The actual MARS algorithm is trademarked by Salford Systems, so instead the common implementation in most softwares is **enhanced adaptive regression through hinges** - called EARTH.Let's see how to do this in each of our softwares!::: {.panel-tabset .nav-pills}## RLet's go back to our Ames housing data set and the variables we were working with in the previous section. One of the variables in our data set is `Garage_Area`. It doesn't have a straight-forward relationship with our target variable `Sale_Price` as seen by the plot below.```{r}#| warning: false#| error: false#| message: falseggplot(training, aes(x = Garage_Area, y = Sale_Price)) +geom_point()```Let's fit the EARTH algorithm between `Garage_Area` and `Sale_Price`. In the `earth` package is the `earth` function. The input is similar to most modeling functions in R, a formula to relate predictor variables to a target variable and an option to define the data set being used. We will then look at a `summary` of the output.```{r}#| warning: false#| error: false#| message: falselibrary(earth)mars1 <-earth(Sale_Price ~ Garage_Area, data = training)summary(mars1)```From the output above we see 6 pieces of the function defined by 5 knots. Those five knots correspond to the `Garage_Area - ___` values above. The coefficients attached to each of those pieces are the same as what we would have in piecewise linear regression. The bottom of the output also shows the generalized $R^2$ value as well as the typical $R^2$ value.To visualize the piecewise relationship between `Garage_Area` and `Sale_Price` we can plot the predicted values on the scatterplot from above.```{r}#| warning: false#| error: false#| message: falseggplot(training, aes(x = Garage_Area, y = Sale_Price)) +geom_point() +geom_line(data = training, aes(x = Garage_Area, y = mars1$fitted.values), color ="blue")```We can see that the `Sale_Price` of the home stays relative steady for small values of `Garage_Area` but then increases to a point, before it begins to level off again.Now let's build the algorithm on all the variables in the data set that we have. The `Sale_Price ~ .` notation tells the `earth` function to use all the variables in the data set to predict the `Sale_Price`.```{r}#| warning: false#| error: false#| message: falsemars2 <-earth(Sale_Price ~ ., data = training)summary(mars2)```Now that all of the variables have been added in, we see a lot of them remaining in the model to predict `Sale_Price`. There are knot values defined for all of the variables that are in the model. Right below the knot values in the output above we see that only 10 of the 14 original variables were used in the final model. Two lines below that we see variables listed by importance. We will look at this more below. Not surprisingly, the $R^2$ and generalized $R^2$ has increased with the addition of all these new variables. Notice how `Garage_Area` has different knot values then when we ran the algorithm on `Garage_Area` alone. That is because the algorithm prunes the knots with all of the variables in the model. Apparently, some of the other variables being in the model means we don't need as many knots in the `Garage_Area` variable.Let's talk more about that variable importance metric in the above output. For each model size (1 term, 2 terms, etc.) there is one "subset" model - the best model for that size. EARTH ranks variables by how many of these "best models" of each size that variable appears in. The more subsets (or "best models") that a variable appears in, the more important the variable. We can get this full output using the `evimp` function on our `earth` model object.```{r}#| warning: false#| error: false#| message: falseevimp(mars2)```The `nsubsets` above is the number of subsets that the variable appears in. The `rss` above stands for residual sum of squares (or sum of squares error) is a scaled version of the decrease in residual sum of squares relative to the previous subset. Since it is scaled, the top variable always has a value of 100 while the remaining ones decrease from there. The `gcv` value is an approximation of `rss` on leave-one-out cross-validation and is also scaled.## Python```{python}#| warning: false#| error: false#| message: false```At the writing of these notes, there was not a stable version of the MARS / EARTH algorithm that worked in the latest versions of `numpy` and `scipy`. The `py-earth` contributed package for `scikit-learn` has not been updated since 2017.:::Interpretability of relationships between predictor variables and the target variable starts to get more complicated with the EARTH (or MARS) algorithm. You can plot the relationship as we see above, but those relationships can still be rather complicated and hard to explain to a client.# SmoothingGeneralized additive models can be made up of any non-parametric function of the predictor variables. Another popular technique is to use **smoothing functions** so the piecewise linear regressions are not so jagged. The following are different types of smoothing functions:- LOESS (localized regression)- Smoothing splines & regression splines## LOESSLocally estimated scatterplot smoothing (LOESS) is a popular smoothing technique. The idea of LOESS is to perform weighted linear regression in small windows of a scatterplot of data between two variables. This weighted linear regression is done around each point as the window moves from the low end of the scatterplot values to the high end. An example is shown below:{fig-align="center" width="8in"}The predictions of the these regression lines in each window are connected together to form the smoothed curve through the scatterplot as shown above.## Smoothing SplinesSmoothing splines take a different approach as compared to LOESS. Smoothing splines have a knot at every single observation for piecewise regression which leads to overfitting. There is a penalty parameter used to counterbalance the "wiggle" of the spline curve.Smoothing splines try to find the function $s(x_i)$ that optimally fits $x_i$ to the target variable through the following equation:$$\min\sum_{i=1}^n (y_i - s(x_i))^2 + \lambda\int s''(t_i)^2 dt$$By thinking of $s(x_i)$ as a prediction of $y$, the front half of the equation is equal to the sum of squared errors in your model. The second half of the equation above has the $\lambda$ penalty applied to the integral of the second derivative of the smoothing function. To conceptually think of this second derivative we can think of it as the "slope of slopes" which is large when the curve has a lot of "wiggle". The optimal value of the $\lambda$ penalty is estimated with another approximation of leave-one-out cross-validation.Regression splines are just a computationally nicer version of smoothing splines so they will not be covered in detail here.Let's see how to do GAM's with splines in each of our softwares!::: {.panel-tabset .nav-pills}## RContinuing to use our Ames housing data set, we will build a `gam` using the `mgcv` package in R. Similar to previous functions the inputs are the formula for the model and the `data =` option to define the data set. We will also use the `summary` function to view the output. Inside of the formula, we use the `s` function to inform the `gam` function to which variables should have splines fit to them.```{r}#| warning: false#| error: false#| message: falselibrary(mgcv)gam1 <- mgcv::gam(Sale_Price ~s(Garage_Area), data = training)summary(gam1)```From the output above we see two different sections - a section for coefficients that are not involved in splines and a section for smoothing terms. The p-value attached to the spline of `Garage_Area` shows the significance of that variable to the model as a whole. Similar to the EARTH algorithm, we can view a plot of the relationship between the variable and its predictions of the target. Here we use the `plot` function on the `gam` model object.```{r}#| warning: false#| error: false#| message: falseplot(gam1)```This nonlinear and complex relationship between `Garage_Area` and `Sale_Price` is similar to the plot we saw earlier with EARTH. This shouldn't be too surprising. Both algorithms are trying to relate these two variables together, just in different ways.Let's build out a GAM with all of the variables in our data set. The categorical variables are entered as either character variables or with the `factor` function. The continuous variables are defined with the spline function `s`.```{r}#| warning: false#| error: false#| message: falsegam2 <- mgcv::gam(Sale_Price ~s(Bedroom_AbvGr, k =5) +s(Year_Built) +s(Mo_Sold) +s(Lot_Area) +s(First_Flr_SF) +s(Second_Flr_SF) +s(Garage_Area) +s(Gr_Liv_Area) +s(TotRms_AbvGrd) + Street + Central_Air +factor(Fireplaces) +factor(Full_Bath) +factor(Half_Bath) , method ='REML', data = training)summary(gam2)```The top half of the output has the variables not in splines, while the bottom half has the spline variables.There are some variables with high p-values that could be removed from the model. One of the benefits of the `gam` function from the `mgcv` package is the `select` option. If we set `select = TRUE` then the model will penalize variables' edf values. You can think of an edf value almost like a polynomial term. The selection technique will zero out this edf value - essentially, zeroing out the variable itself.An example is shown below where the `Mo_Sold` variable is essentially zeroed from the model.```{r}#| warning: false#| error: false#| message: falsesel.gam2 <- mgcv::gam(Sale_Price ~s(Bedroom_AbvGr, k =5) +s(Year_Built) +s(Mo_Sold) +s(Lot_Area) +s(First_Flr_SF) +s(Second_Flr_SF) +s(Garage_Area) +s(Gr_Liv_Area) +s(TotRms_AbvGrd) + Street + Central_Air +factor(Fireplaces) +factor(Full_Bath) +factor(Half_Bath) , method ='REML', select =TRUE, data = training)summary(sel.gam2)```## PythonContinuing to use our Ames housing data set, we will build a GAM using the `GLMGam` and `BSplines` functions from the `stasmodels.gam.api` package in Python. Similar to previous functions the inputs are the formula for the model and the `data =` option to define the data set. We will also use the `smoother` option to let the `GLMGam` function know which variables are being splined. The `BSplines` function used as an input to the `GLMGam` function is where we define the variables we want splined and to what degree we are splining them.```{python}#| warning: false#| error: false#| message: falseimport statsmodels as smfrom statsmodels.gam.api import GLMGam, BSplinesx_spline = training['Gr_Liv_Area']bs = BSplines(x_spline, df =5, degree =3)gam1 = GLMGam.from_formula('Sale_Price ~ C(Central_Air)', data = training, smoother = bs).fit()gam1.summary()```From the output above we see the p-values attached to the spline values of `Garage_Area` shows the significance of that variable to the model as a whole. Similar to the EARTH algorithm, we can view a plot of the relationship between the variable and its predictions of the target. Here we use the `plot` function on the `gam` model object.Let's build out a GAM with all of the variables in our data set. The categorical variables are entered as either character variables or with the `C` function. The continuous variables are defined with the spline function `BSplines`.```{python}#| warning: false#| error: false#| message: falsex_spline = training[['Gr_Liv_Area', 'Year_Built','Mo_Sold','Lot_Area','First_Flr_SF','Second_Flr_SF','Garage_Area','Gr_Liv_Area','TotRms_AbvGrd']]bs = BSplines(x_spline, df = [5, 5, 5, 5, 5, 5, 5, 5, 5], degree = [3, 3, 3, 3, 3, 3, 3, 3, 3])gam2 = GLMGam.from_formula('Sale_Price ~ C(Central_Air) + C(Fireplaces) + C(Street) + C(Full_Bath) + C(Half_Bath)', data = training, smoother = bs).fit()gam2.summary()```The top half of the output has the variables not in splines, while the bottom half has the spline variables. There are some variables with high p-values that could be removed from the model.:::# SummaryIn summary, GAM's are good models to use for prediction, but explanation becomes more difficult and complex. Some of the advantages of using GAM's:- Allows nonlinear relationships without trying out many transformations manually- Improved predictions- Limited "interpretation" still available- Computationally fast for small numbers of variablesThere are some disadvantages though:- Interactions are possible, but computationally intensive- Not good for large number of variables so prescreening is needed- Multicollinearity still a problem.